1.Перемикальні функції.
Всі цифрові пристрої побудовані на елементах, що виконують ті або інші логічні операції. Одні елементи забезпечують обробку цифрової інформації; інші - комутацію каналів по яких передається інформація; треті – управління, четверті - зберігання.
Електричні сигнали, що діють на входах і виходах цифрових елементів мають два різні рівні напруги електричних сигналів (наприклад 5 і 0 В)і можуть бути представлені двійковими символами 1 або 0.
Змінна
X, що приймає тільки два значення / 0 і 1
/, називається двійковою, логічною або
булевою змінною . Функція
двійкових змінних
,
також приймає тільки два значення / 0
і 1 /, і називається функцією перемикача
або булевою функцією, або функцією
алгебри логіки. Тобто булева
функція - двійкова функція двійкового
аргументу.
Булева функція, що залежить від п аргументів, називається п-місною і є повністю визначеною, якщо вказані її значення для всіх двійкових наборів аргументів. Число таких наборів залежить від числа змінних п і дорівнює 2n.
Якщо булева функція визначена не на всіх наборах, то вона є неповністю визначеною або недовизначеною.
Функції перемикачів бувають комбінаційними і тимчасовими.
2.Закони та правила алгебри логіки.
В алгебрі логіки є чотири основні закони:
1. Закон перестановки (комутативний):
А+В =В+А - для диз'юнкції; АВ=ВА - для кон'юнкції.
2. Сполучний (асоціативний)
А+(В+С)=(А+В)+С
А(ВС)=(АВ)С
3. Розподільний (дистрибутивний)
А+ВС=(А+В)(А+С)
А(В+С)=АВ+АС
4. Інверсія (правило де Моргана)
;
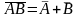
Використовуючи основні закони алгебри логіки можна скласти ряд правил, які застосовуються при аналізі складних логічних виразів:
1.Інверсія:
2. Правила операцій з константами:
А+0=а; А*1=а - правило незмінності А+1=1; А*0=0
3.Повторення (ідемпотентності)
А+А=А
А*А=А
4. Поглинання (надмірності)
А + АВ = А А(1 + В) = А
А (А+В) = А АА + АВ = А + АВ = А (1 + В) = А
5.Доповнення
6. Склеювання (узгодження)
7. Подвійне заперечення ( подвійна інверсія)
3.Поняття про комбінаційні та часові функції
Функції перемикачів бувають комбінаційними і тимчасовими.
Комбінаційними називаються функції, значення яких однозначно визначаються значеннями їх аргументів. Ці функції часто називають функціями без пам'яті, оскільки вони не володіють властивостями запам'ятовування інформації. Попередні значення аргументів і функцій не впливають на формування нового значення функції при новому наборі аргументів.
Схеми, які реалізують комбінаційні функції називаються комбінаційними.
Тимчасовими називаються функції, значення яких визначаються не тільки даним набором аргументів, але і минулими значеннями аргументів або функцій. При одних і тих же значеннях аргументів значення тимчасової функції може бути різним. Тимчасові функції іноді називають функціями з пам'яттю, оскільки вони володіють властивостями запам'ятовування інформації.
Комбінаційна логічна функція може бути задана словесно, таблицею або виразом алгебри.