1. Металл жүйелерге арналған атомаралық потенциалдар

Металл жүйелердегі байланыстар 0,2-0,5ϕ[нм] атомаралық қашықтық шектерінде түзіледі. Үлкен атомаралық қашықтықтарда ұзақтан әсер ету байланыстарына жауапты Ван-дер-Вальс күштері жүреді. Металдық байланыстар ковалентті байланыстар сияқты электрондарды ортақ қолдану нәтижесінде пайда болады, яғни металдық байланыстарды сипаттау көптік бөлшектің өзара әсерлесу эффектілерін ескеруді талап етеді. Екі бөлшектік потенциалдар көмегімен бұл байланыстарды сипаттау мүмкін емес, себебі

а) кубикті торы бар көптеген металдар үшін С₁₂ серпімділік тұрақтысының С₄₄ серпімділік тұрақтысына қатынасы 1-ден өзгеше, ал жұптық потенциал Коши қатынасына алып келеді, яғни C₁₂ = C₄₄;

б) релаксацияланбаған орын пішімделуінің алдын ала есептелген энергиясы когезиондық энергия мәніне жақын, ал бұл металдар үшін мүлде орынсыз (сәйкес емес); металдардың релаксация энергиясы өте кішкентай. Тәжірибелік мәліметтер металдардағы орынның (ваканция) түзілу энергиясы когезиондық энергия өлшемінің шамамен -ін құрайды.

в) теориялық бағалауларға сәйкес реконструкцияланбаған (қайта құрылмаған, өңделмеген) беткей құрылымының шегіндегі бірінші және екінші атомдық қабаттарының арасындағы атомаралық қашықтық жұптық потенциалдар арқасында артады. Бұл кристал торының ашық беткейінің сығылуын қарастыратын тәжірибелік мәліметтерге қарсы келеді, яғни жұптық өзара әсерлесу потенциалдары металл беткейлердің ішкі релаксациясын болжауға мүмкіндік бермейді.

г) жұптық потенциалдардың жақындауы балқу нүктесін тәжірибелік мәнге қарағанда 20% -ға арттырады;

д) екі атомның тең қашықтығына жауапты бір ғана оптимальді мәні бар функция формасы бар потенциалдар фондық жиіліктермен қажетті үйлесімді қамтамасыз ете алмайды. Жұптық потенциалдарды қолдану аясынан шығып, көпбөлшекті эффектілердің қосылуы үшін екібөлшекті өзара әссерлесу потенциалдарына екі тәсіл ұсынылған (қарастырылған).

Бірінші тәсіл – жұптық өзара әсерлесу қосылғышына локальді жақын берілген атомның электрондық тығыздығы функционалы түріндегі қосылғышты қосу. Бұл әдіс көпбөлшекті өзара әсерлесуге ұқсайтын бірнеше альтернативті потенциалдарға автоматты түрде әкелді. Бұл көпбқлшекті потенциалдар, «батырылған» атом моделі (МПА) потенциалдары ретінде де белгілі, олар элементар металдар мен олардың қорытпаларымен, «жабыспалы» модель потенциалдарымен, ОЦК-торы бар элементар металдарға арналған Финнис-Синклер потенциалдарымен, ОЦК-торы бар элементар металдарға арналған Саттон Чен (СЧ) потенциалымен, ГЦК- торы бар металдардың ретсіз бинарлық қорытпаларына арналған Рафий-Табар және Саттон потенциалдарымен жұмыс істеу кезінде және бірнеше модельдік зерттеулерде қолданылған.

Екінші тәсіл жоғарырақ реттік өзара әсерлесулерді енгізу, мысалы, сәйкес пішіні мен симметриясы бар үшбөлшекті немесе төртбөлшекті мүшелердің өзара әсерлесуін енгізу арқылы жұптық потенциалдан кластерлік потенциалдарға ауысу. Бұл Меррел-Моттрамм кластераралық потенциалдары текті потенциалдарға әкелді. Жоғарырақ реттік өзара әсерлесуді қарастыратын мүшелерді қосу, жұптық потенциалдарға қарағанда, құбылыстар энергиясының дәлірек өңделуін қамтамасыз етеді.

1. «Батырылған» атом моделінің көпбөлшекті потенциалдары (МПА). МПА көпбөлшекті потенциалдары металл кластерлердегі байланыстардың түзілуін өңдеу үшін ұсынылған. Бұл потенциалдар дәстүрлі жұптық потенциалдардың алғашқы альтернативті моделі болды. Олар тығыздық функционалы теориясының (ТФП) негізінде жасалған, оған сәйкес атомдардың жиынтық энергиясы олардағы электрондық тығыздық функционалымен дәл сипаттала алады. Осыған ұқсас, «еге» атомдары ортасына атомның «батуына» байланысты энергияның өзгеруі, «еге» атомдарындағы электрондық тығыздықтан өзге «батырылған» атомға дейінгі функционалы болып табылады. Егер біз атомның «бату» функционалына жақындау (ұқсау) тапсақ, онда металдағы атом энергиясына жақын (ұқсас) мән енгізуге болады.

«Еге» атомдарының толық электрондық тығыздығын «егенің» жеке атомдарының электрондық тығыздықтары функцияларының сызықтық суперпозициясымен (зарядтардың таралуы) аппросимирациялайды. Нольдік жақындау кезінде «бату» энергиясын біртекті электрондық газдағы «бату» атомы энергиясымен теңестіруге болады. Оның тығыздығы ρ_h,i , атомның «бату» орнындағы «еге» тығыздығымен салыстырмалы және «еге» атомдарымен классикалық электростатикалық өзара әсерлесуінің есебінен үлкейеді. Біртекті электрондық газға арналған «бату» энергиясын бірінші принциптер негізінде есептеуге болады. «Батырылған» атомның кеңістіктік ұзындығы шектеріндегі «еге» тығыздығының өлшенген орташа мәнінен ρ_h,i –ді есептеу, «еге» тығыздығының локальді біртекті еместілігін есептеудің арқасында формализмді жақсартады. Егер «егенің» әрбір атомы үшін «қатырылған» атомдық зарядтар тығыздығын қойса, онда классикалық электростатикалық өзара әсерлесужиынтығына айналады. Бұл тәсіл квазиатомдық әдіс немесе эффективті орта теориясы деп аталады және МПА мен ұқсас (аналогиялық) әдістерге теориялық негіз береді.

Сәйкесінше, МПА–да атомдық жүйенің ортақ энергиясы келесідей:

(11)

мұндағы ϕ енді атомдарына тәуелді. «Егенің» электрондық тығыздығы келесі байланыспен беріледі:

, (12)

қосындының әрбір қосылғышы көрші j атомының типіне тәуелді. Сондықтан А және В типті атомдары бар бинарлық қорытпаның МПА энергиясы үшін φ_АА(r), φ_ВВ(r), φ_АВ(r), ρ_А(r), ρ_В(r), F_А(ρ), F_В(ρ) өлшемдерін анықтау қажет.

2. Финнис және Синклердің (ФС) көпбөлшекті потенциалдары.Бұл потенциалдар алғашында өтпелі металдардың энергетикалық күйін өңдеу үшін жасалған. Олар металдарды өңдеуге арналған жұптық потенциалдарды қолдануға байланысты мәселерді реттейді, мысалы, кубикті кристалдар үшін жарамсыз С₁₂ = C₄₄ Коши байланысы түріндегі серпімділік тұрақтылары арасындағы өзара байланыстың пайда болуы.

ФС моделінде N атомы жүйесінің энергиясы келесі түрде болады:

(13)

мұндағы

(14)

функциясы қашықтықта орналасқан i және j атомдары арасындағы тебілуге сәйкес келетін жұптық өзара әсерлесуді сипаттайды, – екі бөлшектің тартылу энергиясын сипаттауға арналған жұптық потенциалдар және с – оң тұрақты. (13) теңдіктегі екінші мүше көпбөлшекті тартылудың энергияға үлесін көрсетеді. Бұл қосылғыштың квадраттық түбірі күшті байланыс моделіндегі екінші моменттердің жақындау аналогиясымен байланысты. Бұған көз жеткізу үшін күшті байланыс тәсілінен бастайық. Күшті байланыс тәсілінде электрондық зонаның толық энергиясы, яғни байланыстың түзілуінің бірэлектронды бос емес күйлер энергияларының қосындысы ретінде берілетін жалпы энергия келесі теңдік арқылы жазылады:

, (15)

- күйлердің электрондық тығыздығы, – Ферми деңгейінің энергиясы, 2 көбейткіші спиндік құлдырауды ескереді, – тартылу энергиясының конфигурациялық өзара әсерлесу энергиясына үлесі. Конфигурациялық өзара әсерлесу энергиясы қатты дене түзілу барысында атомдардың жартылай толтырылған валенттік қабығының зоналарға бөлінуіне байланысты басым (жоғарырақ) болады. – ді жеке атомдардың үлесіне бөлген жөн:

, (16)

онда

(17)

– i түйініндегі күйлердің мүмкін тығыздығы және – бірэлектронды гамильтонианның сәйкес толқындық функциясы. – нің тура мәндерін алу үшін кристалдағы барлық атомдардың орналасуын білу қажет. Сондай–ақ, осы атомдардың орналасу координаттарының күрделі функционалы. Дегенмен өлшемдердің Е_і сияқты ұқсас мәндерін табу үшін жақсы ойластырылған формасына үміттенудің қажеті шамалы. Е_і формасының интегралы болғандықтан, оны есептеу үшін олардың ұштараның ені мен форманың жалпы ерекшеліктері туралы мәліметтер ғана керек. Бұл ақпарат моменттерінде ыңғайлы қосылады және келесі формуламен анықталады:

(18)

Атомаралық потенциалдар сипаттамасымен салыстыруға болатын қарапайым сипаттама – берген моменттердің локальді ортамен дәл анықталатындығында. Дәл теңдікке жататындар:

(19)

,

мұндағы

, (20)

- i атомындағы ортамен локальденген орбиталь, Н – бір электронды гамильтониан. Яғни, егер – дің алғашқы бірнеше функциясы түріндегі ұқсас мәні болса, атомаралық потенциалдардағы бағалау үшін қолданылған, мәліметтерді өңдеу механизмдерінің көмегімен есептеуге болады. Енді – ді тура бағалау үшін і түйініндегі моменттерінің барлық мәндері қажет. Дегенмен көп ақпаратты екінші моментіне негізделген сипаттамадан алуға болады. Бұл момент валенттік зонаның квадраттық енінің өлшемін білдіреді, яғни осы мәселе үшін энергияның жалпы масштабын бекітеді. Сондықтын тек көмегімен жасалған сипаттама функциясының формасын ескермеуге болатындығын көрсетеді, себебі – ң жоғарғы моменттері электрондық зонаның формасын сипаттайды. энергия бірлігімен, ал – (энергия)² арқылы өлшенетіндіктен, келесідей жазуға болады:

, (21)

мұндағы А оң константа (тұрақты), ол күйлер тығыздығы функциясының таңдалған формасы мен электрондармен жартылай толтырылуына тәуелді.

(14) теңдіктегі функциясын алға шығу интегралдары квадраттарының жиынтығы ретінде, ал функциясын атомдарының зарядтарының тығыздықтарын қатты қою жолымен құрастырылатын электрондық зарядтардың локальді тығыздығы ретінде түсіндіруге болады. Мұндай түсіндірме (түсініктеме) болса, онда і түйіні мен осындай тығыздығы бар біртекті электрондық газдың ішіндегі атом ρтүйіндердің локальдік тығыздығының өлшемі ретінде түсіндіруге болады және бұл жағдайда (13) теңдеуді екі бөліктен тұратын қосынды ретінде қарастыруға болады: бірінші қосынды жұптық өзара әсермен байланысты, ал екіншісі локальді көлемнің функциясы болып табылады. ФС жазылу формасына қарай (13) теңдікте (8) теңдіктегі МПА потенциалдарына ұқсас. Бірақ олардың түсіндірмелері мүлде өзгеше. ФС потенциалдары жоғарыда көрсетілгендей күшті байланыс моделі негізінде алынған. Мұның себебі, МПА потенциалдарының F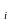 [ρ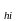 ] «бату» функционалдарына сәйкес келетін көпбөлшекті өзара әсерлесуге жауапты мүшелер квадраттық түбір түрінде көрсетілген. Сонымен қатар таза металдардан олардың қорытпаларына өту кезінде МПА потенциалдарына қарағанда ФС потенциалдары ыңғайсыздау. Осы қиындықтарға қарамастан ФС потенциалдары бірнеше жүйенің қорытпаларын сипаттау үшін жасалған, мысалы, асыл металдардың (Au, Ag) және мыстың қорытпалары.

3. Саттон мен Ченнің (СЧ) ұзақтан әсер етуші көпбөлшекті потенциалдары. СЧ-потенциалдар элементар металдардың он ГЦК-сының энергетикалық қасиеттерін сипаттайды. Типіне қарай бұл ФС-потенциалдар, сондықтан формасы бойынша МПА-потенциалдарға ұқсас. Олар көп атомы бар наножүйелерді компьютерлік есептеу кезінде қолдану үшін арнайы арналған.

(13) теңдікке сәйкес СЧ-потенциалдары арқылы берілген жалпы энергия келесі теңдікпен беріледі:

=ε[(1/2) φ (r )-c (ρ ) ], (22)

онда

φ (r )=(a/r ) (23)

және

ρ =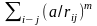 , (24)

ε – энергияның өлшемімен тең параметр; а – ұзындықтың өлшемімен, әдетте тепе-тең тор тұрақтысына тең ұзындықтың өлшеміне тең; m мен n – оң бүтін сандар, n>m. Потенциал мүшелерінің дәрежелік формасы алыс қашықтықтардағы өзара әсерлерді жақсырақ сипаттайтын ван-дер-вальстік «құйрықты» (хвост) беткейлік релаксация құбылыстарын сипаттауға жарамды, (22) теңдіктегі екінші N-бөлшекті мүше қамтамасыз ететін қысқа әсер ететін өзара әсерлерді біріктіре алатын жалғыз (бірыңғай) модельді жасау мақсатында қабылданған. ГЦК элементарлық ұяшығы бар дара металдар үшін (22) теңдіктегі потенциал толығымен m және n мәндерімен анықталады, себебі тордың тепе теңдік шартын с мәні тіркейді. Тордың 10 тұрақтысына тең үзіліс радиусы өлшемімен есептелген потенциал параметрлерінің мәні 3 кестеде көрсетілген.

3-кесте

Саттон-Чен потенциалдарының параметрлері

Элемент	m	n	ε(эВ)·10	с
Ni Cu Rh Pd Ag Ir Pt Au Pb Al	6 6 6 7 6 6 8 8 7 6	9 9 12 12 12 14 10 10 10 7	15,707 12,382 4,9371 4,1790 2,5415 2,4489 19,833 12,793 5,5765 33,147	39,432 39,432 144,41 108,27 144,41 334,94 34,408 34,408 45,778 16,399

Бұл параметрлер тор параметрлері мен когезия энергияларының тәжірибелік мәндерімен тура қиысуы негізінде алынған. m және n индекстері, олардың mn туындысы 12Ω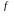 В/Е мәніне жақын бүтін сан болатындай етіліп бүтін сандармен шектеледі, онда Ω -ГЦК атомдық көлем, В - серпімділіктің есептік көлемдік модулі, Е -когезия энергиясының қиысу мәні.

СЧ-потенциалдары ГЦК- металдардың когезиондық энергияларын, серпімділіктің көлемдік модулдерін, серпімділік тұрақтыларын есептеуде және қатты қаптамасы бар гексагональдік, ГЦК-, ОЦК- жүйелердің салыстырмалы тұрақтылығын болжауда қолданылған. Алынған нәтижелер тәжірибелік нәтижелермен айтарлықтай үйлесімді (ұқсас). Бұл потенциалдар 13-309 атом өлшемі диапазонында металл кластерлердің жүйелік қасиеттерін өңдеуде қолданылған.