1.3. Вероятностные характеристики модуля комплексной случайной величины параметра режима

Одной из задач оценки интегральных характеристик режимов является определение модуля и аргумента полного тока в каждой ветви схемы замещения.

Введем обозначения:

С учетом этого математическое ожидание модуля комплексной случайной величины определится как

.

Второе слагаемое в этой формуле является поправкой на нелинейность функции. Оно зависит от математических ожиданий и дисперсий действительной и мнимой составляющих, а также корреляционного момента между ними.

Дисперсия модуля комплексной случайной величины равны

.

Максимальное значение модуля тока

.

В зависимости от требуемой степени надежности и конкретных условий верхняя граница отклонений выбирается при коэффициенте =23. Без учета поправок на нелинейность функции модуля тока формулы математического ожидания и дисперсии значительно упрощаются:

Тогда

.

Пример 2.

Рассчитать математические ожидания и дисперсии полных токов в ветвях электрической сети (рис.1.1). Исходные данные для расчета см. в примере 1.

Решение:

Для первой ветви сети математическое ожидание модуля полного тока с учетом поправок на нелинейность функции модуля равно

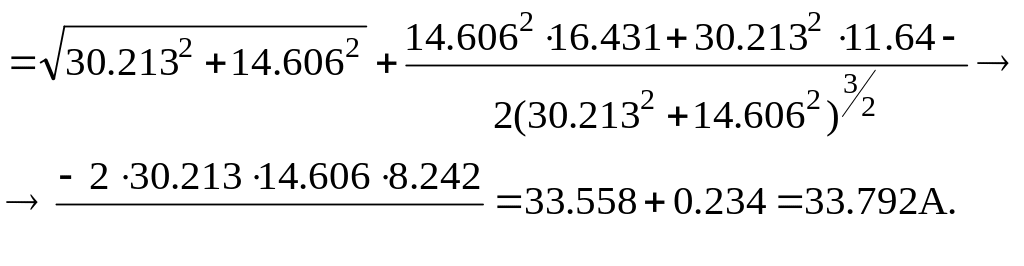
Дисперсия модуля полного тока нагрузки для первой ветви

Тогда максимальное значение модуля тока нагрузки при  = 2.5 для первой ветви можно найти из выражения

;

.

Результаты расчетов для остальных ветвей приведены в табл.1.2.

Таблица 1.2

Вероятностные характеристики полных токов в ветвях

№ ветви	1	2	3
	33.792	6.865	22.456
D(I),A	43.99	0.302	3.785
Imax,A	50.37	8.238	27.32

1.4. Вероятностные характеристики аргумента комплексной случайной величины параметра режима

Для полной характеристики комплексного значения тока нагрузки в любой ветви электрической сети в ряде случаев недостаточно знать модуль, необходимо хотя бы приближенно оценить аргумент. Если в качестве основной характеристики комплексной случайной величины (тока нагрузки) считать модуль, то числовые характеристики аргумента полного тока следует вычислять как условное математическое ожидание и дисперсию.

Тогда математическое ожидание случайной величины  (аргумента) относительно значения I составит

.

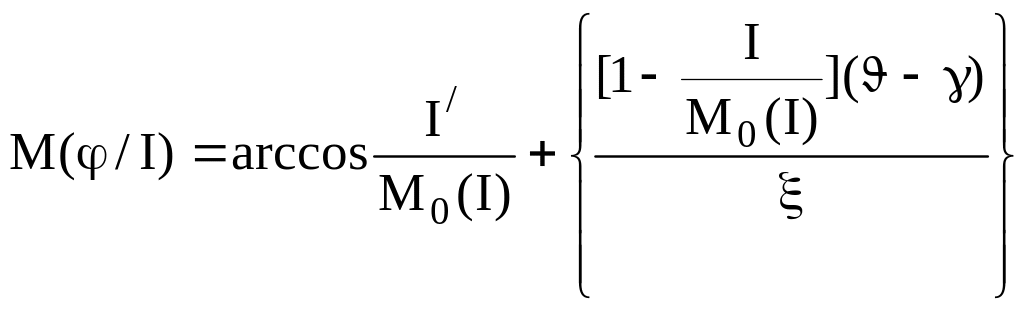Дисперсия аргумента:

где ;

;

Диапазон практически возможных значений аргумента при условии, что ток равен максимальному, определится из неравенства

Чем ближе значения расчетного тока и его математического ожидания, тем с большей точностью можно пользоваться приближенной формулой для определения математического ожидания аргумента

.

2. Расчет потерь мощности при вероятностном задании нагрузки

Полная мощность, теряемая в каждом элементе схемы сети, вычисляется по формуле

.

Вероятностные характеристики потерь мощности зависят от числовых характеристик квадрата полного тока.

Математическое ожидание квадрата тока, независимо от условий, определяется как:

.

Дисперсию квадрата полного тока в рамках корреляционной теории при произвольных функциях распределения можно вычислить с достаточной точностью лишь при условии относительно небольших вариаций действительной и мнимой составляющих:

С учетом выше изложенного, математическое ожидание потерь мощности

а максимальное значение

,

где D(S_i) – дисперсия потерь мощности, которая определяется по выражению

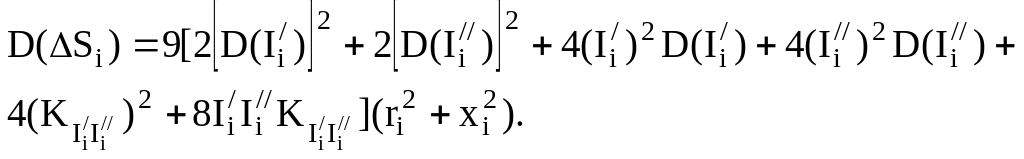Математическое ожидание суммарных потерь мощности во всех элементах сети

Ввиду второстепенного значения дисперсии потерь мощности для практических расчетов дисперсия суммарных потерь мощности приближенно определится без учета вероятностных связей:

.

Суммарные потери мощности являются функцией случайных коррелированных векторов нагрузки ветвей, которые характеризуются корреляционной матрицей.

Тогда максимально возможные потери мощности во всей сети

,

где =23 в зависимости от требуемой степени надежности получаемого результата.