31. Свойства алгоритмов
В настоящее время в различной научной литературе не однозначно трактуют свойства алгоритмов. Мы в данной дисциплине будем следовать рекомендациям Д. Кнута и выделим в качестве таковых следующие пять свойств:
- конечность;
- определенность;
- ввод;
- вывод;
- эффективность.
Рассмотрим существо этих свойств и подходы к их доказательству на примере алгоритма Евклида.
Конечность. При любом наборе входных данных алгоритм должен заканчиваться за конечное число шагов. Доказательством выполнения данного свойства является уменьшение исследуемой переменной на шаге i по сравнению с шагом i - l с учетом ее особенностей.
Так в алгоритме Евклида - это уменьшение переменной r (остаток от деления) на очередном шаге. В математике доказано, что убывающая последовательность положительных целых чисел имеет конечное число членов, поэтому алгоритм Евклида имеет конечное число шагов для любого изначально заданного n.
Процедура, обладающая всеми свойствами алгоритма, кроме конечности, называется методом вычисления. Так, Евклид предложил не только алгоритм вычисления НОД, но аналогичное ему геометрическое построение «наибольшей общей меры» длин двух отрезков, но это уже не алгоритм, а метод вычислений, т.к. выполнение его не заканчивается, если заданные длины оказываются несоизмеримыми.
Определенность. Каждый шаг алгоритма должен быть точно определен, т.е.. действия, выполняемые на каждом шаге должны быть определены математически строго и недвусмысленно для любого возможного случая.
В связи с этим для представления алгоритмов разработаны не только схемы алгоритмов, но и формально определенные языки программирования или машинные языки, в которых каждый оператор имеет строго определенное значение.
Метод вычисления, выраженный на языке программирования, будем называть программой.
Покажем доказательство этого свойства на примере алгоритма Евклида. Рассмотрим шаг деления n:m (n > m).
При выполнении этого действия исследователь должен точно понимать, что означает разделить n на m и что понимается под остатком r.
Вместе с тем, если не оговорено, что m и n оба положительные и целые числа, то это действие может трактоваться неоднозначно.
Например. Каким будет остаток
от деления числа (-8) на
,
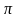или что понимать под остатком деления
59/13 на нуль.
В алгоритме Евклида имеется строгая оговорка о положительности и целостности чисел m и n и понятие остаток воспринимается исследователями однозначно.
Bвод. Алгоритм должен иметь некоторое (возможно равное нулю) число входных данных, т.е. . величин, которые задаются до начала его работы или определяются динамически во время его выполнения. Входные данные выбираются из некоторого строго определенного набора входных объектов. Например, в алгоритме Евклида имеется два входных значения m и n, обязательно принадлежащих множеству целых положительных чисел.
Вывод. У алгоритма должно быть одно или несколько выходных данных, т.е. величин, имеющих вполне определенную связь с входными данными.
У алгоритма Евклида имеется только одно выходное значение х = ni, вычисляемое на каждом шаге деления. Это НОД двух входных значений. То, что х = f(m,n) должно быть доказано.
Доказательство для алгоритма Евклида. После шага деления имеем
n = gm + r,
где g - некоторое целое число.
Если r = 0, то n - кратно m , и, очевидно, что n НОД m и n. Если же r ≠ О, то любой делитель обоих чисел m и n должен быть также делителем gm + r = n.
Таким образом, множество делителей чисел {m,n} cсовпадает с множеством делителей чисел {m,r}. Следовательно, пары чисел {m,n} и {m,r} имеют один и тот же НОД.
Массовость (общность, универсальность). Алгоритм должен быть разработан для решения задачи, поставленной в общем виде, так чтобы его можно было применить для решения всего класса подобных задач, различающихся исходными данными.
Отметим, что для практических целей ограничение, состоящее в конечности алгоритма не является жестким. Используемый на практике алгоритм должен иметь не просто конечное, а достаточно ограниченное (разумное)_ число шагов.
Например, известен алгоритм определения того, может ли игра в шахматы всегда быть выиграна белыми при условии, что не было сделано ни одной ошибки. Хотя сам этот алгоритм конечен, для его реализации требуется невероятно большой интервал времени. Это же характерно при работе с конечными, но очень большими числами, используемыми в криптографии.