11. Мера количества информации к. Шеннона для сообщений с неравновероятными независимыми символами.

Любая теория математически строга своими допущениями и ограничениями. Так, формула Хартли, с точки зрения теории вероятности, справедлива только в том случае, если символы в сообщении, формируемом дискретным источником, равновероятны и несовместны (это определил и сам Хартли), но также и независимы (это доказали К. Шеннон А.Я. Хинчин). В реальных СПИ такие ограничения чаще всего не выполняются.

Особенно это характерно для передачи текстовых сообщений на различных языках. Так в тексте, написанном на английском языке чаще всего встречается буква е, на русском языке – буква а, на украинском языке – буква о. В русском тексте вероятность появления буквы о принято считать равной 0,09, в то время как для буквы ф – 0.002. Для оценки количества информации в таких сообщениях применение меры Р. Хартли становится некорректным.

Это ограничение снял в своей теории Клод Шеннон. Покажем, как он решил задачу определения количества информации в сообщениях, в которых символы являются несовместными, независимыми и неравновероятными.

Рассмотрим множество Х случайных событий х₁, х₂,...х_N , наступающих с вероятностями:

р(х₁)= р₁, р(х₂)= р₂ , ..., р(х_N)=р_N

Назовем это законом распределения вероятностей. Пусть эти события независимы, несовместны и составляют полную группу событий, т.е. р₁ + р₂ + ...+ p_N = 1.

Множество, удовлетворяющее указанным требованиям, Шеннон назвал ансамблем случайных событий.

Неопределенность исхода опыта с ансамблем, который записывается законом распределения вида

Х = х₁, х₂, ... , х_m

p₁ p₂ p_m ( 11 )

, причем ,

К.Шеннон предложил находить по формуле

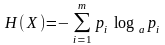( 12 )

Эта формула в теории информации носит название формулы Шеннона.

Пример 2. Пусть источник информации формирует сообщение Х, состоящее из 4 –х символов х₁,х₂,х₃,х_{4 ,} вырабатываемых с вероятностями р(х₁) = 1/2 , p(x₂) = 1/4, p(x₃) = p(x₄) = 1/8.

Требуется найти среднее количество информации, передаваемое с каждым символом

I(X) = H(X) = - (1/2 log ₂1/2 +1/4 log₂ 1/4+ 2 1/8 log₂ 1/8) =

• (- 1/2 -1/2 – 3/4) = 7/4 дв.ед/ симв. (бит/симв.)

В формуле (12) величину Н(Х) – Шеннон назвал энтропией ансамбля дискретных сообщений(в Н(Х) – Х – не аргумент функции, а обозначение ансамбля). Такие сообщения, которые в любой момент времени могут принимать только одно значения называют простыми.

Чем руководствовался Шеннон при выводе формулы (12)? Чтобы ответить на этот вопрос, рассмотрим ряд примеров.

Пример 1. Пусть имеем систему, которая может принимать два независимых несовместных состояния х₁ и х₂ с вероятностями соответственно р(x₁)=р(x₂)=0,5 и другую систему Y, которая также может принимать два состояния y₁ и y₂, но с вероятностями соответственно p(y₁)=0,1 и P(y₂)=0,9.

С точки зрения неопределенности состояния систем Х и Y можно качественно предположить, что у системы Х она больше, чем у системы Y, так как для системы Y наиболее вероятно, что она находится в состоянии y₂. Следовательно, можно отметить, что степень неопределенности, а также ее количественная мера – энтропия являются функциями вероятностных характеристик, того или иного состояния системы (исхода опыта).

По формуле Шеннона это можно доказать количественно. Например, при основании логарифма а = 2, получим

- для системы Х:

I(X) = H(X)_{до опыта} =

= -(

= ;

- для системы Y:

I(Y) = H(Y)_{до опыта} =

= -(

= .