10. Разрешающая способность микроскопа.

Соответствующим подбором линз можно обеспечить весьма большое увеличение оптического микроскопа (несколько тысяч раз), однако это нецелесообразно, так как все. равно возможность различения мелких деталей предмета нарушается дифракционными явлениями. Эти явления ограничивают полезное увеличение микроскопа.

При прохождении света через мельчайшие детали предмета происходит дифракция, в результате которой изображение этих деталей может терять резкость, может иметь место нарушение геометрического подобия изображения предмету и, наконец, изображение может вообще не получиться. Поэтому, например, в оптическом микроскопе невозможно видеть фильтрующиеся вирусы, отдельные белковые молекулы и т.п.

Свойство оптической системы давать раздельное изображение двух близко расположенных светящихся (или освещенных) точек называют разрешающей способностью системы и характеризуют наименьшим возможным расстоянием между этими точками. Это расстояние называют пределом разрешения оптического прибора. Чем меньше предел разрешения, тем выше разрешающая способность оптического прибора.

П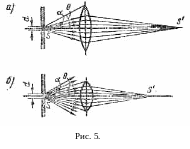 рименяя это понятие к условиям микроскопирования биологических объектов, можно считать, что предел разрешения обусловливает наименьшую величину тех структурных деталей», которые могут различаться в препарате.

Теория разрешающей способности микроскопа разрабатывалась Э. Аббе, а затем Л. И. Мандельштамом и Д. С. Рождественским. Разрешающая способность микроскопа в целом определяется разрешающей способностью объектива, в который непосредственно входят лучи света, днфрагировавшие на предмете. Основным элементом, обусловливающим разрешающую способность объектива, является его апертурный угол.

Рассмотрим образование с помощью объектива изображения светящегося отверстия S достаточно малого диаметра d, на которое падает пучок параллельных монохроматических лучей (рис. 5). Проходя через отверстие, свет испытывает дифракцию. Объектив собирает дифрагировавшие лучи и в сопряженной плоскости образует изображение S' отверстия. При этом возможны два случая. Во-первых, когда апертурный угол объектива больше угла дифракции лучей или равен ему ( ), тогда все дифрагировавшие лучи принимают участие в образовании изображения (рис. 5, а); в этом случае изображение будет геометрически подобно, предмету. Во-вторых, когда апертурный угол объектива, ограничивающий конус входящих в него лучей, меньше угла дифракции лучей ( ), тогда не все исходящие из отверстия лучи принимают участие в образовании изображения (рис. 5, б); в этом случае можно ожидать, что изображение не будет полностью геометрически подобно предмету. Степень нарушения подобия будет зависеть от того, какая часть дифрагировавших лучей не попадает в объектив и не принимает участия в образовании изображения.

Угол дифракции лучей тем больше, чем больше длина волны и чем меньше диаметр d отверстия, т. е. . Тогда в предельном случае, когда , между апертурным углом , длиной волны и диаметром отверстия d можно установить аналогичное соотношение , откуда . Таким образом, диаметр d отверстия, при котором сохраняется подобие изображения предмету, может быть тем меньше, чем короче длина волны и чем больше апертурный угол объектива.

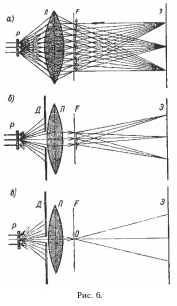
В теории Аббе в качестве микроскопируемого предмета рассматривается дифракционная решетка (рис. 6), которая освещается пучком перпендикулярно падающих на нее параллельных монохроматических, лучей. Лучи, претерпевшие дифракцию на щелях решетки Р, собираются объективом Л в его фокальной плоскости, образуя систему дифракционных максимумов (0, 1 и 1’, 2 и 2', 3 и 3’ и т. д.). За фокальной плоскостью лучи, образующие максимумы различных порядков, расходятся и, пересекаясь между собой в сопряженной плоскости, дают на экране изображение решетки. Если в его образовании принимают участие лучи от всех максимумов (рис. 6, а), то изображение будет резким и геометрически подобным предмету. Если с помощью диафрагмы Д уменьшать апертурный угол объектива (рис. 6, б), то лучи, образующие максимумы более высоких порядков, не попадут в линзу и не будут участвовать в образовании изображения. Изображение будет терять резкость и тем больше, чем меньше апертурный угол. Если апертурный угол уменьшить так, что в линзу попадут только лучи, образующие нулевой максимум (рис. 6, в), изображение решетки не получится, так как на экран будут падать лучи, не пересекающиеся между собой.

Как показал Аббе, для разрешения щелей в изображении дифракционной решетки необходимо, чтобы в образовании ее изображения участвовали лучи от максимумов нулевого и первого порядков хотя бы с одной стороны. Для этого направления лучей, образующих эти максимумы, должны быть в пределах апертурного угла объектива. Другими словами, апертурный угол объектива должен быть больше угла отклонения лучей, образующих максимум первого порядка, или в пределе равен ему: . Предел разрешения в этом случае может быть приравнен периоду решетки: . Тогда, используя формулу дифракционной решетки и подставляя в нее указанные величины, получим

,

т. е. предел разрешения численно равен отношению длины волны света к синусу апертурного угла объектива.

Если световой пучок падает на решетку под углом , равным апертурному углу , то, как показано на рис. 7, в этом случае апертурный угол может быть приравнен только половине угла дифракции, следовательно,условия разрешения улучшаются. В наших приближенных рассуждениях (см. рис. 5) это соответствует условию , т. е. при том же апертурном угле предел разрешения уменьшается в два раза. А в теории Аббе (см. рис. 7) формула принимает вид:

.

Дальнейшим усовершенствованием микроскопа явилось применение иммерсионного объектива. Так называют объектив, у которого пространство между предметом (покровным стеклом препарата) и входной линзой заполняется жидкостью с показателем преломления, близким к стеклу, например глицерином или. При иммерсионном объективе, во-первых, значительно увеличивается яркость изображения и, во-вторых, повышается разрешающая способность микроскопа.

В иммерсионном объективе, где между предметом и объективом находится среда с показателем преломления п, длина волны света, проходящего в объектив, , где – длина волны света в воздухе. Подставляя эти данные в формулу для предела разрешения, получим

,

т. е. предел разрешения иммерсионного объектива при наклонном освещении предмета численно равен отношению длины волны света к удвоенному произведению показателя преломления иммерсионной среды на синус апертурного угла объектива.

Величина для сухого или для иммерсионного объектива называется численной апертурой. Поэтому можно сказать, что предел разрешения микроскопа равняется длине волны света, при котором производится наблюдение, деленной на численную| апертуру при перпендикулярном падении света на предмет: или деленной на удвоенную численную апертуру при наклонном освещении: ; при иммерсионном объективе .

Численная апертура объектива, характеризуя предел разрешения, позволяет сравнивать между собой разрешающую способность различных микроскопов. Последняя тем выше, чем больше апертура.

Таким образом, в оптическом микроскопе разрешаются объекты (или детали их структуры) размером не менее 0,2 – 0,3 мкм. Для того чтобы эти объективы были различимы также и глазом, увеличение К микроскопа должно быть не меньше величины, определяемой соотношением пределов разрешения глаза и микроскопа :

.

Такое увеличение называют; полезным увеличением микроскопа.