Министерство образования Республики Беларусь Белорусский государственный университет Механико-математический факультет

Кафедра теоретической и прикладной механики

КУРСОВАЯ РАБОТА

Тема:

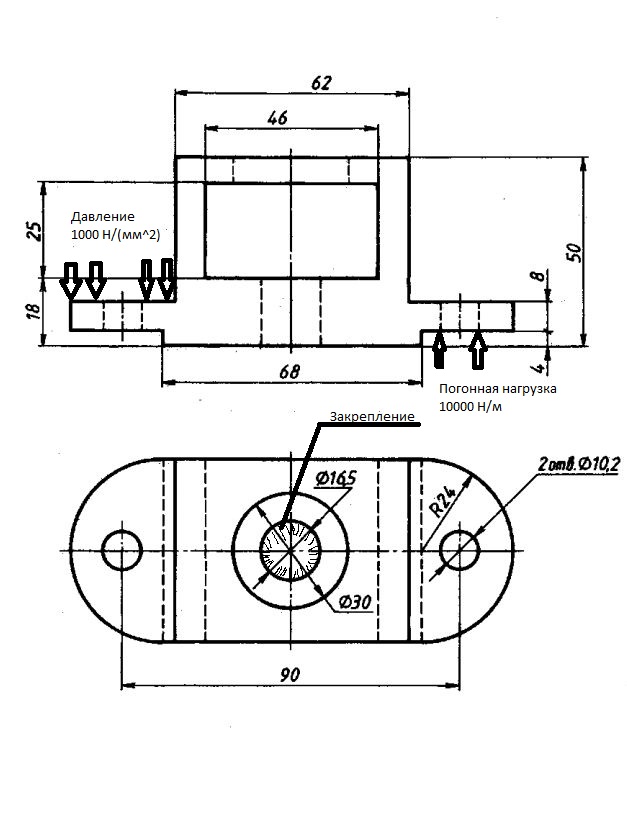
«Исследование напряжённо-деформированного состояния теплообменника в МКЭ пакетах»

Выполнил студент

III курса, 8 группы,

Филончик Евгений Сергеевич

Руководитель:

Громыко Олег Владимирович

Минск

2013

Оглавление

ВВЕДЕНИЕ…………………………………………………………………………. 3

ГЛАВА 1 ANSYS………………………………………………………………..…. 6

1.1 Построение детали…………………………….……………………………… 6

1.2 Анализ детали…………………………..…….…………………………...…... 23

ГЛАВА 2 AutoCAD……………………………………………………………..…35

2.1 Построение детали ……………………………………………………………35

2.2 Анализ детали …….……………………………………………………...…... 41

ГЛАВА 3 Femap…….…………………………………………………………..…. 51

1.1 Построение детали…………………………….……………………………… 51

1.2 Анализ детали…………………………..…….…………………………...…... 63

ГЛАВА 4 ProEngineer…………………………………………………………..…. 75

1.1 Построение детали…………………………….……………………………… 75

1.2 Анализ детали…………………………..…….…………………………...…... 85

ГЛАВА 5 SolidWorks…………………………………………………………..…. 93

1.1 Построение детали…………………………….……………………………… 93

1.2 Анализ детали…………………………..…….…………………………...…..100

ГЛАВА 6 ANSYS Workbench…………………………………………………..109

1.1 Построение детали…………………………….……………………………109

1.2 Анализ детали…………………………..…….…………………………...…..118

ЗАКЛЮЧЕНИЕ…………………………………………………………….….…..126

БИБЛИОГРАФИЧЕСКИЙ СПИСОК…………………………………………..127

ПРИЛОЖЕНИЕ…….……………………...………………………………..……128

Введение

В настоящее время наиболее распространенным методом расчета сложных конструкций является метод конечных элементов (МКЭ). При его использовании конструкция, представляющая собой непрерывную среду, заменяется ее моделью, составленной из конечного числа блоков – элементов, поведение каждого из которых может быть определено заранее. Взаимодействие элементов между собой позволяет описать общую картину деформирования системы.

Например, оболочка, состоящая из гладкой панели и кольцевых и продольных подкреплений, может быть составлена из набора простых элементов: цилиндрической прямоугольной панели 1, прямого стержня 2, криволинейного стержня 3. Жесткости каждого из этих элементов должны быть определены заранее. На рисунке обозначены узловые точки А, В, С, D, по которым элементы собираются в общую систему. Напряженное состояние такой сложной конструкции может быть определено с помощью МКЭ с единых позиций.

С помощью МКЭ решено большое количество задач прочности, устойчивости и динамики конструкций. Он используется также для анализа нелинейных явлений, с его помощью удается решить сложные многомерные задачи оптимизации и т. п.

Основные достоинства МКЭ заключаются в его универсальности: возможности использовать элементы различных типов, произвольной геометрии рассматриваемой области, простоте приемов построения элементов высокой точности. В варианте метода, рассматриваемом ниже – методе перемещений, – при стыковке элементов требование удовлетворения естественных краевых условий необязательно.

Этот наиболее известный вариант МКЭ использует формулировку принципа возможных перемещений.

В матричной форме для трехмерного тела принцип возможных перемещений можно записать следующим образом:

Перепишем это же соотношение иначе:

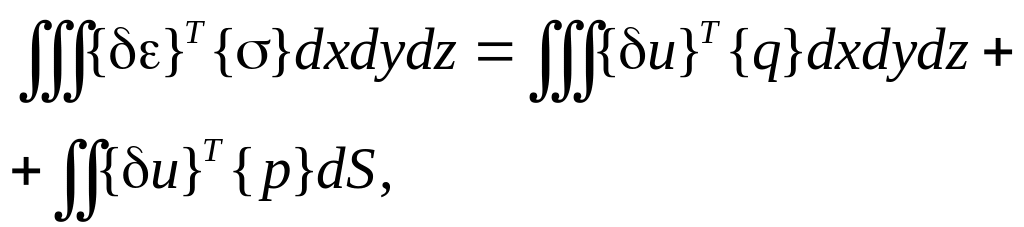(1.1)

где векторы напряжений и деформаций соответственно равны:

(1.2)

а векторы объемных, поверхностных сил и перемещений следующие:

(1.3)

Соотношение (1.1) не зависит от свойств материала и справедливо как для линейной, так и для нелинейной системы. Если линейно-упругое тело имеет начальные деформации (например, температурные), то физические соотношения принимают вид

(1.4)

где [D] – матрица упругих констант.

Подставляя соотношения (1.4) в уравнение (1.1), получаем

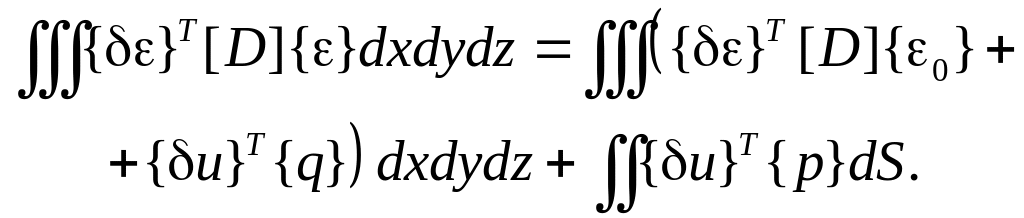(1.5)

Выражение (1.5) справедливо как для отдельного элемента, так и для всей системы в целом. Будем полагать, что оно относится к каждому элементу и интегрирование ведется по объему и поверхности элемента. Формулировка принципа возможных перемещений для системы элементов в целом выглядит так:

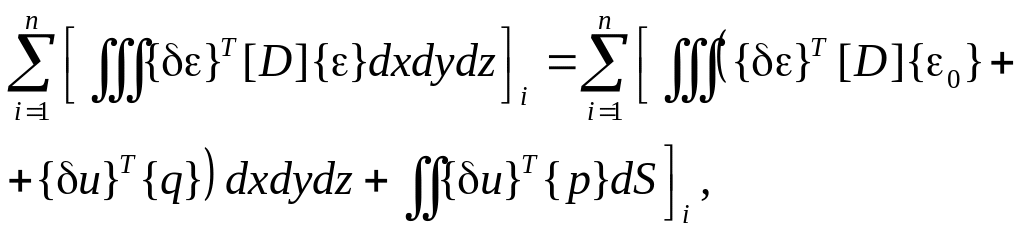(1.6)

где n – число элементов, на которое разбито исследуемое тело.

МКЭ использует процедуры различных вариационных методов. В рассматриваемом варианте метода так же, как и в методе Рэлея – Ритца, необходимо задаться функцией перемещений, но не на всей области, а лишь в пределах элемента.

Функции перемещений задают в виде полиномов по степеням пространственных координат х, у, z:

(1.7)

где [A] – матрица, зависящая от координат элемента; – вектор коэффициентов полиномиального разложения функций перемещений. Количество этих коэффициентов соответствует числу степеней свободы элемента, а сами коэффициенты связаны с узловыми перемещениями. Если обозначить вектор узловых перемещений элемента через , то функцию перемещений можно описать выражением

(1.8)

Воспользуемся соотношениями между деформациями и перемещениями (1.15). Подставляя в них зависимость (1.8), получим

(1.9)

В дальнейших расчетах важное значение имеет матрица , которая устанавливает связь деформаций с узловыми перемещениями. Вектор напряжений определяют по физическим соотношениям (1.4), которые с учетом связи (1.9) принимают следующий вид:

(1.10)

Правую и левую части условия равновесия (1.5) рассмотрим по отдельности. Подставляя вектор деформаций (1.9) в левую часть уравнения (1.5), выразим его через узловые перемещения и интеграл, который обозначим символом :

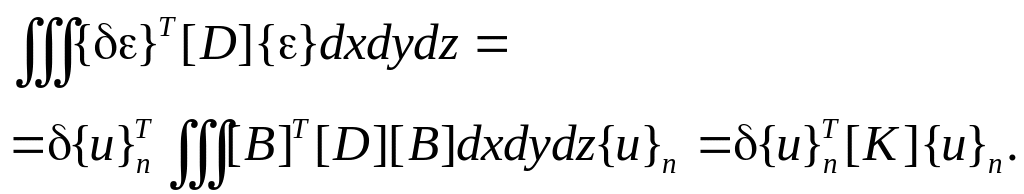(1.11)

В этом соотношении является матрицей, которая содержит информацию о поведении элементарного участка деформируемой системы. Это матрица жесткости элемента, являющаяся основной характеристикой системы в МКЭ.

Интегралы по объему и по поверхности в правой части выражения (1.5) представим следующим образом:

(1.12)

Так вычисляется вектор внешних сил , приведенных к узлам.

Если известны матрица , которая связывает перемещения в любой точке элемента с узловыми перемещениями (1.8), и матрица , входящая в соотношения между деформациями и перемещениями узлов элемента (1.9), то матрицу жесткости и вектор внешних узловых сил определяют по формулам:

(1.13)

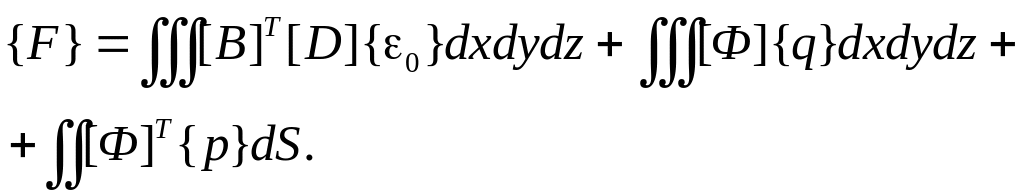(1.14)

Таким образом, условие равновесия каждого элемента имеет вид

(1.15)

Соотношения для всей системы приводятся к аналогичной форме, но вместо вектора узловых перемещений и матрицы жесткости элемента следует подставить вектор узловых перемещений всей системы (глобальный вектор перемещений) и соответствующую матрицу (общая или глобальная матрица жесткости):

(1.15')

При расчете конструкций с помощью МКЭ уравнение (1.15') является основным, позволяющим определить перемещения (и, воспользовавшись соотношением (1.10)), напряженное состояние в каждом элементе системы. Основная задача расчета конструкций методом конечных элементов заключается в определении матриц жесткости элементов, общей матрицы жесткости и вектора узловых сил .