7. Корреляционно-регрессионный анализ связи опф и прибыли предприятий отрасли

Установление наличия и характера связи.

Связь между факторными и результативными показателями может быть одной из двух видов: функциональной или корреляционной.

Функциональной, называется такая взаимосвязь, которая проявляется с одинаковой силой у всех единиц совокупности, независимо от изменения других признаков данного явления. Функциональные связи обычно выражаются формулами.

Корреляционной называется взаимосвязь между факторным и результа­тив­ным показателем, которая проявляется только «в общем и среднем» при массовом наблюдении фактических данных.

Содержательный анализ исходных данных выполнен ранее и установлено, что ОПФ – факторный признак , прибыль – результативный , поэтому на основании проведенных ранее вычислений можно сделать однозначный вывод, что связь между факторным и результативным признаком не полная, а проявляется лишь в общем, среднем, т.е. речь может идти только о корреляционном виде связи.

Непременными условиями корректного использования корреляционного метода являются достаточно большое число единиц совокупности, однородность совокупности и отсутствие выделяющихся, «аномальных» наблюдений, проверка которых уже выполнена ранее.

Для установки факта наличия связи, заполним групповую таблицу 9, по данным табл. 6; на рис. 1 построим поле корреляции, по исходным данным табл.2, и эмпирическую линию регрессии, по данным табл.9, принимая середину интервала за , за – прибыль в среднем на один предприятие:

Таблица 9
№ п/п	ОПФ, млн. руб.	Число предприятий	Середина интервала, млн. руб.	Прибыль в среднем на один предприятие, млн. руб.
I	770 – 825	10	797,5	15,48
II	825 – 880	3	852,5	19,23
III	880 – 935	7	907,5	19,54
IV	935 – 990	4	962,5	24,27
V	990 – 1045	2	1017,5	22,30

Анализ таблицы 9 свидетельствует, что существует прямая зависимость между величиной ОПФ и прибылью предприятий.

Теоретическая линия регрессии

Эмпирическая линия

регрессии

Рис.1. Корреляционное поле и линии регрессии

Поле корреляции, имеет форму вытянутого эллипса и ясно показывает, что имеется тенденция к росту из левого нижнего угла в правый верхний. Значит, имеется прямая корреляционная зависимость между ОПФ и прибылью предприятий.

Эмпирическая линия регрессии также имеет некоторую тенденцию к росту, что также свидетельствует о наличии прямой корреляционной зависимости между ОПФ и прибылью предприятий.

Определение тесноты и существенности связи.

Эмпирическая линия регрессии (рис. 1) – ломаная линия. Изломы этой линии свидетельствуют о влиянии на признак « » прочих факторов, помимо признака « ». Чтобы абстрагироваться от влияния прочих факторов, нужно прибегнуть к выравниванию полученной ломаной линии регрессии. Для этого сначала необходимо установить теоретическую форму связи, т.е. выбрать определенный вид функции, наилучшим образом отображающий характер изучаемой связи.

Выбор формы связи имеет решающее значение в корреляционно-регрессионном анализе, но этот выбор всегда связан с некоторой условностью, вызванный тем, что нужно находить форму функциональной зависимости, в то время как зависимость лишь в той или иной степени приближается к функциональной. Но если зависимость довольно высокая, т.е. довольно близко приближается к функциональной, тогда именно теоретическая линия регрессии и ее параметры приобретают практическое значение.

На основании качественного анализа исходных данных (табл.2) и эмпирической линии регрессии (рис.1) можно предположить, что между ОПФ и прибылью предприятий существует линейная зависимость. Для определения тесноты этой зависимости воспользуемся линейным коэффициентом корреляции:

,

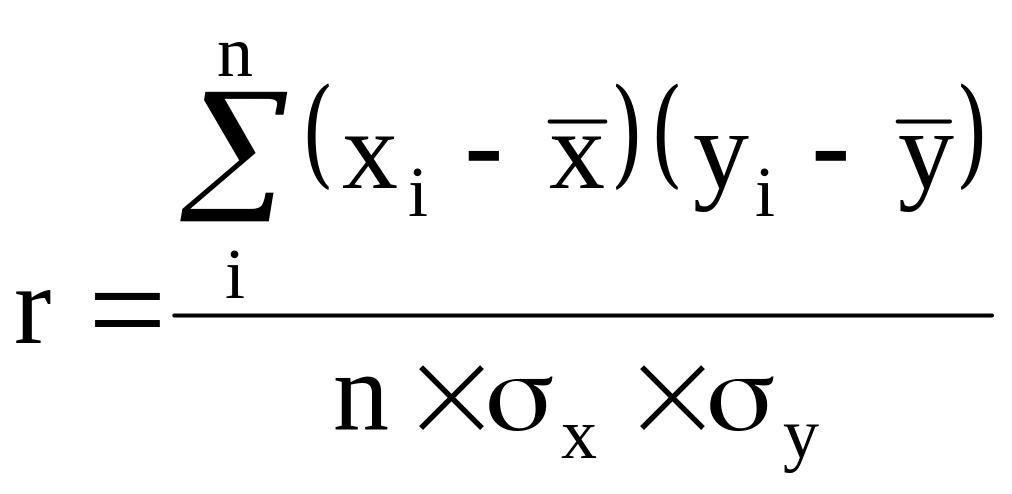где		значение факторного показателя;
		среднее значение факторного показателя;
		значение результативного показателя;
		среднее значение результативного показателя;
		число единиц в совокупности;
		среднее квадратическое отклонение по факторному показателю;
		среднее квадратическое отклонение по результативному показателю;

Для вычисления линейного коэффициента корреляции воспользуемся расчетами, выполненными в табл. 3, тогда

Среднее значение и среднее квадратическое отклонение результативного показателя рассчитывается аналогично факторному:

; ,

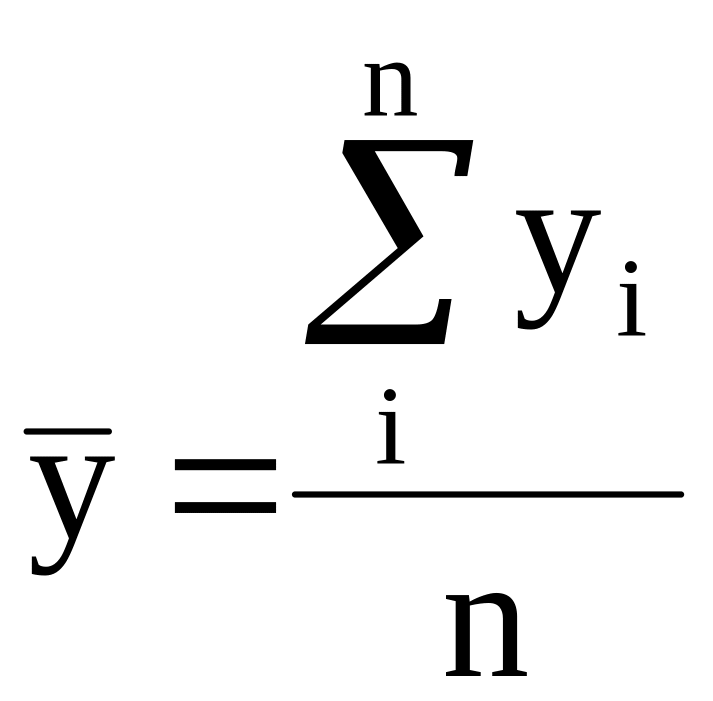где		среднее значение результативного показателя;
		среднее квадратическое отклонение по результативному показателю;
		значение результативного показателя;
		число единиц в совокупности;

.

Коэффициент корреляции показывает не только тесноту, но и направление связи. Его значение изменяется от до . Если коэффициент имеет знак минус, значит, связь обратная, если имеет знак плюс, то связь прямая. Близость к единице в том и в другом случае характеризует близость к функциональной зависимости.

Таким образом, значение свидетельствует о прямой и достаточно тесной связи между величиной ОПФ и прибылью предприятия.

Однако, чтобы это утверждать, необходимо дать оценку существенности линейного коэффициента корреляции, что можно выполнить на основании расчета t-критерия Стьюдента:

,

где		линейный коэффициент корреляции;
		число единиц в совокупности.

.

Для числа степеней свободы и уровня значимости 1% табличное значение , т.е. . Следовательно, с вероятностью можно утверждать, что в генеральной совокупности существует достаточно тесная прямая линейная зависимость между величиной ОПФ и прибылью предприятия.

Построение уравнения парной регрессии ОПФ и прибыли

Для выравнивания эмпирической линии регрессии (рис.1) необходимо найти теоретическое уравнение связи. На основании вычислений тесноты линейной взаимосвязи, выравнивание можно производить по прямой, т.е. теоретическое уравнение связи, имеющее линейный характер, в общем виде будет иметь вид:

,

Найти теоретическое уравнение связи – значит, в данном случае, определить параметры прямой. Это можно сделать способом наименьших квадратов, который дает систему нормальных уравнений для нахождения параметров прямой:

,

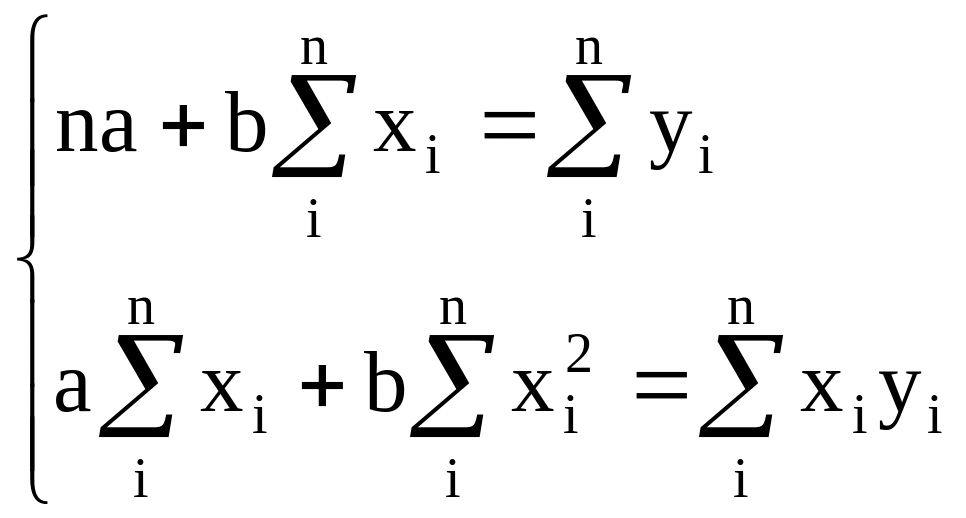
где		значение факторного показателя;
		значение результативного показателя;
		число единиц в совокупности.

Тогда:

;

.

где		коэффициент корреляции;
		среднее квадратическое отклонение по факторному показателю;
		среднее квадратическое отклонение по результативному показателю;
		среднее значение результативного показателя;
		среднее значение факторного показателя.

.

.

Следовательно, теоретическое уравнение связи имеет вид (см. рис.1):

.

С экономической точки зрения коэффициент регрессии говорит о том, что при увеличении ОПФ на прибыль возрастает на или на

По коэффициенту регрессии можно вычислить коэффициент эластичности.

Коэффициент эластичности показывает, на сколько процентов увеличится результативный показатель при увеличении факторного признака на 1%:

,

где		среднее значение результативного показателя;
		среднее значение факторного показателя;

.

Следовательно, при увеличении ОПФ на 1%, прибыль увеличивается на 1,82%.