6. Анализ динамики и прогнозирование прибыли

Анализ динамики выполняется путем расчета:

1. показателей, характеризующих изменение анализируемого показателя по периодам;

2. средних показателей динамики.

Показатели, характеризующие изменение анализируемого показателя по периодам, могут быть рассчитаны цепным и базисным методом. Цепные показатели динамики характеризуют изменение каждого последующего показателя по сравнению с предыдущим, а базисные по сравнению с уровнем, принятым за базу сравнения. К таким показателям относятся:

• Абсолютный прирост:

;

,

где		уровень сравниваемого периода;
		уровень предыдущего периода;
		уровень базисного периода.

• Темп роста:

;

,

где		уровень сравниваемого периода;
		уровень предыдущего периода;
		уровень базисного периода.

• Темп прироста:

;

,

где		цепной темп роста сравниваемого периода;
		базисный темп роста сравниваемого периода.

• Абсолютное значение одного процента прироста:

,

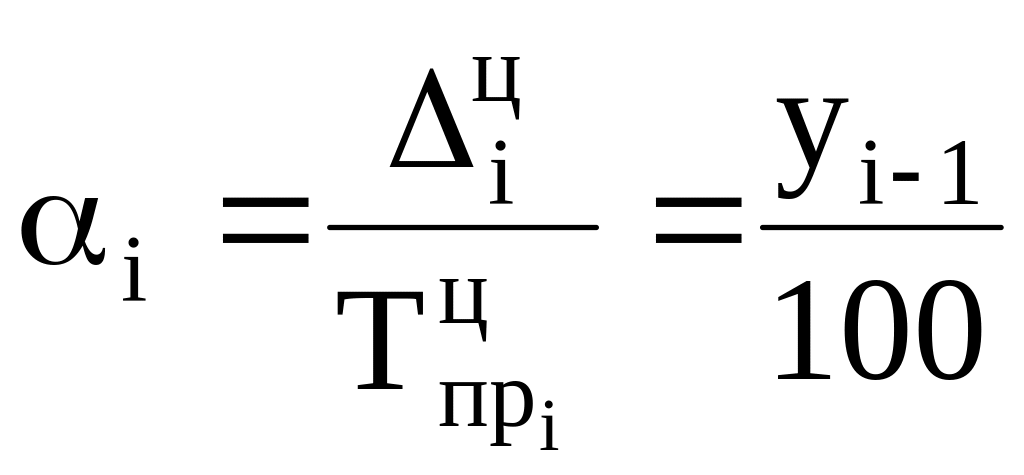где		цепной абсолютный прирост сравниваемого периода;
		цепной темп прироста сравниваемого периода;
		уровень предыдущего периода.

• Пункты роста:

,

где		базисный темп роста сравниваемого периода;
		базисный темп роста предыдущего периода;

К средним показателям динамики относятся:

• Средний уровень ряда:

,

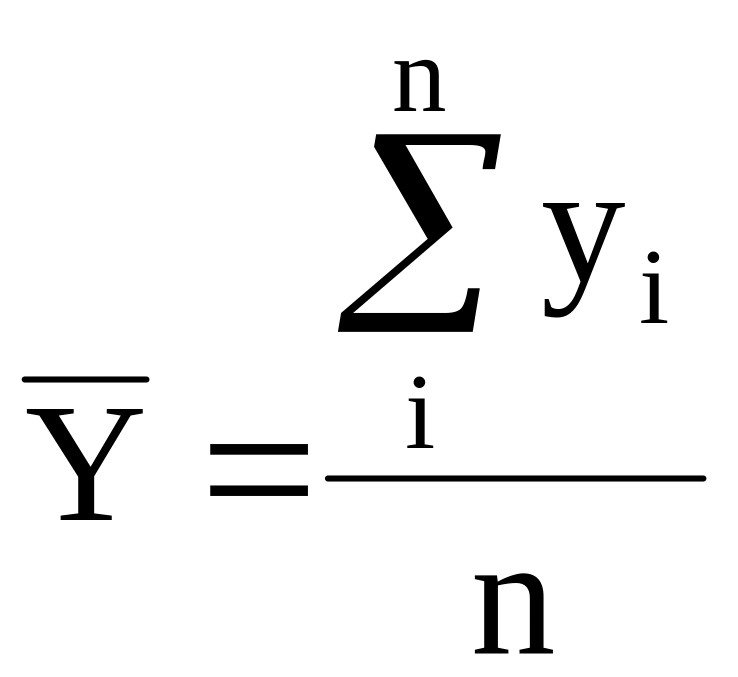где		уровень периода;
		число уровней ряда динамики в изучаемом периоде.

• Средний абсолютный прирост:

,

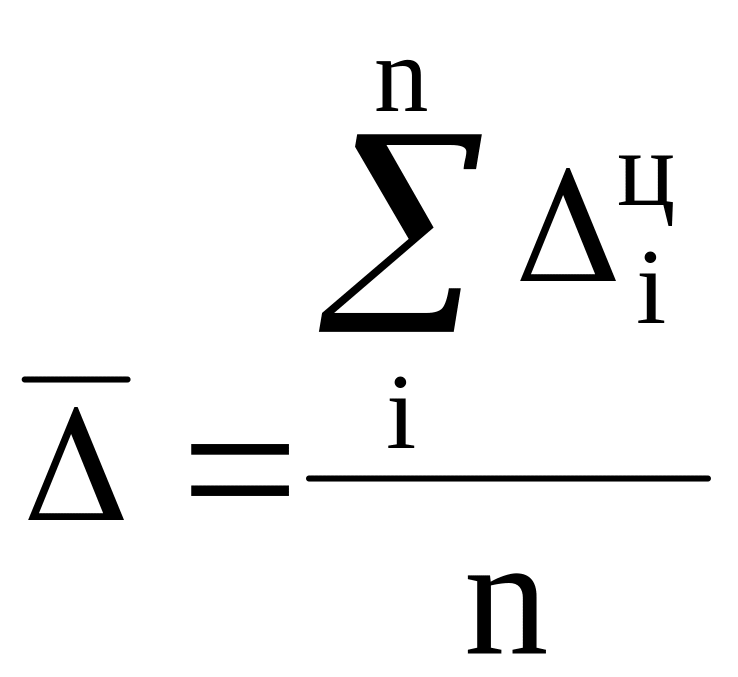где		цепной абсолютный прирост периода;
		число годовых абсолютных приростов.

• Средний коэффициент роста:

,

где		последний уровень ряда динамики в изучаемом периоде;
		уровень базисного периода;
		число уровней ряда динамики в изучаемом периоде.

• Средний темп роста:

,

где

средний коэффициент роста;

• Средний темп прироста:

,

где

средний коэффициент роста.

Для выполнения анализа динамики, из табл.2 по данным о прибыли предприятия №1 за отчетный год (4 квартала), рассчитаем все приведенные выше показатели динамики, при этом за уровень базисного периода примем показатель прибыли за IV квартал предыдущего года. Результаты вычислений показателей, характери­зующих изменение прибыли предприятия по периодам отражены в табл. 7:

Таблица 7
Период времени	Прибыль млн. руб.	Абсолютный прирост, млн. руб.		Темп роста, %		Темп прироста, %		Абсолютное значение 1% прироста	Пункты роста, %
		Цеп­ной	Базис­ный	Цеп­ной	Базис­ный	Цеп­ной	Базис­ный
IV кв. пре­дыду­щего года	25,4	—	—	—	—	—	—	—	—
I кв.	28,4	3,0	3,0	111,8	111,8	11,8	11,8	0,254	—
II кв.	27,6	- 0,8	2,2	97,2	108,7	- 2,8	8,7	0,284	- 3,1
III кв.	34,3	6,7	8,9	124,3	135,0	24,3	35,0	0,276	26,3
IV кв.	35,1	0,8	9,7	102,3	138,2	2,3	38,2	0,343	3,2

Т.к. изучаемым периодом является отчетный год, то средний уровень ряда:

Средний абсолютный прирост за отчетный год:

Средний темп роста прибыли за отчетный год:

Средний темп прироста прибыли за отчетный год:

Таким образом, средняя квартальная величина прибыли предприятия за отчетный год составила , а ее среднеквартальный абсолютный прирост составил , что соответствует среднеквартальному темпу роста , и среднеквартальному темпу прироста .

Показатели динамики свидетельствуют о ежеквартальном росте прибыли, кроме II квартала отчетного года, когда было допущено снижение на , что составило . В целом за отчетный год прибыль предприятия возросла на  , что составило .

Прогнозирование значения прибыли

Найти прогнозное значение прибыли на следующий период, т.е. I квартал следующего года, можно использовать метод аналитического выравнивания по прямой. Для этого необходимо найти уравнение тренда, вида:

,

где

порядковый номер периодов времени

Чтобы найти уравнение тренда, нужно определить параметры и . Это можно сделать способом наименьших квадратов, который дает систему нормальных уравнений прямой:

,

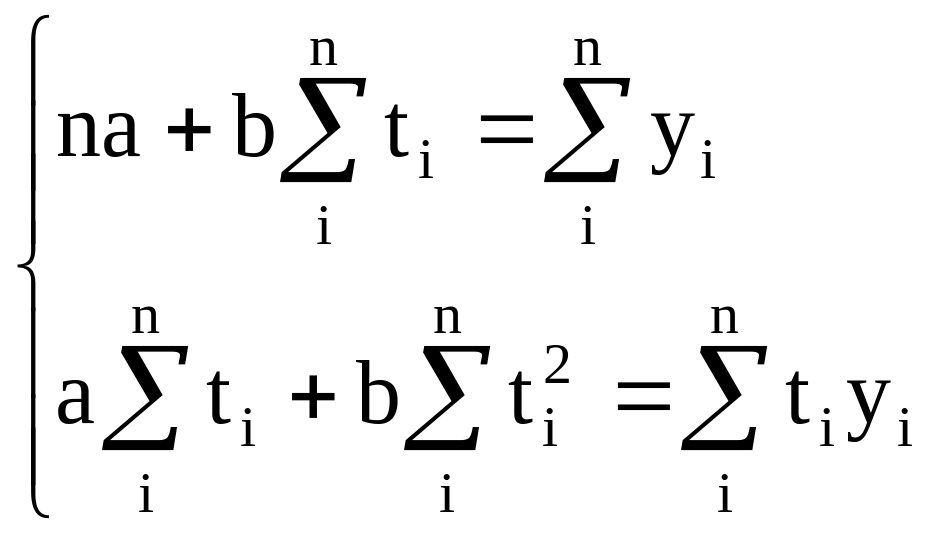
где		значение прибыли предприятия за период;
		номер периода;
		число периодов.

Нахождение параметров упрощается при использовании метода отсчета от условного нуля, тогда и система уравнений принимает вид:

.

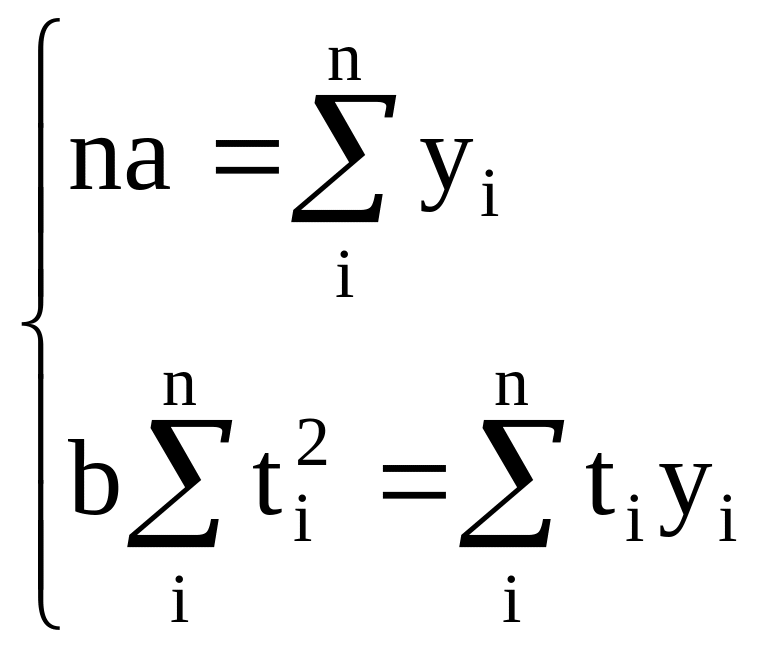
Тогда:

;

.

Для нахождения прогнозного значения прибыли предприятия №1 из табл.2, рассчитаем параметры уравнения тренда по результатам вычислений, произведенных в табл.8:

;

.

Тогда, уравнение тренда, для расчета теоретического значения прибыли, имеет вид:

.

Таблица 8
Период времени	Прибыль, млн. руб.	Условное обозначение периодов,			Теоретические (расчетные) значения прибыли, млн. руб.
1	2	3	4	5	6	7	8
IV кв. пре­дыду­щего года	25,4	-2	- 50,8	4	25,10	0,30	0,0900
I кв.	28,4	-1	- 28,4	1	27,63	0,77	0,5929
II кв.	27,6	0	0,0	0	30,16	- 2,56	6,5536
III кв.	34,3	1	34,3	1	32,69	1,61	2,5921
IV кв.	35,1	2	70,2	4	35,22	- 0,12	0,0144
Итого	150,8		25,3	10	150,80		9,8430

Для нахождения прогнозного значения прибыли на I квартал следующего года, необходимо в уравнение тренда подставить соответствующее значение :

Этот прогноз называется точечным, и фактическое значение всегда будет сколько-нибудь отличаться от этой величины, поэтому необходимо найти доверительные интервалы прогноза:

,

где		значение точечного прогноза;
		табличное значение -критерия Стьюдента при уровне значимости ;
		среднее квадратическое отклонение от тренда;
		число уровней ряда.

Среднее квадратическое отклонение от тренда рассчитывается по формуле:

,

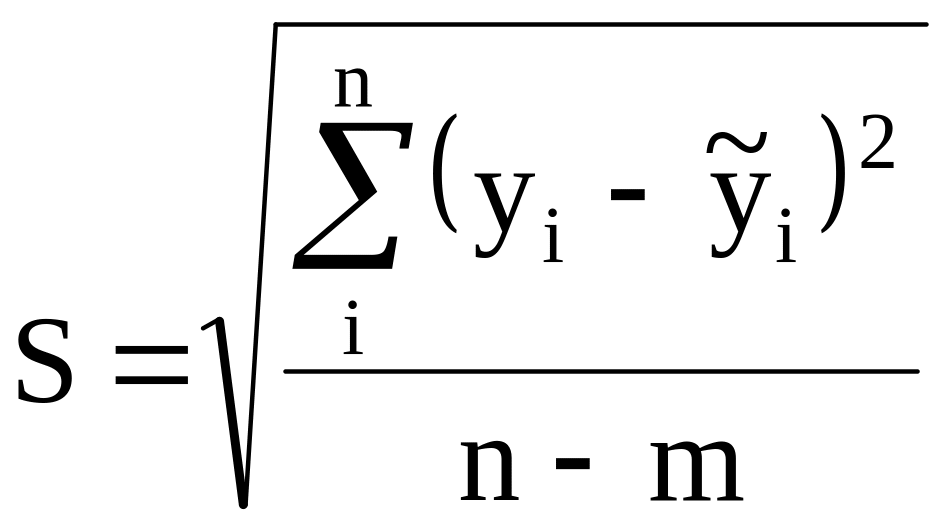где		фактическое значение уровня динамического ряда;
		расчетное значение уровня динамического ряда;
		число уровней ряда;
		число параметров в уравнении тренда (для прямой ).

.

Определить относительную ошибку уравнения можно как коэффициент вариации по формуле:

,

где		среднее квадратическое отклонение от тренда;
		среднее значение динамического ряда;

.

Следовательно, ошибка невелика и составляет .

По таблице Стьюдента, при уровне значимости 5% и числе степеней свободы , значение . Тогда доверительный интервал:

;

;

.

С вероятностью 0,95 можно утверждать, что прибыль предприятия №1 в I квартале следующего года будет находиться в пределах от 35 млн.173 тыс. руб. до 40 млн. 327 тыс. руб.

Характеристики качества статистической модели прогноза прибыли и ее надежности для выполнения прогнозных расчетов определяется с использованием критерия:

- хорошее качество модели;

- удовлетворительное качество модели;

- неудовлетворительное качество (прогнозная модель практически не улучшает простейший прогноз «по среднему»),

где:

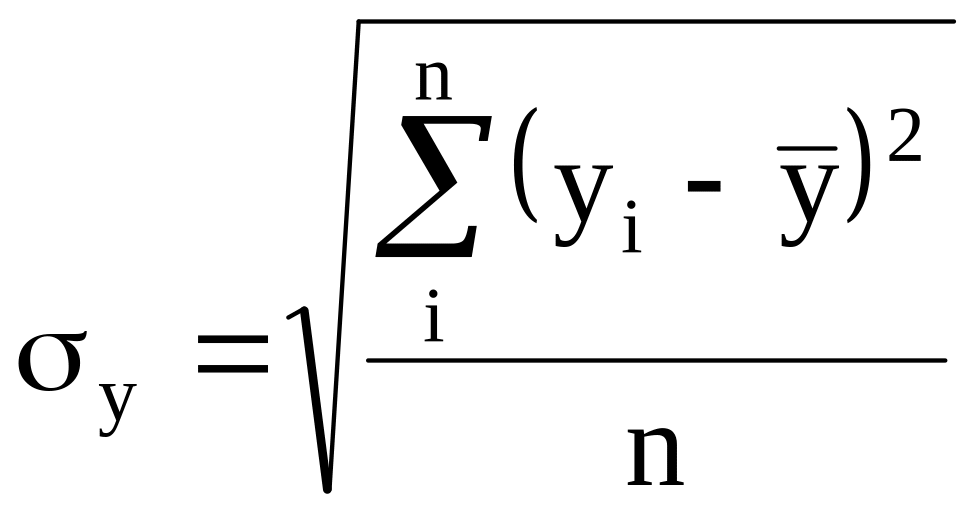- среднеквадратическое отклонение величины прибыли.

Данную величину определим на основе данных табл.3

Допустимая ошибка прогноза при использовании модели для прогноза рассчитывается по формуле:

Согласно этих данных значение критерия

Следовательно, данную прогнозную модель можно охарактеризовать как близкую к хорошей.

Значение допустимой ошибки прогноза: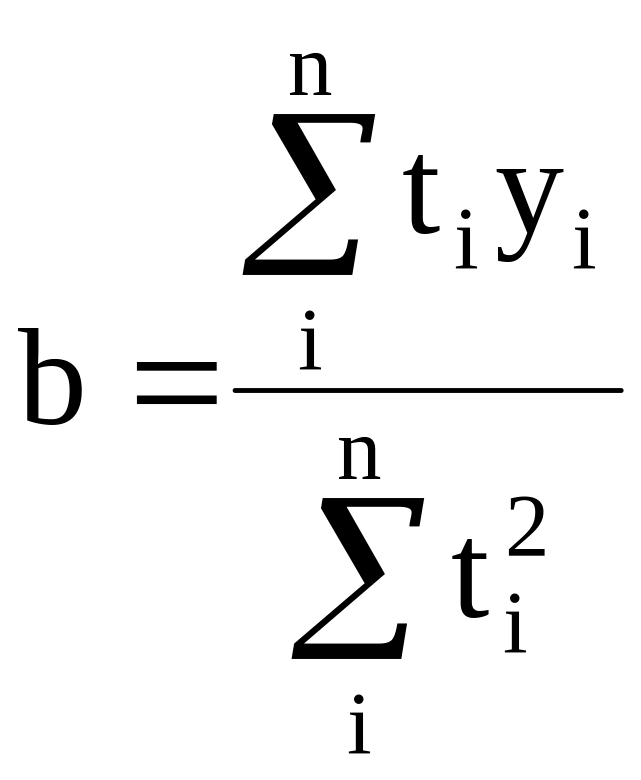