5. Определение характеристик генеральной совокупности

По условию задания предполагается, что исходные данные по 26 предприятиям являются 5% выборкой из некоторой генеральной совокупности. Для определения характеристик генеральной совокупности необходимо:

• определить характеристики выборочной совокупности: среднюю величину; дисперсию; долю единиц, обладающих значением изучаемого признака; дисперсию доли;

• рассчитать ошибки выборки;

• распространить результаты выборки на генеральную совокупность путем определения доверительных интервалов, в которых с определенной вероятностью можно гарантировать нахождение характеристик генеральной совокупности.

Для определения характеристик выборочной совокупности, воспользуемся результатами предыдущих расчетов, в результате которых определили, что:

средняя величина ОПФ составляет: ;

дисперсия равна:

Доля предприятий, у которых ОПФ превышает среднюю величину, для выборочной совокупности определяется по первичным данным табл. 2. Число таких предприятий равно 13, тогда их доля в выборочной совокупности составляет:

.

Дисперсия доли рассчитывается, как произведение значения доли на дополнение ее до единицы, т.е.: . Тогда, дисперсия доли составляет:

Для расчета ошибок выборки можно воспользоваться формулами для бесповторного отбора, т.к. из условия задания можно определить численность генеральной совокупности. Тогда, средняя ошибка выборки для средней величины:

,

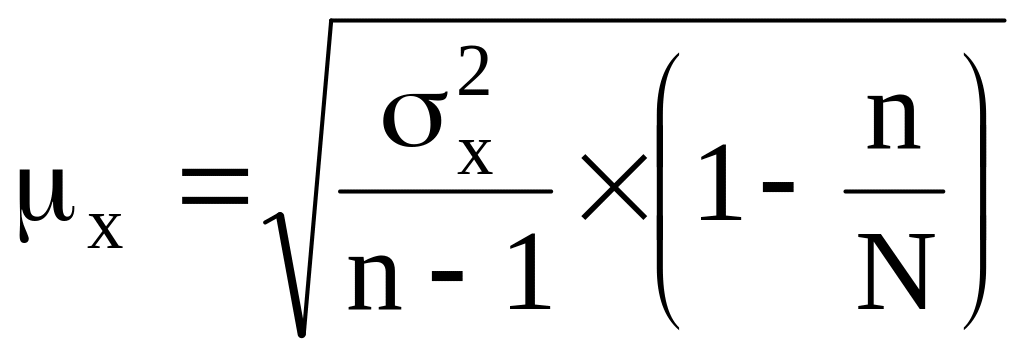где		дисперсия выборочной совокупности;
		численность единиц выборочной совокупности;
		численность единиц генеральной совокупности;

Т.к. , что по условию составляет 5% от численности генеральной совокупности, то , тогда средняя ошибка выборки для средней величины:

.

Предельная ошибка для средней величины рассчитывается по формуле:

,

где		средняя ошибка выборки для средней величины;
		коэффициент доверия;

Коэффициент доверия принимается в зависимости от уровня доверительной вероятности и числа степеней свободы. Для малой выборки (меньше 30 единиц) определяется по таблице Стьюдента.

При заданной вероятности и числа степеней свободы , табличное значение . Тогда, предельная ошибка для средней величины:

.

Доверительный интервал для средней величины генеральной совокупности:

,

где		средняя величина факторного признака выборочной совокупности;
		средняя величина факторного признака генеральной совокупности;
		предельная ошибка средней величины факторного признака;

,

.

Следовательно, с вероятностью 0,95 можно гарантировать, что средняя величина ОПФ в расчете на один предприятие по генеральной совокупности будет находиться в пределах от до

Средняя ошибка выборки доли предприятий, у которых ОПФ превышает среднюю величину, для бесповторного отбора:

,

где		дисперсия доли предприятий выборочной совокупности;
		численность единиц выборочной совокупности;
		численность единиц генеральной совокупности;

.

Предельная ошибка доли предприятий рассчитывается по формуле:

,

где		средняя ошибка выборки доли предприятий,
		коэффициент доверия.

Коэффициент доверия при вероятности по таблице Стьюдента уже был определен, и он составляет . Тогда, предельная ошибка доли:

.

Доверительный интервал для доли предприятий в генеральной совокупности:

,

где		доля предприятий по выборочной совокупности;
		доля предприятий по генеральной совокупности;
		предельная ошибка доли.

.

Следовательно, с вероятностью 0,95 можно гарантировать, что доля предприятий, у которых величина ОПФ больше среднего значения, по генеральной совокупности будет находиться в пределах от до .