1. Квадратное уравнение. Полное, неполное квадратное уравнение. Исследование корней квадратного уравнения в зависимости от знака дискриминанта.

Квадратным уравнением называется уравнение вида

                  ,

где

x - переменная,

a,b,c - постоянные (числовые) коэффициенты.

В общем случае решение квадратных уравнений сводится к нахождению дискриминанта: 

 

Формула дискриминанта:

.

       О корнях квадратного уравнения можно судить по знаку дискриминанта (D) :

• D>0 - уравнение имеет 2 различных вещественных корня

• D=0 - уравнение имеет 2 совпадающих вещественных корня

• D<0 - уравнение имеет 2 мнимых корня (для непродвинутых пользователей - корней не имеет)

В общем случае корни уравнения равны:

                  .

Очевидно, в случае с нулевым дискриминантом, оба корня равны

                  .

Если коэффициент при х четный, то имеет смысл вычислять не дискриминант, а четверть дискриминанта:

                

В таком случае корни уравнения вычисляются по формуле:

                

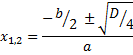
Теорема Виета.

Приведенным квадратным уравнением называется уравнение вида

                 ,

то есть квадратное уравнение с единичным коэффициентом при старшем члене.

В этом случае целесообразно применять теорему Виета, которая позволяет получить относительно корней уравнения следующую систему уравнений:

                  .

ax² + bx = 0, a≠0, b≠0

Пусть неполное квадратное уравнение имеет вид  , где a ≠ 0; b≠ 0. В левой части этого уравнения есть общий множитель  .

1. Вынесем общий множитель   за скобки.

Мы получим  . Произведение равно нулю, если хотя бы один из множителей равен нулю. Поэтому получаем   или  . Таким образом, данное уравнение эквивалентно двум уравнениям:

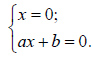
2. Решаем получившуюся систему уравнений.

Решив эту систему, мы получим   и  . Следовательно, данное квадратное уравнение имеет два корня  и  .

 

Существование корней квадратного уравнения

Для того чтобы квадратное уравнение ах² + bх + с = 0 имело корни необходимо и достаточно чтобы дискриминант уравнения был больше или равен нулю. Как правило, в случае необходимости доказать, что заданное квадратное уравнение имеет решение, начинают с вычисления его дискриминанта, с тем чтобы затем доказать его неотрицательность. Но существуют способы, которые основываются на очевидных графических соображениях. Так, если а > 0, то для доказательства того, что уравнение ах² + bx + с = 0 имеет два решения, достаточно указать одну точку х₀, в которой f(x₀) = ах₀² + bx₀ + c < 0. Чаще всего в качестве х₀ берут 0 (даёт достаточное условие с < 0), 1 (условие а + b + с < 0) или – 1 (условие а – b + c < 0).

2. Равносильность уравнений и неравенств. Основные приемы решений.

Два уравнения ( неравенства) называются равносильными, если совпадают множества всех их решений или они оба не имеют решений. Из определения равносильности следует, что вместо того, чтобы решать данное уравнение (неравенство), можно решать уравнение (неравенство), ему равносильное.

Пример 1.

Уравнение x=1 равносильно уравнению x=1, так как число 1 является корнем каждого уравнения, а других корней ни одно из этих уравнений не имеет.

Уравнения x(x-1)=0 и x(x-1)(x-2)=0 не являются равносильными, т.к. число x=2 - корень второго уравнения, но не корень первого.

В определении равносильности не сказано об ОДЗ уравнений, т.е. равносильные уравнения могут иметь различные области допустимых значений.

При решении уравнений вместо понятия равносильности проще использовать понятие равносильности на множестве: два уравнения (неравенства) называются равносильными на множестве А, если совпадают множества всех их решений, принадлежащих множеству А, или они оба не имеют решений на множестве А.

Уравнения (неравенства) могут быть равносильными на некотором множестве, но не быть равносильными. Например: уравнения x=1 и |x|=1 равносильны на множестве всех неотрицательных чисел, но не равносильны.

Уравнение (неравенство) равносильно данной совокупности уравнений (неравенств, систем) на множестве А, если множество всех корней уравнений (неравенств), принадлежащих А, совпадает со множеством всех решений совокупности уравнений (неравенств, систем), принадлежащих множеству А.

Пример 2.

Уравнение (x²+x+1)(3x+4)(-7x+2)(2x-5)(-12x-16)=0 равносильно совокупности уравнений: 3x+4=0, -7x+2=0, 2x-5=0, 12x+16=0 на множестве всех действительных чисел: т.к. x²+x+1>0 при любом x, то данное уравнений равносильно уравнению (3x+4)(-7x+2)(2x-5)(-12x-16)=0. Любой корень этого уравнения обращает в нуль хотя бы один из входящих в него многочленов, т.е. является корнем хотя бы одного из уравнений данной совокупности. Наоборот, проверкой убеждаемся, что любой корень совокупности удовлетворяет данному уравнению. Поэтому уравнение и данная совокупность уравнений равносильны.

Если для данной пары уравнений любой корень первого уравнения является корнем второго уравнения, то второе уравнение называют следствием первого. Если заменить уравнение его следствием, то множество решений второго уравнения будет содержать все корни исходного уравнения и помимо них может содержать еще некоторые числа, называемые посторонними корнями данного уравнения.

Утверждения о равносильности [6].

1. Уравнения f(x)=g(x) и f(x)-g(x)=0 равносильны.

2. Уравнения f(x)=g(x) и f(x)+=g(x)+ равносильны для любого числа .

3. Уравнения f(x)=g(x) и f(x)=g(x) равносильны для любого числа  0.

4. Уравнения a^f(x) =a^g(x) и f(x)=g(x) равносильны для любого числа a>0, a 1.

5. Если функции y=f(x) и y=g(x) неотрицательны на некотором множестве А. Тогда

уравнения f(x)=g(x) и fⁿ(x)=gⁿ(x) равносильны на этом множестве.

6. Если функции y=f(x) и y=g(x) положительны на некотором множестве А. Тогда

уравнения f(x)=g(x) и log_af(x)=log_ag(x) равносильны на этом множестве.

7. Пусть функция y=(x) определена и не обращается в ноль ни в одной точке множества А, содержащемся в ОДЗ уравнения f(x)=g(x). Тогда на множестве А уравнения f(x)=g(x) и f(x)(x)=g(x)(x) равносильны на этом множестве. Множество А может совпадать с ОДЗ исходного уравнения.

Утверждения о равносильности неравенств [6].

1. Неравенства f(x)<g(x) и g(x)<f(x) равносильны.

2. Неравенства f(x)<g(x) и f(x)-g(x)<0 равносильны.

3. Неравенства f(x)<g(x) и f(x)+(x)<g(x)+(x) равносильны если функция (x) определена на ОДЗ неравенства f(x)<g(x).

4. Неравенства f(x)<g(x) и (x)f(x)<(x)g(x) равносильны, если (x)> 0 при всех x из ОДЗ неравенства f(x)<g(x). Неравенства f(x)<g(x) и (x)f(x)>(x)g(x) равносильны, если (x)< 0 при всех x из ОДЗ неравенства f(x)<g(x).

5. Неравенства и f(x)g(x)>0 равносильны.

6. Неравенства и f(x)>g(x) равносильны для любого фиксированного числа a из промежутка (1; ).

7. Неравенства и f(x)<g(x) равносильны для любого фиксированного числа a из промежутка (0;1).

8. Если функции f(x) и g(x) неотрицательны на множестве A. Тогда неравенства f(x)<g(x) и (f(x))ⁿ<(g(x))ⁿ равносильны на этом множестве (n - натуральное число).

9. Неравенства и f(x)<g(x) равносильны (n - натуральное).

10. Неравенства f²ⁿ(x)<g²ⁿ(x) и |f(x)|<|g(x)| (n - натуральное) равносильны.

11. Пусть a - фиксированное число из промежутка (1; ) и функции f(x) и g(x) положительны на некотором множестве A, тогда на этом множестве равносильны неравенства f(x)<g(x) и log_af(x)<log_ag(x). Если a - фиксированное число из промежутка (0;1) и функции f(x) и g(x) положительны на некотором множестве A, тогда на этом множестве равносильны неравенства f(x)<g(x) и log_af(x)>log_ag(x).