1. Дати характеристику основних понять статистики: Статистична закономірність, статистична сукупність.

 Статистична закономірність – це певна послідовність або повторюваність явищ, яка формується та чітко проявляється в масових процесах, при дослідженні достатньо великої кількості одиниць сукупності .

Статистична сукупність – достатньо велика кількість елементів або явищ, котрі поєднуються певними зв'язками та мають як спільні (загальні), так й індивідуальні риси або властивості.

2. Яка величина називається випадковою?

Випадкова величина - це величина, яка в результаті випробувань може приймати певні значення (із сукупності своїх значень) з певноюймовірністю. 

3. Як розрізняють показники за способом обчислення?

Первинні, Похідні

4. Поділ показників за ознакою часу.

Інтегральні, Моментні

5. Поділ показників за формою виразу.

Абсолютні, Відносні, Середні

6. Види середніх ступеневих

Середньо-арифметичне, Середнє квадратичне, Зважене середнє арифметичне, Середнє геометричне

7. Види структурних ступеневих

Мода, Медіана

8. Що називається дискретною і безперервною випадковими величинами?

Дискретна випадкова величина - це випадкова величина, множина значень якої не більш ніж зчисленна.

Випадкова величина, яка приймає всі значення з деякого інтервалу, називається безперервною.

9. Що таке статистичний ряд?

Статистичний ряд- це сукупність випадкових величин отриманих за одинакових умов проведення.

10. Що називається статистичною сукупністю?

Статистична сукупність – достатньо велика кількість елементів або явищ, котрі поєднуються певними зв'язками та мають як спільні (загальні), так й індивідуальні риси або властивості.

11. Форми зображення статистичної сукупності.

Таблична, графічна ( полігон, гістограма, кумулята, огіва), інтегральний варіаційний ряд, емпіричний.

12. Як визначається число груп ( інтервалів) в статистичній сукупності?

Число інервалів визначається за формулою Стерджесса:

K=1+3,222 lg n

13. Які ви знаєте способи вибору? Дайте характеристику кожної з них.

А) простий випадковий відбір здійснюється за допомогою жереба або таблиці випадкових чисел; Б) механічний полягає в тому, що всю генеральну сукупність механічно розділяють на стільки груп, скільки об’єктів повинно увійти до вибірки; В) типовий представляє собою спосіб виконання вибірки з урахуванняи особливостей генеральної сукупності; Г) серійний-при цьому об’єкти з генеральної сукупності вибираються не по одинці, а серіями, які піддаються обстеженню; Д) комбінований при якому поєднуються різні методи.

14. Що називається генеральною сукупністю?

Генеральна сукупність – це нескінченне або скінчене та досить велике число елементів чи компонентів, що складається з якісно однорідних показників.

15. У чому полягає відмінність генеральної сукупності від вибірки?

Сукупність – це будь-яка частина генеральної сукупності відібрана за певними правилами, яка характеризує генеральну сукупність.

16. Що називається рядом розподілу випадкової величини?

Ряд розподілу – це ряд цифрових показників, отриманих в результаті розподілу, які характеризують розподіл одиниць досліджуваної сукупності за варіюючою ознакою.

17. Види графічного зображення рядів розподілу.

Полігон, гістограма, кумулята, огіва, крива.

18. Що таке емпіричний і теоретичний розподіли?

Емпіричний- в основі розподілу певні певні математичні закономірності, які у генеральній сукупності характеризуються деякими нормальними розподілами.

Теоретичний розподіл-розподіл ймовірності, оскільки реальне середнє арифметичне наближається до теоретичного середнього арифметичного.

19. Що таке крива розподілу і що вона показує?

Крива розподілу використовується для графічного зображення дискретних та атрибутивних рядів розподілу. Це лінійний графік, при цьому по осі Х відкладаються значення варіант, а по осі У – частоти. 

20. Які ви знаєте види середніх величин?

Середнє арифметичне, середнє геометричне, середня гармонічна, середнє квадратичне, середнє степеневе.

21. Що називається середнім геометричним значенням і як воно співвідноситься з середньою арифметичною величиною?

Сере́днє геометричне (середнє пропорційне) двох чисел дорівнює квадратному кореню із їхнього добутку. Середнє геометричне не перевищує середнє арифметичне.

22. Формули для визначення середньої арифметичної та зваженої середньої арифметичної величини?

;

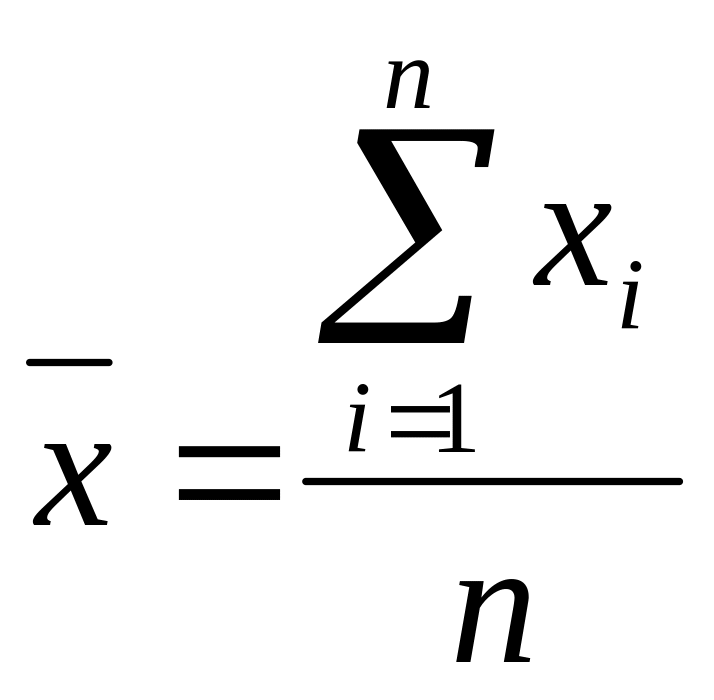23. Що таке середня степенева та її види?

Среднє степеневе— узагальнення середнього арифметичного, середнього геометричного, середнього квадратичного, середнього гармонічного.

24. Що називається модою випадкової величини і як її визначити?

Модою називається найвірогідніша в даному статистичному ряді величина

M₀=X+3(M_e –X)

25. Що називається медіаною? Як вона визначається?

Медіаною називається середнє значення ознаки, у ранжированому варіаційному ряді, тобто значення ознаки рівновіддалене від початку і кінця варіаційного ряду.

M_e=X_m+1 (непарне)

M_e=1/2(X_m+ X_m+1)

26. Що таке частка? Привести приклад частки.

Частка ознаки-це відношення чисельності кожного з членів ряду f₁,f_2,f_3…f_n до чисельності сукупності n, тобто частість або емпірична імовірність появи даної ознаки в сукупності, що вивчається.

27. Що називається дисперсією? Властивості дисперсії.

Дисперсія - частка від ділення суми квадратів відхилень на число всіх вимірів без одиниці і служить мірою розсіювання результатів дослідження відносно середнього арифметичного

28. Що називається середнім квадратичним відхиленням? Призначення розрахункової формули.

Стандартне (середньоквадратичне відхилення s²) характеризує мінливість значень в межах вибірки . Чим більші значення s і s², тим більша мінливість і більше розсіяні біля середньої індивідуальні значення ознаки.

29. Що називається коефіцієнтом варіації і як він розраховується?

Коефіцієнт варіації (V) визначається як відношення стандартного відхилення до середнього арифметичного, виражене у відсотках: ;

30. Вкажіть основні особливості та формулу нормального закону розподілу.

А) будь-яке перетворення початкової випадкової величини Х з нормальним законом розподілу зберігає його; Б) якщо площу обмежену кривою нормального розподілу прийняти за 100%, то можна розрахувати між кривою і будь-якими 2 ординатами; В) встановлено, що площа між ординатами проведеними на відстані Ϭ з обох сторін у нормального розподілу становить 68,3% всіх досліджуваних частот; Г) площа, між ординатами Х_{середнє}=+-2 Ϭ становить 95,4% всіх одиниць сукупності Д) площа обмежена ординатами Х_{середнє}=+-3 Ϭ становить 99,7% всіх одиниць сукупності; Е) площу відмежовану на t стандартних відхилень виражених у % від всієї площі називається статистичною надійністю або рівнем ймовірності (Р), тобто можливість появи ознаки в області Х=+- t Ϭ; Є) ймовірність того, що значення варируваної ознаки знаходиться знаходиться поза вказаними межами називається рівнем значущості.

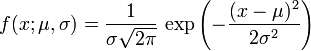
31. Що таке рівень значущості й довірча ймовірність?

Ймовірність того, що значення варируваної ознаки знаходиться знаходиться поза вказаними межами називається рівнем значущості.

Довірча ймовірність –це значення, яким можна довіряти і використовувати. ( 95% і 99%)

32. Як здійснюється вибір рівня значущості? Поняття про довірчі границі.

Рівнем значущості вважається таке достатньо мале значення, яке характеризує практично неможливу подію. Поява такої рідкісної події вказує на невірність прийнятої нульової гіпотези з ймовірністю, що не перевищує вибраний рівень значущості. У вузькому значенні під рівнем значущості розуміється ймовірність події, яку вирішено нехтувати в даній галузі дослідження.

33. Що таке число ступенів свободи?

Число ступенів свободи-це кількість варіантів, які можуть приймати значення функціонально непов’язані одне з одним.

34. Нормальний розподіл. Його суть. Формула визначення.

У теорії ймовірності доведено, що сума різних незалежних випадкових доданків (незалежно від їх закону розподілу) виявляється випадковою величиною, розподіленою згідно нормальному закону (так звана центральна гранична теорема). Тому нормальний розподіл добре моделює найширший круг явищ, для яких відомо, що на них впливають декілька незалежних випадкових чинників.

35. Суть критерію Стьюдента. Його призначення.

t-критерій Стьюдента — загальна назва для класу методів статистичної перевірки гіпотез (статистичних критеріїв), заснованих на порівнянні з розподілом Стьюдента. Найчастіші випадки застосування t-критерію пов'язані з перевіркою рівності середніх значень у двох вибірках

36. Дайте поняття критерію Фішера. Призначення критерію Фішера.

Суть кутового перетворення Фішера полягає у переводі відсоткової частки у величину центрального кута, який вимірюється в радіанах. Критерій  -Фішера призначений для співставлення двох вибірок за частотою, з якою зустрічаються ефект, що цікавить дослідника.

37. Види асиметричного розподілу.

Додатній і від’ємний.

38. Причини асиметричного розподілу.

А) неправильно взята вибірка, коли до неї непропорційно багато чи мало ввійшло представників збільшення чи зменшення значень; Б) дія певних факторів, що зміщують варирувані ознаки в ту чи іншу сторону.

39. Вирівнювання емпіричних кривих за законом нормального розподілу.

Крива нормального розподілу має точки перегину при X ± 1. Якщо уявити графічно, то між X=+l і 1=-1 знаходиться 0,683 частини всієї площі кривої (тобто 68,3%). У границях X=+2 і X- 2. знаходяться 0,954 площі (95,4 %), а між X=+3 і X= - 3 - 0,997 частини всієї площі розподілу (99,7%). На рис. 13 проілюстрований характер нормального розподілу з одно-, дво- і трисигмовою границями.

40. Оцінка різниці генеральних середніх.

Генеральна середня рівна математичному сподіванню випадкової величини. При збільшенні об’єму вибірки n вибіркова середня прямує до генеральної середньої. Це означає, що незміщеною оцінкою генеральної середньої служить вибіркова середня, іншими словами математичне сподівання від вибіркової середньої рівне генеральній середній.

41. Суть дисперсійного аналізу.

Оцінка впливу факторів на мінливість середніх значень досліджуваного явища є основою дисперсійного аналізу, тобто він дає можливість з певною долею достовірності виявити вплив окремого фактора чи сукупності.

42. Види дисперсійних комплексів.

Ріномірні і Нерівномірні.

43. Факторна ( міжгрупова) дисперсія та її визначення.

Факторна (міжгрупова) дисперсія (Sx) – сума зважених квадратів центральних відхилень часткових середніх по градаціях (або по групах) від загального середнього по всьому комплексу.

;

44. Випадкова дисперсія та її визначення.

Випадкова дисперсія (Sz) – сума квадратів центральних відхилень кожної градації від своєї часткової середньої:

;

45. Загальна дисперсія та її визначення.

Загальна дисперсія (Sy) – сума квадратів центральних відхилень від загального середнього по всьому комплексу: ;

46. Розрахунок показників сили та достовірності впливу в однофакторному дисперсійному комплексі.

На основі обчислених дисперсій одно факторного комплексу розраховуємо показник сили впливу:

;

Його помилка буде рівною:

;

Показник достовірності впливу обчислюється за формулою:

47. Розрахунок показника сили впливу за відношенням варіанс.

Показник достовірності впливу у цьому випадку визначають на основі статистичного критерію Фішера за формулою:

при ;

48. Яка головна мета кореляційного аналізу? У чому полягає суть кореляційного аналізу?

Отже, кореляційний зв'язок - це не точна залежність однієї ознаки від іншої, а тому він може мати різний ступінь вираженості - від повної незалежності, до повної кореляції. Під час вивчення кореляційних зв'язків виникає необхідність визначити їхню форму, напрямок і ступінь вираженості.

49. Дайте поняття функціональній, кореляційній і стохастичній залежностям.

Коли кожному значенню першої ознаки відповідає єдине значення другої ознаки, такі зв'язки називаються функціональними.

Коли кожному значенню величини X відповідає не одне. а декілька значень величини Y такі зв'язки називаються стохастичними або кореляцыйними.

50. Які зв’язки називаються прямими, зворотними, лінійними, криволінійними?

За напрямком зв’язок буває прямим, коли залежна змінна збільшується із збільшенням факторної ознаки; та зворотнім, при якому зростання факторної ознаки спричиняє зменшення результату.

За своєю аналітичною формою зв’язки бувають лінійними та нелінійними. В першому випадку між ознаками проявляються в середньому лінійні співвідношення. Нелінійний взаємозв’язок виражається нелінійною функцією, а змінні пов’язані між собою в основному нелінійно.

51. Що служить показником ступеня прямолінійного зв’язку?

Y=a+b*x

Параметр b називається коефіцієнтом регресії і, наскільки загалом відхиляється величина результативного ознаки у при відхиленні величини факторного ознаках однією одиницю.

52. Опишіть основні правила побудови графічних залежностей.

А) Масштаб координатних осей на графіку по можливості повинен бути простим; Б) Основний потік точок повинен іти якомога ближче до лінії з кутом 45°. В) Ціна найменшого розподілу повинна бути більше значення погрішності досліджуваної величини; Г) Масштаб повинен бути не великим і не малим для даного розподілу.

53. Охарактеризуйте прості способи оцінки графічної перевірки залежностей.

До простих графічних методів графічних перевірок відносять метод медіан і зв’язуючого коефіцієнта серединної кореляції. При першому, всі точки ділять вертикальною та горизонтальною лініями. Потім рахують число точко в кожному квадраті. Якщо найбільше число точок в квадраті більше, ніж граничне значення числа точок при заданому рівні значущості, то кореляційний зв’язок між ними існує. Коефіцієнт серединної кореляції обчислюється за формулою:

Кореляційний зв’язок існує, якщо обчислене значення коефіцієнта серединної кореляції більше табличних для заданого числа точок.

54. Основні етапи проведення кореляційного аналізу.

А) оформлення результатів експериментальних досліджень в табличній формі і попередній аналіз взаємозв’язку між змінними величинами; Б) графічний аналіз вихідної географічної інформації або побудова графічної моделі зв’язку і ретельний її розгляд; В) встановлення тісноти взаємозв’язку між змінними величинами; Г) складання математичної моделі кореляційної залежності шляхом підбору параметрів рівняння зв’язку різними способами; Д) оцінка надійності коефіцієнта кореляції , а також всіх параметрів, отриманих кореляційних залежностей.

55. Що таке кореляційне поле?

Для того, щоб приблизно представити форму і тісноту зв'язку, слід побудувати точковий графік, відкладаючи по осях відповідні значення X I Y. Точки на графіку утворять поле кореляції.

56. Що таке коефіцієнт кореляції? Як він обчислюється і що характеризує?

Коефіцієнт кореляції наближено характеризує тісноту зв’язку між ознакам.

57. Які переваги і недоліки мають графічні методи кореляції?

Переваги: а) графічна кореляція наочна і тому лекше розуміється; б) для застосування графічних засобів можна лише небагато знати або зовсім не знати статистичні методи; в) графічні способи не вимагають більшого числа ручних розрахунків, ніж необхідно для аналітичних методів; г) графічна кореляція може приймати будь-яку обгрунтовану форму; д) обмеження області кореляції властиво графічним побудовам, що дозволяє уникнути необгрунтованої екстраполяції при виконанні регресії…Недоліки: а) графічна кореляція не враховує кореляцію між окремими чинниками, що може привести до помилкової кореляції й отримання нестійких результатів; б) графічна кореляція не дозволяє оцінювати значущість окремих чинників; в) графічна кореляція не дає можливості досить повної оцінки отриманих результатів.

58. За допомогою яких показників (коефіцієнтів, індексів) оцінюють тісноту кореляційних зв’язків між кількісними ознаками?

Кореляційне відношення є коренем квадратним з відношення міжгрупової дисперсії до загальної дисперсії ряду.

59. Як визначається кореляційне відношення?

Кореляційне відношення є коренем квадратним з відношення міжгрупової дисперсії до загальної дисперсії ряду.

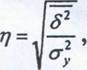
60. Як перевіряється значущість параметрів коефіцієнта кореляції?

Значущість кореляційного відношення оцінюється за t-критерієм Стьюдента. Спочатку розраховується похибка кореляційного відношення, далі визначається фактичне значення критерію істинності. Потім порівнюється розрахункове значення t-критерію Стьюдента з табличним при даному числі ступенів свободи і заданому рівні значущості.

61. Яке призначення регресійного аналізу?

Коефіцієнт кореляції не дає змоги оцінити, як кількісно змінюється результуюча ознака зі зміною факторної на одиницю виміру. У цьому випадку доцільно використати регресійний аналіз, що дає змогу визначити форму кореляційної залежності, яка виражається рівнянням прямої лінії.

62. Що характеризує коефіцієнт регресії?

Як кількісно змінюється результуюча ознака зі зміною факторної на одиницю виміру.

63. Як перевіряється значущість параметрів рівняння регресії?

Іноді значущість оцінюють шляхом перевірки коефіцієнта r_sf з критичним значенням r_sr:

Інший спосіб оцінки достовірності полягає у використанні t-критерію Стьюдента.

64. Як обчислюється коефіцієнт лінійної регресії?

Для обчислення параметрів рівняння регресії а₀ та а₁ складають і розв’язують систему рівнянь:

Можна використати й інші формули, що отримують з методу найменших квадратів, наприклад:

65. У чому відмінність лінійної регресії від криволінійної?

Лінійна регресія виникає при лінійній залежності між змінними, тобто їх залежність можна записати за допомогою лінійного рівняння. Криволінійна регресія виникає, коли мале значення коефіцієнту кореляції вказує тільки на відсутність лінійного зв'язку між величинами. Але при цьому може існувати інший нелінійний зв' язок і бути досить тісним.

66. Якими показниками можна виміряти взаємну зв’язаність альтернативних ознак?

67. Суть поліхоричного показнику зв’язку.

Поліхоричний показник зв’язку використовується для того, щоб порівняти 2 явища, одне з яких має кількісну, а друге якісну характеристики.

68. Формула для визначення поліхоричного показнику зв’язку.

;

69. У чому полягає особливість методики визначення коефіцієнта асоціації Юла ( тетрахоричного показника зв’язку)?

Якщо кількість градацій явищ дорівнює двом: наявність чи відсутність, додатні чи від’ємні значення явищ, то у такому випадку за формулою Юла обчислюють тетрахоричний показник зв’язку.

70. Формула для визначення тетрахоричного показнику зв’язку

;

71. Оцінка достовірності тетрахоричного показнику зв’язку.

72. Що таке частинний коефіцієнт кореляції?

Для визначення тісноти зв'язку між двома ознаками, якщо значєння третьої є сталим використовують частковий коефіцієнт кореляції.

73. Формула для визначення частинного коефіцієнта кореляції.

;

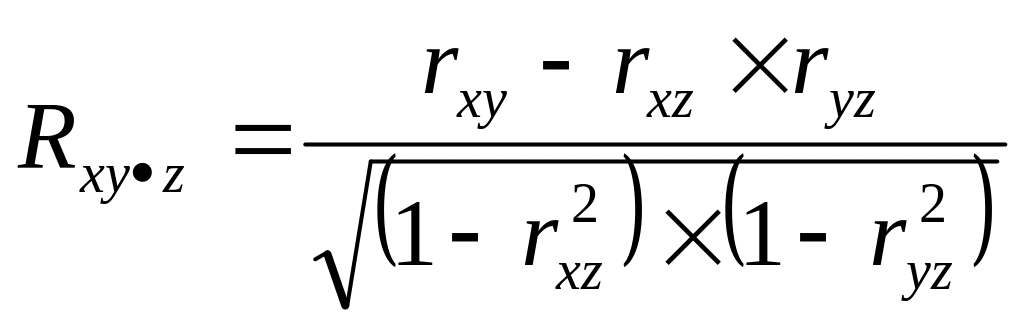74. Що показує множинний коефіцієнт кореляції і які умови його застосування?

Для комплексної оцінки ступеня зв'язку між явищем Y і факторами, що його обумовлюють (X, Z) використовують коефіцієнт множинної кореляції.

75. Який зміст має коефіцієнт множинної кореляції і як він пов’язаний з парним коефіцієнтом кореляції?

Кожен із парних коефіцієнтів не може перевищувати за абсолютним значенням значення коефіцієнта множинної кореляції.

76. Формула для визначення множинного коефіцієнта кореляції. ;

77. Оцінка достовірності множинного коефіцієнта кореляції.

Ступінь достовірності коефіцієнта множинної кореляції оцінимо за F-критерієм Фішера:

;

78. Висловіть схему визначення параметрів рівняння лінійного зв’язку множинної регресії.

Коефіцієнт показує, на скільки збільшується значення з кожним збільшенням величини і при сталому значенні , - збільшення значення внаслідок зміни на одиницю при сталому значенні , - загальний початок відліку.

79. Які особливості використання й інтерпретації рівнянь множинної регресії?

Рівняння регресії як для парної так і для множинної кореляції доцільно розраховувати і будувати тільки тоді, коли тіснота зв’язку є досить високою.

80. Коли множинну регресію називають лінійною?

Множинна регресія вивчає зв’язок між трьома або більше ознаками та має наступний вигляд:

,

81. Класифікація поняття «інформація».

А) Одинична інформація :

1. інформація-повідомлення (словесне, письмове, жестом);

2. інформація-сигнал (повідомлення, що викликає наслідки, які перевищують розміри сигналу);

Б) Групова інформація (зняття невизначеності про стан масового явища).

82. Показник визначення кількості інформації.

Біт

83. Що таке ентропія, що вона характеризує і її властивості?

Ентропія-міра невизначеності системи. Вона характеризується таими власивостями: при N=1, вона перетворюється в 0; із зростанням числа N функція неперервно збільшується, досягаючи максимуму у випадку рівності ймовірностей; при N=0 показник ентропії також рівний 0.

84. Абсолютна і відносна ентропія. Коефіцієнт впорядкованості.

85. Поняття про інформаційний коефіцієнт взаємної відповідності.

Коефіцієнт взаємної відповідності характеризує ступінь взаємної відповідності контурів. ( у % чи долях одиниці). Інформаційний коефіцієнт взаємної відповідності дозволяє оцінити взаємну відповідність між явищами, які мають на картах якісну або кількісну характеристики, при однаковому або рівному числі співставлених контурів.

86. Методика визначення коефіцієнта взаємної відповідності.

87. Поняття «поле» і «карти полів». Їх використання при геоморфологічних дослідженнях.

Поле (фізичне) – область поширення сил, енергії в кількісному вигляді.

Поле (математичне) – область поширення величин.

Поле ( загальне) – область поширення будь-яких явищ.

Карти полів статики – це карти, які показують стан досліджуваного явища поелементно на певний момент чи проміжок часу.

88. Статистичні поверхні. Карти статистичних поверхонь.

Статистична поверхня – це поверхня, на якій кожна точка ділянки характеризується певною величиною певної кількісної ознаки.

Сукупність дискретно розміщених картографічних знаків при умові їх достатньої масовості в дисперсійності створюють карти статистичних поверхонь.