10. Теорема о выпуклости и точке перегиба

Пусть дважды дифференцируема на .

1) (необходимые условия выпуклости) Если кривая выпукла (вогнута) на , то 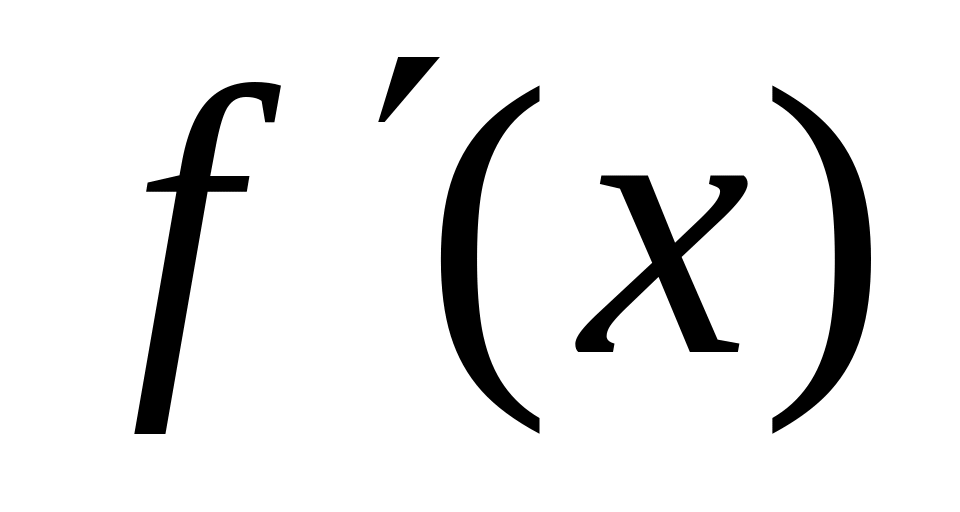не убывает (не возрастает) на и .

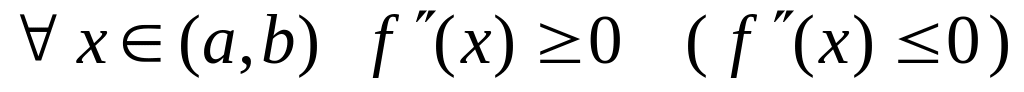2) (достаточные условия выпуклости) Если монотонно возрастает (убывает) на или , то кривая вып (вог) на .

3) (необходимые условия точки перегиба). Если 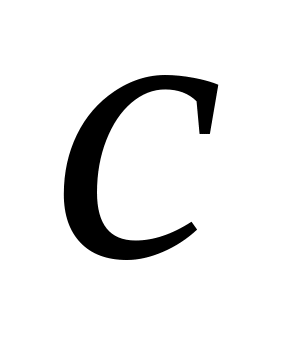- точка перегиба кривой, то .

11. Т. о св-вах неопред. интеграла на отрезке беск. длины

1) 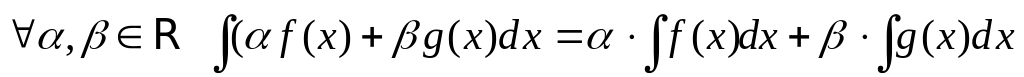, если хотя бы два из трех интегралов существуют.

2) (формула замены переменных) Если

и функция 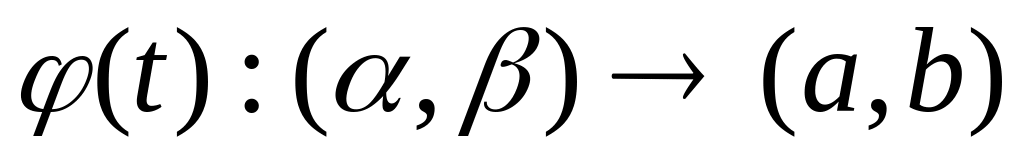непрерывно дифференцируема на 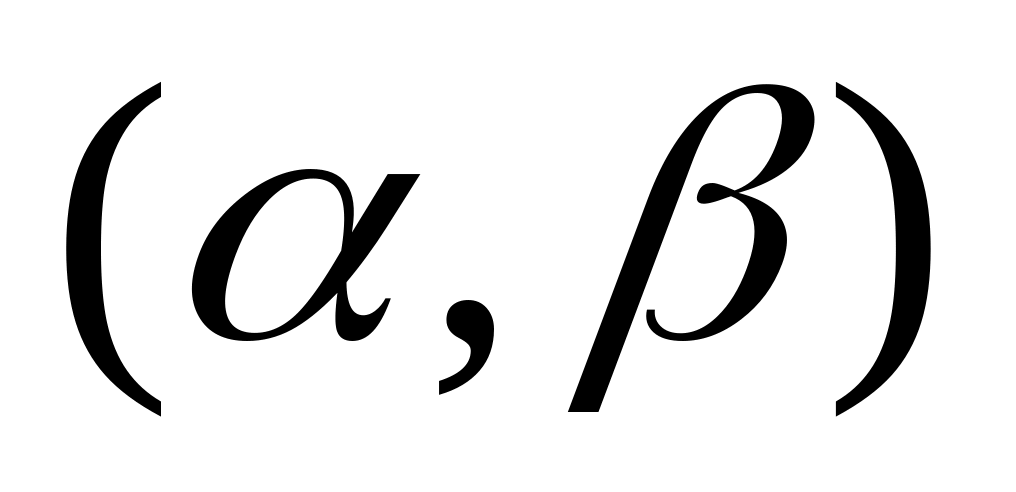, то на существует интеграл функции 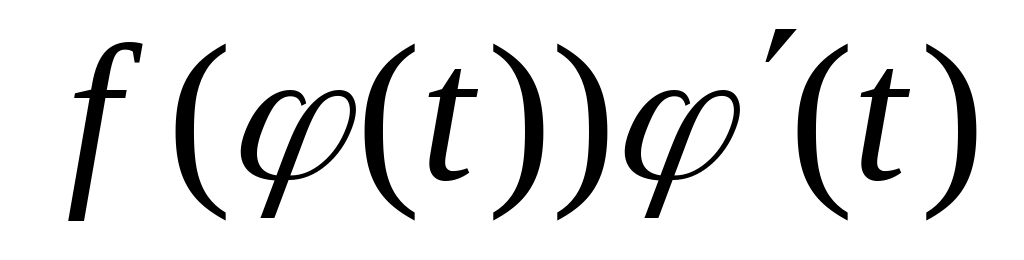и он вычисляется по формуле .

3) (формула интегрирования по частям) Если функции дифференцируемы на , и существует один из интегралов 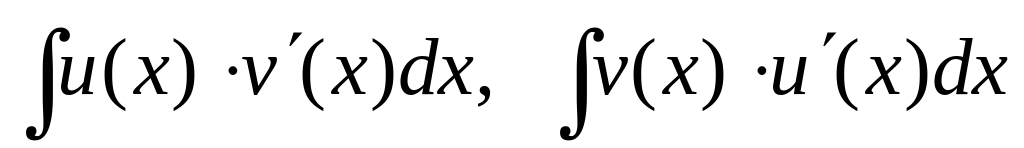, то существует второй интеграл и имеет место равенство .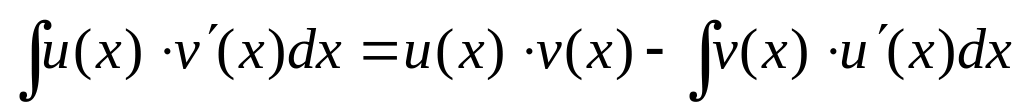

12. Теорема о свойствах определенного интеграла

1) , если хотя бы два из этих интегралов существуют .

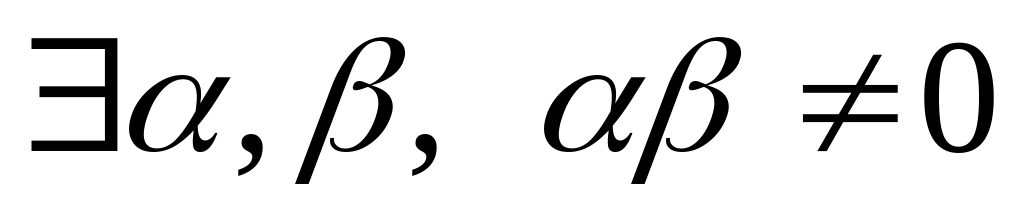2) Если 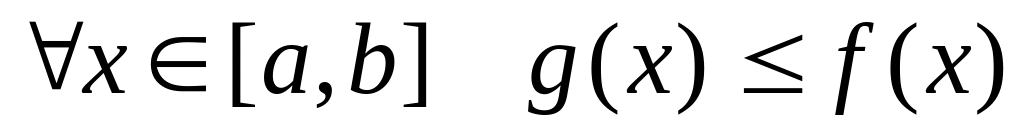, то .

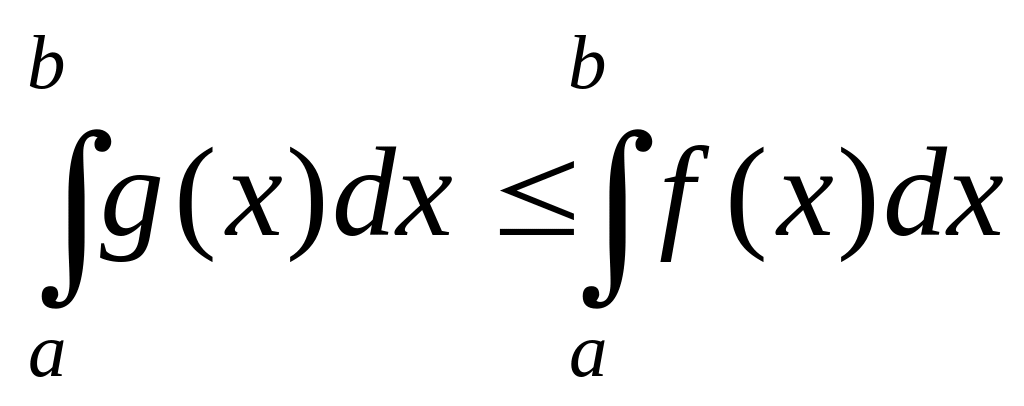3) Если интегрируема на и 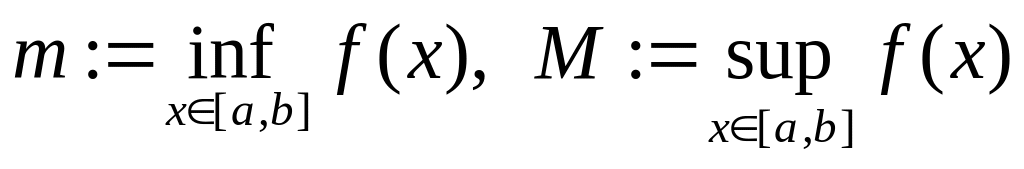, то

4) (теорема о среднем) Если непрерывна, а 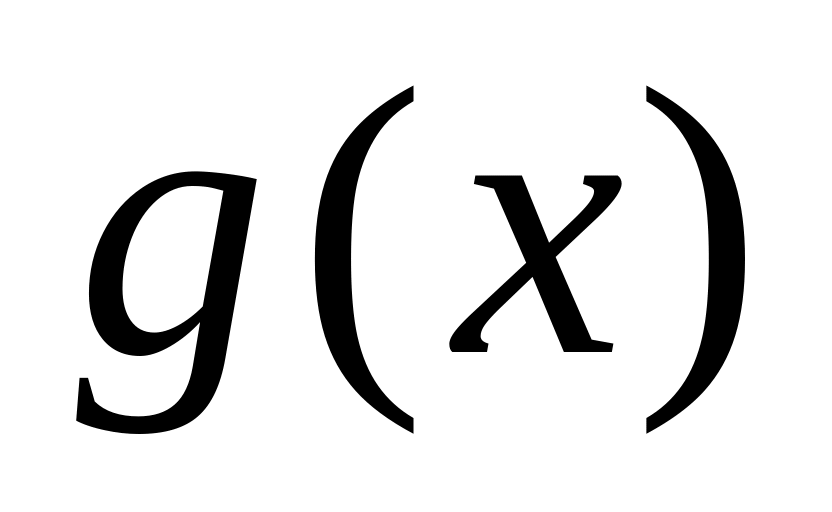знакопостоянна на , то 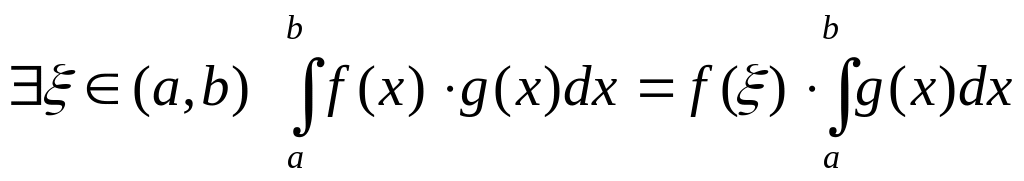при условии существования интегралов.

5) .
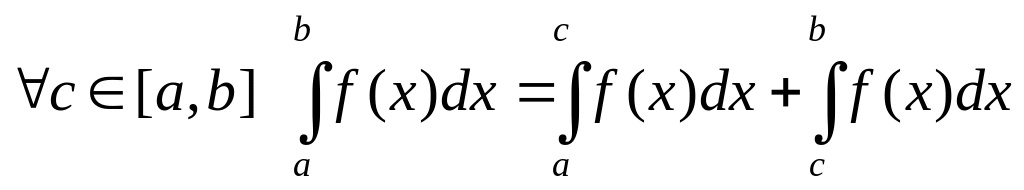