1. Системой линейных алгебраических уравнений (СЛАУ)

называется система уравнений вида , где известные числа , наз коэффициентами СЛАУ; известные числа - свободными членами; неизвестные, искомые числа - решением.

СЛАУ называется совместной, если она имеет хотя бы одно решение. В противном случае СЛАУ несовместна.

СЛАУ называется определенной, если она имеет ровно одно решение и неопределенной, если решений больше одного.

2. Суммой двух матриц р-ра называется матрица

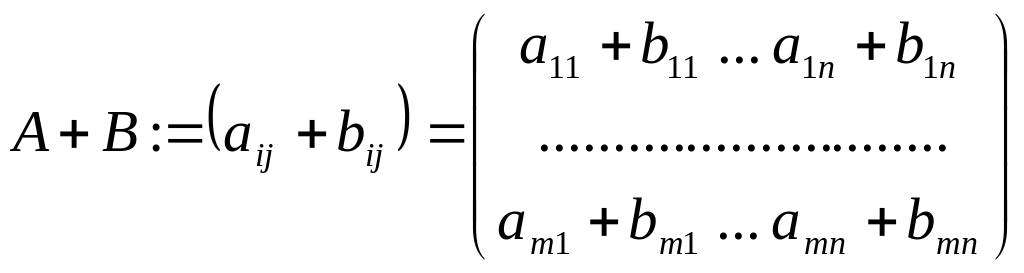
Произведением матрицы на число называется матрица

Произведением матрицы р-ра на матрицу размера называется матрица р-ра , элементы которой вычисляются по правилу

3. Векторным пространством называется множество Е, для элементов которого определены операции сложения и умножения на число, удовлетворяющие следующим аксиомам:

1)

2)

3)

4) ,

5) ,

6) , Множество чисел R

7) ,

8) .

Пример. Нулевое пространство, единственным элементом которого является ноль; Множество чисел R

4. Декартовым произведением множеств   называется множество упорядоченных n-ок вида

Декартовым произведением векторных пространств E и F называется декартово произведение соответствующих множеств , на котором определены операции сложения элементов и умножения их на число по правилу:

, .

Пример. А={2, 3}, B={3, 5, 6}, А В={(2, 3), (2, 5), (2, 6), (3, 3), (3, 5), (3, 6)}

5. Линейной комбинацией элементов называется сумма вида , где - действительные числа, которые называются коэффициентами разложения.

Элементы наз линейно зависимыми, если существует равная нулю линейная комбинация этих элементов, в которой не все коэффициенты равны нулю. В противном случае элементы называются линейно независимыми.

Последовательность элементов наз базисом в векторном пространстве Е если каждый элемент из Е единственным образом представим в виде линейной комбинации этих элементов.

6. Билинейная форма называется скалярным произведением на векторном пространстве , если она обладает свойствами:

1) ;

2) ; 3) .

Отображение , называется нормой, если оно обладает свойствами:1) ;

2) ; 3) .

Пример.

Пример.

7. Отображением множества А в множество В наз правило, сопоставляющее каждому элементу из А один элемент из В. .

Отображение из векторного пространства в векторное пространство F наз. линейным отображением, если .

Пример. - линейный оператор

8. -мерным евклидовым (точечным) пространством называется тройка объектов: -мерное векторное пространство , какое-либо скалярное произведение (x,y) на нём и множество “точек” P, которые согласованы следующим образом:

1) каждой упорядоченной паре точек поставлен в соответствие один элемент , который обозн ;

2) существует единственная точка B со свойством ; 3) .

9. В мерном евклидовом пространстве совокупность каких-либо точки и базиса наз ДСК

Полярной системой координат в называется совокупность точки O(-полюс) и луча с началом в этой точке (-полярная ось).

10. Символом Кронекера называется отображение , определяемое по правилу , если и , если .

Базис наз ортонормированным, если .

ДСК, в которой выделенный базис является ортонормированным, называется ПДСК.

11. Коэффициенты разложения элемента по базису , наз компонентами вектора

Радиус-вектором точки M и ПДСК наз вектор .

Координатами точки в ПДСК называются компоненты её радиуса-вектора .

12. Упорядоченная тройка некомпланарных векторов с общим началом называется правой, если из конца вектора C движение от A к B по кратчайшему из двух углов происходит против часовой стрелки.

Векторным произведением называется вектор , который определяется свойствами: 1) ; 2) ; 3) - правая тройка векторов.

13. (физический смысл скалярного произведения) Работой постоянной силы по перемещению материальной точки из начала в конец вектора называется величина .

(физический смысл векторного произведения). Моментом относительно точки силы , приложенной к точке , наз вектор .

14. Смешанным произведением трех векторов называется число .

(геометрический смысл модуля)

1) численно равен площади параллелограмма, построенного на векторах как на сторонах.

2) численно равен объему призмы, построенной на векторах как на ребрах .

15. Плоскостьюв с фиксированной ПДСК называется множество точек, координаты которых удовлетворяют уравнению

через точку

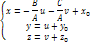
Прямая-множество точек, удовл. системе ур-ий

16. Кривой второго порядка в называется множество точек, координаты которых в какой-либо ПДСК удовл уравнению , где одновременно.

Эллипс – множество точек в , сумма расстояний от каждой и которых до двух заданных точек (фокусов) есть величина постоянная. , где .

17. Гипербола – множество точек в , модуль разности расстояний от каждой из которых до двух заданных точек (фокусов) есть величина постоянная.

, где .

Парабола - множество точек в , расстояния от которых до заданной точки (фокуса) и до заданной прямой (директрисы) совпадают.

18. Характеристическим многочленом матрицы называется многочлен -ой степени .

Корни характеристического многочлена наз. собственными числами матрицы А.

Для собственного числа однородная СЛАУ является совместной, но неопределенной в силу теоремы. Ее ненулевые решения называются собственными векторами матрицы

Пример. Определитель характеристической матрицы представляет собой скалярный многочлен относительно   и называется характеристическим многочленом матрицы  

Пример. Собственные числа:   ,   , соответствующие собственные векторы:   ,   .       

19. Выражение вида где числа , называется числовой последовательностью.

Число называется пределом последовательности при , если Пример. 1) 1,2,..., n,...; 2) 1,-1,1,-1,...,(-1)ⁿ,...; Пример. Пусть x_n = 1/n, покажем, что lim_n1/n = 0.Для этого запишем определение: >0  N:  n>N |x_n|<. То есть 1/n< при n>N=[1/].

20. Числовым рядом называется выражение вида , где

N-ой частичной суммой ряда называется сумма .

Предел называется суммой ряда.

Пример.

21. Объединением множеств наз .

Пересечением множеств наз .

Разностью множеств наз .Пример. X={1,2,3,4,5} и Y={2,4,6,8}, то X∪Y={1,2,3,4,5,6,7,8}

Пример. A={a,b}, B={b,c}, C={a,c}. A∩B∩C=∅, хотя A∩B={b}, B∩C={c}

Пример. X={1,2,3,4,5}, Y={2,4,6,8}, X\Y={1,3,5}, Y\X={6,8}

22. Множество ограничено, если оно ограниченно и сверху и снизу: .

Точной верхней (нижней) гранью множества называется наименьшее (наибольшее) число со свойствами

Примером ограниченного множества является отрезок 

Для множества 

верх ;  низ .

23. Отображение называется инъективным, если она разным элементам из X сопоставляет разные элементы из Y.

Отображение наз сюръективным, если

Отображение называется биективным, если оно инъективно и сюръективно.

Пример.   — инъективно.

Пример.  — сюръективно.

Пример.  — биективная функция из   в  .

24. Композицией отображений и называется отображение , определяемое по правилу .

Сужением отображения f на подмножество называется отображение определяемое по правилу .

Пример. Пусть  , а  ,тогда   является композицией g и f.

25.1) Степенные .

2) Показательные .

3)Логарифмические 

4) Тригонометрические .5) Обр. тригонометр. .

Функция называется элементарной, если она получена из основных элементарных с помощью конечного числа, операций сложения, вычитания, умножения, деления, возведения в степень и композиции.

26. Гиперболические функции, функции, определяемые формулами:

Рациональная функция — это дробь, числителем и знаменателем которой являются многочлены.

Функция Дирихле — функция , принимающая значение 1, если аргумент есть рациональное число, и значение 0, если аргумент есть иррациональное число,

27. Число сочетаний Пример.

e=

28. Предел функции в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.

29. Пусть функция определена на и является предельной точкой X. Говорят, что непрерывна в точке , если = .

Функция называется непрерывной на множестве, если она непрерывна в каждой точке этого множества.

Пример. непрерывна в любой точке .

Пример. непрерывна на множестве

30. Пусть и является предельной точкой. называется точкой устранимого разрыва, если существует конечный и он .

Предел спр Предел сл

Пример. Функция   задаваемая формулой непрерывна в любой точке   Точка   является точкой устранимого разрыва, ибо предел функции

Пример.

Пр:  Лев: 

31. (.) наз точкой разрыва первого рода, если сущ-ют конечные пределы справа и слева, но они различны.

(.) называется точкой разрыва второго рода, если, по крайней мере, один из односторонних пределов не существует или равен бесконечности.

Пример. f(x) =  Функция не определена в точке х = 0, но имеет в ней конечный предел  , т.е. в точке х = 0 функция имеет точку разрыва 1 – го рода. Это – устранимая точка разрыва, т.к. если доопределить функцию:

Пример. Функция f(x) =   имеет в точке х₀ = 0 точку разрыва 2 – го рода, т.к

32. Асимптота — прямая, обладающая тем свойством, что расстояние от точки кривой до прямой стремится к нулю при удалении точки вдоль ветви в бесконечность.

 Касательная - прямая, с которою стремится совпасть секущая, проведенная через две точки на произвольной кривой, по мере сближения этих точек.

(геом смысл производной) График ф-ии имеет касательную в точке ттт, когда имеет производную в .

33. Если дифференцируема в , то слагаемое называется дифференциалом функции .

34. Кривая , то есть функции непрерывно дифференцируемы на и все ее точки неособые.

35. Локальный экстремум – точка, в которой достигается наибольшее(наименьшее) значение функции в некоторой, сколь угодно малой, окрестности точки.

Пример.    - стационарная точка;   для всех x, следовательно, и в точке x=0 - локальный минимум.

36. Кривая выпукла (вогнута) на , если она лежит выше (ниже) любой своей касательной.

Точка , называется точкой перегиба кривой, если эта кривая выпукла (вогнута) на и вогнута (выпукла) на .

37. Многочлен степени называется многочленом Тейлора. Разность - остаточным членом. Формула - формула Тейлора.

38. Пусть функция определена на интервале . Дифференцируемая на функция наз первообр функции , если .

Множество всех первообразных функции называется неопределенным интегралом этой функции.

ЗАМЕЧАНИЕ Если есть первообразная функции на , то любая другая первообразная имеет вид , где - произвольная постоянная.

39. Пусть функция имеет производную порядка в точке . называется нулем кратности S , если

Теорема Гаусса. Многочлен -ой степени , имеет ровно корней, если учитывать кратность каждого корня и все комплексные корни.

Пример. Функция имеет ноль кратности 2 в точке .

; ;

40. Разобьем отрезок точками на попарно непересекающихся отрезков, и обозначим это разбиение . Длина наибольшего из отрез ков , где , называется диаметром разбиения T отрезка .

41. Сумма вида называется интегральной суммой.

Если существует конечный предел , равномерный относительно выбора точек E: ,то он называется определенным интегралом.

42. Пусть на отрезке заданы две функции . Множество точек называется криволинейной трапецией .

Функция Дирихле — функция , принимающая значение 1, если аргумент есть рациональное число, и значение 0, если аргумент есть иррациональное число,

Гребешок Дирихле – частный случай криволинейной трапеции

43. Функция называется кусочно-непрерывной на , если она непрерывна на за исключением конечного числа точек разрыва первого рода.

Функция называется кусочно-монотонной на , если она ограничена и для некоторого разбиения не убывает или не возрастает на каждом интервале .

Пример. кусочно-непрерывная

Пример. кусочно-монотонная

Теорема существования интеграла Римана.

1) Если кусочно непрерывна или кусочно монотонна на , то интеграл существует.

2) Если интеграл существует, то ограничена на .

44. Пусть функция определена на и интегрируема на каждом отрезке . Если существует конечный предел , то он называется несобственным интегралом функции.

Пример.

ТЕОРЕМЫ

1. Теорема о свойствах СЛАУ

1) (критерий Кронекера-Капелли совместности СЛАУ) СЛАУ совместна тогда и только тогда, когда ранг матрицы этой СЛАУ равен рангу расширенной матрицы.

2) (критерий определенности СЛАУ) Для того чтобы СЛАУ была определенной необходимо и достаточно, чтобы она была совместной и ранг матрицы коэффициентов совпадал с числом неизвестных:

3) (формулы Крамера) Определенная СЛАУ с помощью элементарных преобразований приводится к СЛАУ, у которой матрица коэффициентов квадратная и В этом случае решение СЛАУ вычисляется по формулам Крамера где -определитель, получаемый из заменой i-ого столбца на столбец свободных членов.