Линейные отображения векторных пространств

14. Определение линейного отображения, свойства, примеры. Матрица линейного отображения. Ядро и образ линейного оператора. Ранг и дефект.

15. Действия над линейными операторами. Существование обратного оператора.

16. Инвариантные подпространства. Собственные векторы и собственные числа. Характеристический многочлен. Теорема Гамильтона-Кэли.

Билинейные и квадратичные формы

17. Определение, матрицы. Теорема Лагранжа. Закон инерции.

18. Положительно определенные квадратичные формы. Критерий Сильвестра.

19. Приведение квадратичной формы к каноническому (нормальному) виду.

Рекомендуемая литература

Ильин В.А., Позняк Э.Г., Линейная алгебра, М., Наука, 1988.

Беклемишев Д.В., Курс аналитической геометрии и линейной алгебры, М, Наука, 1984.

Канатников А.Н., Крищенко А.П., Линейная алгебра, М., Изд. МГТУ им. Н.Э. Баумана, 1999.

Курош А.Г. Курс высшей алгебры, М., Наука, 1971.

Проскуряков И.В. Сборник задач по линейной алгебре, М., Наука, 1978.

Ефимов А.В., Каракулин А.Ф. и др., Сборник задач по математике для втузов, ч.1, М., Физматлит, 2001

Задание по курсу «Аналитическая геометрия»

1. Вычислить определитель матрицы

Вариант 1 Вариант 2 Вариант 3

2. Решить систему уравнений

Вариант 1	Вариант 2	Вариант 3
x1 + 2x2 + 3x3 + 4x4 = 5	2x1 + 2x2 - x3 + x4 = 4	2x1 + 3x2 + 11x3 + 5x4 = 2
2x1 + x2 + 2x3 + 3x4 = 1	4x1 + 3 x2 - x3 + 2x4 = 6	x1 + x2 + 5x3 + 2x4 = 1
3x1 + 2x2 + x3 + 2x4 = 1	8x1 + 5x2 - 3x3 + 4x4 = 12	2x1 + x2 + 3x3 + 2x4 = - 3
4x1 + 3x2 + 2x3 + x4 = - 5	3x1 + 3x2 - 2x3 + 2x4 = 6	x1 + x2 + 3x3 + 4x4 = - 3

3. Найти обратную матрицу методом элементарных преобразований

Вариант 1

Вариант 2

Вариант 3

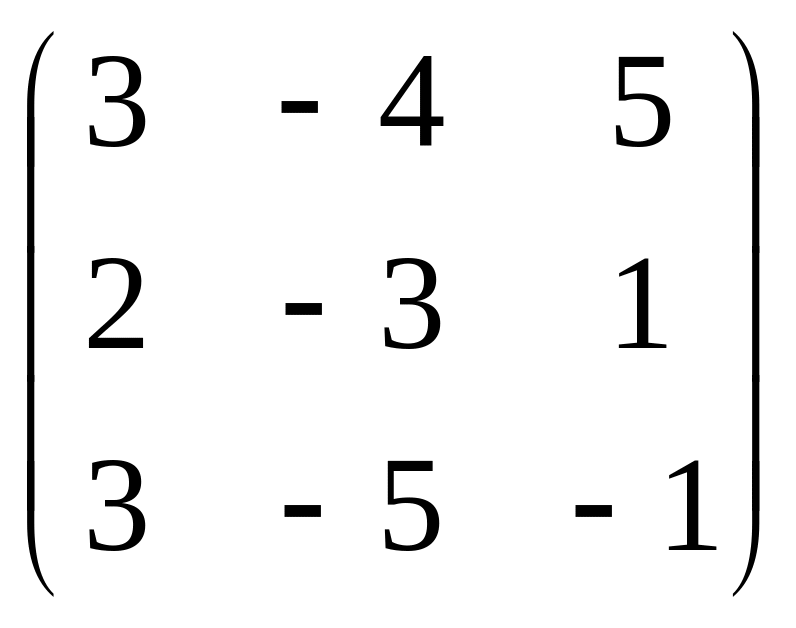
4. Даны три вектора p = {3; -2; 1}, q = {-1; 1; -2}, r = {2; 1; -3}

Найти разложение вектора c по базису p, q, r.

Вариант 1

Вариант 2

Вариант 3

c = {11; -6; 5} c = {9; -6; 4} c = {-7; -7; 5}

5. Даны три некомпланарных вектора a, b, c

Вычислить, при каких значениях λ и μ векторы

	λ a + b + c, a + λ b + c, a + b + λ c компланарны	Вариант 1
	λ a + μ b + c, a + λ b + μc коллинеарны	Вариант 2
	a + b , b + c, a - λ c компланарны	Вариант 3

6. Составить каноническое уравнение прямой

Вариант 1

Вариант 2

Вариант 3

7. Доказать параллельность прямых

Вариант 1

Вариант 2

Вариант 3

x = 4t + 5; y = – 2t + 2; z = 2t – 7;	x = 2t + 5; y = – t + 2; z = t – 7;	x = t + 3; y = t + 4; z = – 2t + 6;
и	и	и

8. Составить уравнение плоскости, проходящей через прямую

Вариант 1	Вариант 2	Вариант 3
параллельно вектору l {2,-1,-2}	и точку М {4,-2,-3}	Перпендикулярно плоскости x – 2y + z + 5 = 0

9. Даны вершины треугольника А (4, 1, - 2); В (2, 0, 0 ); С (-2, 3, -5)

Составить уравнение высоты и найти длину высоты, опущенной из вершины

Вариант 1	Вариант 2	Вариант 3
А	В	С

10. При каких значениях m и n уравнение определяет:

1. Центральную линию;

2. Линию без центра;

3. Линию, имеющую бесконечно много центров.

Вариант 1	x2 + 6xy + my2 + 3x + ny – 4 = 0
Вариант 2	mx2 + 12xy + 9y2 + 4x + ny – 13 = 0
Вариант 3	5x2 + 14xy + my2 + 20x + ny – 18 = 0

11. Привести уравнение к каноническому виду, определить тип уравнения, определить геометрический образ, определяемый уравнением. Построить на чертеже оси первоначальной системы координат, оси систем, которые вводятся по ходу решения, и геометрический образ, определяемый уравнением. Определить параметры кривой (если они существуют): полуоси, эксцентриситет, координаты фокусов, выписать уравнения директрис и асимптот.

Вариант 1	4xy + 3y2 + 16x + 12y – 36 = 0
Вариант 2	3x2 + 10xy + 3y2 – 2x – 14y – 13 = 0
Вариант 3	25x2 – 14xy + 25y2 + 64x – 64y – 224 = 0