ГОСУДАРСТВЕННЫЙ КОМИТЕТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ПО ВЫСШЕМУ ОБРАЗОВАНИЮ
Петрозаводский государственный университет
Кольский филиал
Горно-технический факультет
А.А.Остапенко, Я.А.Сахаров
Методическое пособие по математике
для студентов 1курса заочного отделения
специальности
090200 «Высоковольтные энергетика и электротехника»
180400 «Электропривод и автоматика промышленных
установок и технологических комплексов»
Апатиты
2002
Составители:
доцент кафедры математики,
К.ф.-м.н. Остапенко А.А.
доцент кафедры математики,
К.ф.-м.н. Сахаров Я.А.
Одобрено на заседании кафедры прикладной математики
Протокол № 2 от 05.03.2002 г.
Математический анализ, 1 семестр
Список экзаменационных вопросов
Лектор Остапенко А.А.
Числовые последовательности.
1. Числовые последовательности {}. Операции над ними. Ограниченные и неограниченные {}.
2. Бесконечно большие и малые {}. Осн. св-ва бесконечно малых {}.
3. Сходящиеся {} и их осн.свойства
4. Монотонные {} , число е .
5. Подпоследовательности. Предельные точки {}. Теорема Больцано-Вейерштрасса.
6. Критерий Коши для сходящихся {}
Предельное значение функции.
7. Понятие функции. Предельное значение функции по Гейне. Арифметические операции над функциями, имеющими пределы.
8. Непрерывность функции. Арифметические операции над непрерывными функциями.
9. Два замечательных предела sin(x)/x и (1+1/x)x.
Дифференциальное исчисление.
10. Производная. Ее физическая и геометрическая интерпретация.
11. Дифференцируемость функции. Производные суммы, разности,
произведения и частного.
12. Производные элементарных функций.
13. Производная обратной функции. Производная неявной функции.
15. Дифференцирование сложной функции . Логарифмическая производная.
16. Производные высших порядков. Формула Лейбница.
Дифференцирование параметрической функции
Теоремы о непрерывных и дифференцируемых функциях.
17. Предельное значение функции в смысле Коши.
18. Локальная ограниченность функции, имеющей предельное значение.
19. Устойчивость знака непрерывной .функции.
20. Прохождение через нуль. непрерывной .функции.
21. Ограниченность и достижение своих граней функции, непрерывной на сегменте (Первая и вторая теоремы Вейерштрасса).
22. Локальный экстремум. Теорема Ролля о нуле производной.
23. Формула конечных приращений Лагранжа.
24. Формула Коши конечных приращений.
25. Правило Лопиталя.
26. Формулы Тейлора и Маклорена. Формы остаточного члена.
27. Разложение и асимптотика элементарных функций.
Исследование функций
28. Участки монотонности и точки экстремума функций.
29. Выпуклость и точки перегиба графика функции.
Рекомендуемая литература
Ильин В.А., Позняк Э.Г. Основы математического анализа. М., Наука, 1965.
Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. М., Наука, 1969.
Курант Р. Курс дифференциального и интегрального исчисления. М., Наука, 1967.
Демидович Б.П. Сборник задач и упражнений по математическому анализу. СПб., Мифрил, 1995.
А.М.Тер-Крикоров, М.И.Шабунин. Курс математического анализа, М., МФТИ, 1997.
Вавилов В.В., Мельников И.И. и др. Задачи по математике. Начала анализа: справочное пособие. М., Наука, 1990.
Таблица производных от некоторых функций.
,
где С - постоянная
;
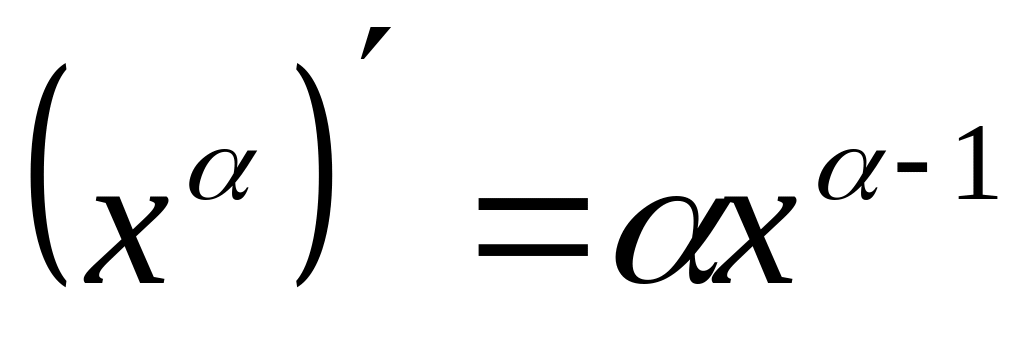Контрольное задание
Вариант 1.
Найти:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
Вариант 2
Найти:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
Вариант 3
Найти:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
Математический анализ , 2 семестр.
Список экзаменационных вопросов