2.2.Регрессионный анализ экономических показателей
С этой целью подбирают класс функций, связывающий результативный показатель Y и аргументы X1, X2, X3 ,... Xk, отбирают наиболее информативные аргументы, вычисляют оценки неизвестных значений параметров уравнения связи и анализируют точность полученного уравнения.
Наиболее часто используется множественная линейная модель регрессионного анализа, уравнение которой имеет вид:
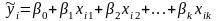
для всех i=1,2,…n, или в матричной форме:
,
Где
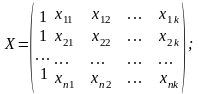
Исследуем на основе линейной регрессионной модели зависимость числа государственных и муниципальных образовательных учреждений, реализующих программы высшего профессионального образования (Y) от уровня образования населения (X1), ожидаемая продолжительность жизни при рождении (X2), общедоступные библиотеки(численность пользователей) (X3) общие коэффициенты рождаемости (X4) и численность обучающихся по программам начального профессионального образования (X5) по регионам России.
Проверка исходных данных на мультиколлинеарность
Одним из основных препятствий эффективного применения множественного регрессионного анализа является мультиколлинеарность. Она возникает в случаях существования достаточно тесных линейных статистических связей между объясняющими переменными X1, X2, X3 ,... Xk. В результате мультиколлинеарности матрица парных коэффициентов корреляции становится слабообусловленной, близкой к вырожденной.
Точных количественных критериев для определения наличия или отсутствия мультиколлинеарности не существует. Однако существуют некоторые рекомендации по выявлению этого негативного явления, на которые следует обратить внимание. На практике о наличии мультиколлинеарности обычно судят по матрице парных коэффициентов корреляции. Если один из элементов матрицы R больше 0,8 , т.е. | rij | > 0,8 , то считают, что имеет место мультиколлинеарность и в уравнение регрессии следует включать только один из показателей Xi или Xj (как правило, тот, который имеет наибольшую связь с Y).
Прежде, чем переходить к построению регрессионной модели, необходимо проверить объясняющие переменные на наличие мультиколлинеарности. Для этого рассмотрим матрицу парных коэффициентов корреляции между факторными признаками Xi.
Матрица парных коэффициентов корреляции факторных признаков
|
Y |
х1 |
х2 |
х3 |
х4 |
х5 |
||
Y |
1 |
|
|
|
|
|
||
х1 |
-0,1051 |
1 |
|
|
|
|
||
х2 |
0,28225 |
-0,03052 |
1 |
|
|
|
||
х3 |
0,27047 |
-0,149729 |
0,22325 |
1 |
|
|
||
х4 |
-0,14131 |
0,259089 |
-0,0845 |
-0,161 |
1 |
|
||
х5 |
0,01698 |
0,14035 |
-0,0109 |
-0,07 |
-0,015 |
1 |
||
|
|
|
||||||
|
|
|
||||||
Мультиколлинеарность отсутствует. Так как все элементы матрицы меньше 0,8.
Построение регрессионной модели и её интерпретация
Необходимо использовать алгоритм пошагового регрессионного анализа с последовательным исключением незначимых регрессоров, пока все входящие в регрессионную модель факторы не будут иметь значимые коэффициенты.
Построение и оценка регрессионной модели осуществляется в Excel с помощью модуля регрессии пакета анализа данных.
В модель включены следующие факторные признаки (X1, X2, X3, X4, X5)
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вывод итогов |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Коэффи циенты |
Стандарт ная ошибка |
t-ста ти стика |
P-Зна чение |
Нижние 95% |
Верхние 95% |
Нижние 95,0% |
Верхние 95,0% |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Y |
3,254 |
7,136 |
0,456 |
0,650 |
-10,958 |
17,467 |
-10,958 |
17,467 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
X 1 |
-0,006 |
0,012 |
-0,482 |
0,631 |
-0,030 |
0,018 |
-0,030 |
0,018 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
X 2 |
0,075 |
0,036 |
2,097 |
0,039 |
0,004 |
0,147 |
0,004 |
0,147 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
X 3 |
0,018 |
0,010 |
1,811 |
0,074 |
-0,002 |
0,038 |
-0,002 |
0,038 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
X 4 |
0,251 |
0,175 |
-0,668 |
0,506 |
-0,997 |
0,496 |
-0,997 |
0,496 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
X 5 |
0,006 |
0,016 |
0,370 |
0,712 |
-0,025 |
0,037 |
-0,025 |
0,037 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В регрессионной статистике указываются множественный коэффициент корреляции (Множественный R) и детерминации (R-квадрат) между Y и массивом факторных признаков (что совпадает с полученными ранее значениями в корреляционном анализе).
Средняя часть таблицы (Дисперсионный анализ) необходима для проверки значимости уравнения регрессии.
Нижняя часть таблицы – точечные оценки bi генеральных коэффициентов регрессии βi, проверка их значимости и интервальная оценка.
Оценка вектора коэффициентов b происходит следующим образом:
Тогда оценка уравнения регрессии имеет вид:
X1
0,075
X2
0,018
X3
+ 0,251·
X4
X5
Проверку значимости регрессионных коэффициентов проводят на основе стандартной ошибки.
Наблюдаемые значения стандартной ошибки указаны в таблице результатов в столбце стандартная ошибка.
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
Y-пересечение |
3,254 |
7,136 |
0,456 |
X 1 |
-0,006 |
0,012 |
-0,482 |
X 2 |
0,075 |
0,036 |
2,097 |
X 3 |
0,018 |
0,010 |
1,811 |
X 4 |
0,251 |
0,175 |
-0,668 |
X 5 |
0,006 |
0,016 |
0,370 |
Их необходимо сравнить с коэффициентами.
Для 
наблюдаемое значение стандартной ошибки
меньше коэффициента по модулю 
,
, следовательно 
,
,
значимы.
По наблюдаемым
значениям t-статистик
указанные в таблице результатов в
столбце t-статистика
находим наименьшее по модулю 
.
Согласно алгоритму пошагового регрессионного анализа с исключением незначимых регрессоров, на следующем этапе необходимо исключить из рассмотрения переменную X5 (Среднедушевые денежные доходы рубль), имеющую наименьшую t-статистика.
II ЭТАП РЕГРЕССИОННОГО АНАЛИЗА.
В модель включены факторные признаки X1,X2 ,X3,X4 исключён X5.
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Оценка коэффициентов в случае четырех объясняющих переменных имеет вид:
Тогда оценка уравнения регрессии имеет вид:
X1
X2
X3
+ 0,259·X
4
Наблюдаемые значения стандартной ошибки указаны в таблице результатов в столбце стандартная ошибка.
|
|
|
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
Y-пересечение |
4,483 |
6,281 |
0,714 |
X 1 |
-0,005 |
0,012 |
-0,436 |
X 2 |
0,075 |
0,036 |
2,109 |
X 3 |
0,018 |
0,010 |
1,803 |
X 4 |
0,259 |
0,172 |
-0,696 |
|
|
||
Их необходимо сравнить с коэффициентами.
Для
наблюдаемое значение стандартной ошибки
меньше коэффициента по модулю 
,
,
172
следовательно,
значимы.
По
наблюдаемым значениям t-статистик
указанные в таблице результатов в
столбце t-статистика
находим наименьшее по модулю 
.Согласно
алгоритму пошагового регрессионного
анализа с исключением незначимых
регрессоров, на следующем этапе необходимо
исключить из рассмотрения переменную
X1
(Величина
прожиточного минимума на ребенка в
возрасте до 15 лет,
установленный по субъектам РФ), имеющую
наименьшую t-статистика.
III ЭТАП РЕГРЕССИОННОГО АНАЛИЗА.
ВЫВОД ИТОГОВ |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Регрессионная статистика |
|
|
|
|
|||||||||||||||||||||||||||||||||||
Множественный R |
0,364187368 |
|
|
|
|
||||||||||||||||||||||||||||||||||
R-квадрат |
0,132632439 |
|
|
|
|||||||||||||||||||||||||||||||||||
Нормированный R-квадрат |
0,099272148 |
|
|
|
|||||||||||||||||||||||||||||||||||
Стандартная ошибка |
11,59514538 |
|
|
|
|||||||||||||||||||||||||||||||||||
Наблюдения |
82 |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Дисперсионный анализ |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
df |
SS |
MS |
F |
Значимость F |
|
|
||||||||||||||||||||||||||||||||
Регрессия |
3 |
1603,591 |
534,530 |
3,976 |
0,011 |
|
|
||||||||||||||||||||||||||||||||
Остаток |
78 |
10486,897 |
134,447 |
|
|
|
|||||||||||||||||||||||||||||||||
Итого |
81 |
12090,488 |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
Коэффи циенты |
Стан дартная ошибка |
t-статис тика |
P-Значе ние |
Нижние 95% |
Верхние 95% |
Ниж ние 95,0% |
Верх ние 95,0% |
|
||||||||||||||||||||||||||||||
Y |
3,652 |
5,954 |
0,613 |
0,541 |
-8,202 |
15,507 |
-8,202 |
16 |
|
||||||||||||||||||||||||||||||
X 2 |
0,075 |
0,036 |
2,114 |
0,038 |
0,004 |
0,146 |
0,004 |
0 |
|
||||||||||||||||||||||||||||||
X 3 |
0,018 |
0,010 |
1,874 |
0,065 |
-0,001 |
0,038 |
-0,001 |
0 |
|
||||||||||||||||||||||||||||||
X 4 |
0,298 |
0,159 |
0,830 |
0,409 |
0,013 |
0,417 |
-1,013 |
0 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Оценка коэффициентов в случае трех объясняющих переменных имеет вид:
X2
X3
X4
Наблюдаемые значения стандартной ошибки указаны в таблице результатов в столбце стандартная ошибка.
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
|
Y |
3,652 |
5,954 |
0,613 |
|
X 2 |
0,075 |
0,036 |
2,114 |
|
X 3 |
0,018 |
0,010 |
1,874 |
|
X 4 |
0,298 |
0,159 |
0,830 |
|
Их необходимо сравнить с коэффициентами.
Для
наблюдаемое значение стандартной ошибки
меньше коэффициента по модулю
,
следовательно,
значимы.
Т.к. в данном случае все коэффициенты оказались значимыми, процесс исключения переменных прекращается.
Окончательная оценка регрессии со значимыми коэффициентами имеет вид:
·
X2
+ 
X3
+
X4
|
Коэффициенты |
Нижние 95% |
Верхние 95% |
Нижние 98,0% |
Верхние 98,0% |
|
Y |
3,652341 |
-8,202011 |
15,50669 |
-10,4901 |
17,79476 |
|
X 2 |
0,075168 |
0,004375 |
0,145962 |
-0,00929 |
0,159626 |
|
X 3 |
0,018374 |
-0,001141 |
0,03789 |
-0,00491 |
0,041657 |
|
X 4 |
0,29826 |
0,013292 |
0,416769 |
-1,1513 |
0,554781 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P(-8,202≤
0
≤
15,506)= 0,95
P(-10,490≤ 0 ≤17,794)= 0,98
P(0,004 ≤ 2 ≤ 0,145)= 0,95
P(-0,009 ≤ 2 ≤ 0,159)= 0,98
P(-0,001 ≤ 3 ≤ 0,037)= 0,95
P(-0,004 ≤ 3 ≤ 0,041)= 0,98
P(0,013 ≤ 4 ≤ 0,416)= 0,95
P(-1,151 ≤ 4 ≤ 0,554)= 0,98
Величина R2 характеризует долю общей дисперсии зависимой переменной, обусловленную воздействием объясняющих переменных. Множественный коэффициент детерминации r2Y/{..}) =0,781 показывает, что 78,1% доли дисперсии Y – числа разводов за год по субъектам РФ.
Коэффициент регрессии показывает среднюю величину изменения зависимой переменной Y при изменении объясняющей переменной X на единицу собственного изменения. Знак при коэффициенте указывает направление этого изменения.
Коэффициент регрессии при X2 показывает, что при росте числа семей, выселенных из жилых помещений Y в среднем увеличивается на 0,075 единиц. Построенная выше интервальная оценка показывает, что с вероятностью 0,95 при росте числа семей, выселенных из жилых помещений, риск увеличения числа разводов за год будет в пределах от 0,004 до 0,145 единиц.
Коэффициент регрессии при X3 показывает, что при росте размера ежемесячного пособия на ребенка, Y в среднем увеличивается на 0,018 единиц. Построенная выше интервальная оценка показывает, что с вероятностью 0,95 при росте размера ежемесячного пособия на ребенка, риск увеличения числа разводов будет в пределах от 0,001 до 0,037 единиц.
Коэффициент регрессии при X4 показывает, что при росте общих коэффициентов рождаемости Y в среднем увеличивается на 0,298 единиц. Построенная выше интервальная оценка показывает, что с вероятностью 0,95 при росте общих коэффициентов рождаемости, риск увеличения числа разводов будет в пределах от 0,013 до 0,416 единиц.
Сравнение исходных данных с рассчитанными по уравнению регрессии
Сравнительная таблица исходных данных показателя государственных и муниципальных образовательных учреждений (Y) с рассчитанными с помощью построенной линейной регрессионной модели
Ỹ= 3,65+ 0,75·X2 + 0,018·X3 +0,298·X4
Вывод остатков.
Регионы |
Наблюдение |
Предсказан ное Y |
Остатки |
Стандартные остатки |
Наблюдаемое Y |
Белгородская область |
1 |
4,778 |
0,222 |
0,019 |
5 |
Брянская область |
2 |
6,767 |
-2,767 |
-0,243 |
4 |
Владимирская область |
3 |
5,144 |
-2,144 |
-0,188 |
3 |
Воронежская область |
4 |
6,341 |
10,659 |
0,937 |
17 |
Ивановская область |
5 |
8,931 |
-0,931 |
-0,082 |
8 |
Калужская область |
6 |
11,571 |
-10,571 |
-0,929 |
1 |
Костромская область |
7 |
7,592 |
-4,592 |
-0,404 |
3 |
Курская область |
8 |
6,105 |
-1,105 |
-0,097 |
5 |
Липецкая область |
9 |
7,968 |
-3,968 |
-0,349 |
4 |
Московская область |
10 |
18,592 |
-5,592 |
-0,491 |
21 |
Орловская область |
11 |
6,511 |
-0,511 |
-0,045 |
6 |
Рязанская область |
12 |
8,920 |
-3,920 |
-0,345 |
5 |
Смоленская область |
13 |
6,808 |
-0,808 |
-0,071 |
6 |
Тамбовская область |
14 |
6,782 |
-2,782 |
-0,244 |
4 |
Тверская область |
15 |
12,823 |
-8,823 |
-0,775 |
4 |
Тульская область |
16 |
6,526 |
-4,526 |
-0,398 |
2 |
Ярославская область |
17 |
9,432 |
-2,432 |
-0,214 |
7 |
г.Москва |
18 |
18,238 |
82,762 |
7,274 |
101 |
Республика Карелия |
19 |
7,897 |
-4,897 |
-0,430 |
3 |
Республика Коми |
20 |
7,005 |
-3,005 |
-0,264 |
4 |
Архангельская область |
21 |
9,151 |
-7,151 |
-0,628 |
2 |
Вологодская область |
22 |
4,631 |
0,369 |
0,032 |
5 |
Калининградская область |
23 |
10,673 |
-7,673 |
-0,674 |
3 |
Ленинградская область |
24 |
11,494 |
-10,494 |
-0,922 |
1 |
Мурманская область |
25 |
10,388 |
-8,388 |
-0,737 |
2 |
Новгородская область |
26 |
9,578 |
-8,578 |
-0,754 |
1 |
Псковская область |
27 |
5,739 |
-1,739 |
-0,153 |
4 |
г.Санкт-Петербург |
28 |
20,470 |
25,530 |
2,244 |
46 |
Республика Адыгея |
29 |
9,867 |
-7,867 |
-0,691 |
2 |
Республика Калмыкия |
30 |
6,322 |
-5,322 |
-0,468 |
1 |
Краснодарский край |
31 |
3,698 |
7,302 |
0,642 |
11 |
Астраханская область |
32 |
9,089 |
-4,089 |
-0,359 |
5 |
Волгоградская область |
33 |
7,777 |
3,223 |
0,283 |
11 |
Ростовская область |
34 |
4,409 |
9,591 |
0,843 |
14 |
Республика Дагестан |
35 |
3,592 |
2,408 |
0,212 |
6 |
Республика Ингушетия |
36 |
-1,514 |
2,514 |
0,221 |
1 |
Кабардино-Балкарская Респ. |
37 |
9,106 |
-6,106 |
-0,537 |
3 |
Карачаево-Черкесская Респ. |
38 |
4,813 |
-2,813 |
-0,247 |
2 |
Респ. Северная Осетия - Алания |
39 |
6,815 |
-0,815 |
-0,072 |
6 |
Чеченская Республика |
40 |
3,742 |
-0,742 |
-0,065 |
3 |
Ставропольский край |
41 |
11,573 |
-5,573 |
-0,490 |
6 |
Республика Башкортостан |
42 |
4,878 |
5,122 |
0,450 |
10 |
Республика Марий Эл |
43 |
11,099 |
-9,099 |
-0,800 |
2 |
Республика Мордовия |
44 |
3,831 |
-1,831 |
-0,161 |
2 |
Республика Татарстан |
45 |
4,732 |
13,268 |
1,166 |
18 |
Удмуртская Республика |
46 |
5,773 |
-0,773 |
-0,068 |
5 |
Чувашская Республика |
47 |
5,324 |
-1,324 |
-0,116 |
4 |
Пермский край |
48 |
2,910 |
7,090 |
0,623 |
10 |
Кировская область |
49 |
10,633 |
-6,633 |
-0,583 |
4 |
Нижегородская область |
50 |
4,125 |
8,875 |
0,780 |
13 |
Оренбургская область |
51 |
8,654 |
-2,654 |
-0,233 |
6 |
Пензенская область |
52 |
6,612 |
-1,612 |
-0,142 |
5 |
Самарская область |
53 |
4,651 |
12,349 |
1,085 |
17 |
Саратовская область |
54 |
10,792 |
-3,792 |
-0,333 |
7 |
Ульяновская область |
55 |
12,202 |
-7,202 |
-0,633 |
5 |
Курганская область |
56 |
10,672 |
-7,672 |
-0,674 |
3 |
Свердловская область |
57 |
5,177 |
12,823 |
1,127 |
18 |
Тюменская область |
58 |
3,317 |
10,683 |
0,939 |
14 |
Ханты-Мансийский авт. округ-Югра |
59 |
10,549 |
-5,549 |
-0,488 |
5 |
Ямало-Ненецкий авт. округ |
60 |
2,733 |
-1,733 |
-0,152 |
1 |
Челябинская область |
61 |
9,238 |
3,762 |
0,331 |
13 |
Республика Алтай |
62 |
1,001 |
-0,001 |
0,000 |
1 |
Республика Бурятия |
63 |
8,232 |
-4,232 |
-0,372 |
4 |
Республика Тыва |
64 |
-0,800 |
1,800 |
0,158 |
1 |
Республика Хакасия |
65 |
4,781 |
-3,781 |
-0,332 |
1 |
Алтайский край |
66 |
27,887 |
-19,887 |
-1,748 |
8 |
Забайкальский край |
67 |
8,641 |
-5,641 |
-0,496 |
3 |
Красноярский край |
68 |
8,175 |
1,825 |
0,160 |
10 |
Иркутская область |
69 |
14,739 |
-3,739 |
-0,329 |
11 |
Кемеровская область |
70 |
4,714 |
6,286 |
0,552 |
11 |
Новосибирская область |
71 |
10,046 |
4,954 |
0,435 |
15 |
Омская область |
72 |
3,735 |
6,265 |
0,551 |
10 |
Томская область |
73 |
3,315 |
3,685 |
0,324 |
7 |
Республика Саха (Якутия) |
74 |
3,256 |
1,744 |
0,153 |
5 |
Камчатский край |
75 |
4,272 |
-2,272 |
-0,200 |
2 |
Приморский край |
76 |
7,062 |
-0,062 |
-0,005 |
7 |
Хабаровский край |
77 |
5,618 |
4,382 |
0,385 |
10 |
Амурская область |
78 |
4,926 |
-0,926 |
-0,081 |
4 |
Магаданская область |
79 |
4,196 |
-3,196 |
-0,281 |
1 |
Сахалинская область |
80 |
7,449 |
-6,449 |
-0,567 |
1 |
Еврейская автономная область |
81 |
3,882 |
-2,882 |
-0,253 |
1 |
Чукотский автономный округ |
82 |
6,829 |
-5,829 |
-0,512 |
1 |
Проанализировав графу Стандартные остатки можно прийти к выводу, что регионы № 4 (Воронежская область), 10 (Московская область), 18 (г. Москва), 28 (г.Санкт-Петербург), 45 (Республика Татарстан), 57 (Свердловская область) демонстрируют большее число разводов в год по всем рассматриваемым регионам. А для региона № 66 (Алтайский край) характерна обратная ситуация - отрицательное отклонение от линии регрессии.
Рис.5 Диаграмма сравнения исходных данных показателя (Y) с рассчитанными с помощью линейной регрессионной модели