1)Мета і задачі дисципліни

«Математична обробка геодезичних вимірів»

Предмет і задачі курсу МОГВ. Подія. Види подій. Повна група подій. Відносна частота та ймовірність подій. Додавання та множення ймовірностей. Залежні та незалежні події. Формула повної ймовірності. Випадкова величина. Ряд розподілу. Многокутник розподілу. Функція розподілу. Функція щільності розподілу. Ймовірність попадання випадкової величини в заданий інтервал. Числові характеристики розподілу випадкової величини. Характеристики положення. Характеристики розсіювання. Нормальний закон розподілу та його параметри. Моменти нормального закону розподілу. Ймовірність попадання нормально розподіленої величини в заданий інтервал. Нормальна функція розподілу. Ймовірне відхилення. Поняття системи випадкових величин. Функція розподілу та функція щільності розподілу системи двох величин. Числові характеристики системи. Оцінки характеристик системи двох величин. Кореляційний момент та коефіцієнт кореляції і рівняння регресії. Закон великих чисел. Теорема Чебишева. Центральна гранична теорема Ляпунова. Завдання математичної статистики. Проста статистична сукупність. Статистична функція розподілу. Статистичний ряд розподілу. Гістограма. Числові характеристики статистичного розподілу. Вирівнювання статистичних рядів. Критерії перевірки узгодженості. Особливості обробки. Оцінки для математичного сподівання та дисперсії. Довірчий інтервал. Довірча ймовірність. Точні та наближені методи побудови довірчих інтервалів. Предмет і завдання теорії помилок. Відомості про вимірювання та їх помилки. Класифікація помилок вимірювань. Критерії точності результатів вимірювань. Абсолютні та відносні помилки. Найбільш надійне значення рівноточно виміряної величини. Оцінки точності найбільш ймовірного значення. Помилка простої арифметичної середини. Помилка результатів вимірювань. Формула Бесселя.

Довірчий інтервал для істинного значення величини. Найбільш надійне значення нерівноточно виміряної величини. Ваги вимірювань. Ваги функцій виміряних величин. Помилка одиниці ваги. Формула Бесселя. Формула Ферреро. Помилки найбільш надійного значення та результатів вимірювань. Довірчий інтервал для істинного значення величин. Подвійні вимірювання і завдання їх математичної обробки. Оцінка точності подвійних рівноточних вимірювань. Оцінка точності подвійних нерівноточних вимірювань. Принцип найменших квадратів і його зв’язок з принципом арифметичної середини. Способи розв’язування і завдання зрівноважування. Загальна теорія способу. Види параметричних рівнянь поправок. Послідовність зрівноважування.

Матрична форма запису основних рівнянь. Обчислення коефіцієнтів нормальних рівнянь. Контроль обчислення коефіцієнтів нормальних рівнянь. Способи розв’язування системи нормальних рівнянь

Розв’язування системи нормальних рівнянь за способом Гауса. Способи контролю розв’язування системи. Повна та скорочена схема розв’язування системи алгоритмом Гауса. Оцінка точності вирівняних невідомих (параметрів). Визначення вагових коефіцієнтів (спосіб додаткових граф, Ганзена і Енке). Оцінка точності функцій вирівняних невідомих. Обчислення ваг функцій в додатковій графі. Заключні обчислення.Оцінка точності. Загальна теорія корелатного способу. Види умовних рівнянь. Послідовність зрівноважування. Розв’язування системи нормальних рівнянь Матрична форма запису основних рівнянь. Обчислення коефіцієнтів нормальних рівнянь. Контроль обчислення коефіцієнтів нормальних рівнянь. Оцінка точності функцій виміряних величин. Обчислення оберненої ваги функції в додатковій графі. Заключні обчислення.Оцінка точності. 2) Події, види подій

Події - здійснення кожного окремого спостереження , досліда або наміру називається випробуванням, називається подією.

Подія яка при повторюванні досліда може наступити а може не наступати називається випадковою подією Види подій

1. Проста випадкова подія- це такий результат випробувань який повністю описується однією подією 2.Складна випадкова подія - це подія , що складається з двох чи більше простих подій 3. Достовірною - називається подія яка обовязково відбудеться при реалізації комплексу умов 4. Неможлива - подія яка нівякому разі не відбудеться при певному комплексу подій 5. Випадковою називається подія - яка при реалізації в певному комплексу умов яка відбудеться або не відбудеться. 3) Імовірність подій

1.2. Імовірність події. Класична i статистична ймовірності та їх обчислення

Поняття ймовірності події виникло як інтуїтивне поняття, яке дає кількісну оцінку можливості появи події A i позначається Р(А).

Класичне й статистичне означення ймовірності.

Розглянемо простір (множину) елементарних подій А1, А2, ... Аn при виконанні комплексу умов S.

, (1)

де m кількість елементарних подій, сприятливих А,

n кількість вcix можливих елементарних подій.

За класичним означенням ймовірність появи події шукають не проводячи ніяких дослідів, виходячи з теоретичних міркувань. На практиці часто доводиться мати справу iз статистичною ймовірністю. Її часто називають відносною частотою появи події i позначають

Р = ,

де m кількість випробувань, в яких подія А з'явилась,

n загальна кількість випробувань.

В дослідах статистична ймовірність коливається в околі деякого постійного числа, змінюючись мало, причому тим менше, чим більше проведено дослідів. Ця стала отримала назву класичної ймовірнocтi. Для існування статистичної iмовірнocтi необхідно:

1) мати можливість провести необхідну кількість випробувань, в кожному з яких подія А настане або нi;

2) наявність стійкості відносних частот появи події А в різних серіях достатньо великого числа випробувань.

Статистична ймовірність (the statistical probability) має властивості:

1) Р(А)0 це очевидно, оскільки m0;

2) для вірогідної події ;

3) якщо події А і В несумісні, то статистична імовірність події С=А+В дорівнює сумі статистичних ймовірностей Р(А+В)=Р(А)+Р(В).

Легко бачити, що формулою (1) можна користуватись лише у випадку скінченних m i n. Якщо m і n нескінченні, то класична імовірність вводиться аксіоматично. Класичною імовірністю Р(А) події А, яка визначається простором елементарних подій , називається числова функція, яка задовольняє такі умови:

1) Р(А);

2) ;

3) для несумісних подій А і В: Р(А+В)=Р(А)+Р(В).

Умови 1) - 3) отримали назву аксіом теорії ймовірностей. Аксіоматичне означення класичної ймовірності зручне в теорії, проте воно не дає способу її обчислення. Такий спосіб дає визначення класичної ймовірності як границі статистичної. Якщо проводяться серії однотипних дослідів, в кожній з яких обчислені статистичні ймовірності, то отримаємо послідовність {Р1*(А), Р2*(А), ... Рn*(А)}, границя якої і визначає класичну ймовірність при .

Введення класичного означення ймовірності відбулося не в результаті однократної дії, а зайняло певний проміжок часу, як і формування самої теорії ймовірностей. Тобто відбувалося безперервне вдосконалення формування, перехід від конкретних задач до загального випадку.

4)Множення імовірності. Теорема множення

Добутком двох подій А і В називається подія С, що полягає у здійсненні під час одиничного випробовування й події А, і події В.

Подія А називається від події В, якщо ймовірність події А не залежить від того, відбулась чи ні подія В.

Дві події А та В називають залежними, якщо ймовірність настання однієї з них залежить від того, настала друга подія чи ні.

Умовною ймовірністю РА(В) події В називається ймовірність події В, знайдена в припущенні, що подія А вже настала.

З означення назалежних подій випливає, що настання однієї з них не змінює ймовірності настання другої. Тому для незалежних подій справджуються рівності:

P_A(B) = P(B) P_B(A)=P(A)

Отже, умовні ймовірності незалежних подій дорівнюють їх безумовним імовірностям.

Теорема 1. Імовірність добутку двох залежних подій А і В дорівнює добутку ймовірності однієї з них на умовну ймовірність другої, яка знайдена з припущенням того, що перша подія настала, тобто

Формула множення ймовірностей P(AB) = D(A)P_A(B)

Доведення. Нехай з усієї кількості n елементарних подій k сприяють події А і нехай з цих подій l сприяють події В, а, отже і події АВ. Тоді:

P(AB)=1/n=k/n *1/k=P(A)P_A(B)

що й треба було довести.

Теорема 2. Імовірність добутку двох незалежних подій А і В дорівнює добутку імовірностей цих подій, тобто

P(AB)+P(A) * P(B)

Доведення. Якщо А і В - незалежні події, то

P_A(B)=P(B)

і формула: P(AB)+P(A)P_A(B) перетворюється у формулу P(AB)=P(A)*P(B)

5.Закони розподілу випадкових величин

Закони розподілу випадкових величин називається співвідношення, яке встановлює зв’язок між окремими двома величинами та відповідає ймовірностям

Функцію розподілу ведичини Х , яку приймають F(x), називають ймовірність того, що наукова величина Х при випробовуванні набуде значення менше Х.

6.Основні характеристики вип. Величини: математичне очікування, дисперсія, мода, медіана.

Математичне очікування – сума добутків перервних випадкових величин на їх ймовірність

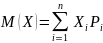
Дисперсія –математичне очікування квадрата відхилення випадкової величини від її математичного очікування.

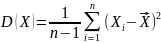
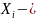результат одного спостереження випадкової величини

- оцінка

Мода - значення випадкової величини, що трапляється найчастіше в сукупності спостережень.

Медіана - це величина, що знаходиться в середині ряду величин, розташованих у зростаючому або спадному порядку.

7)Види випадкових подій

Дві події А і В називаються несумісними (incompatible), якщо поява однієї із них виключає появу іншої в даному досліді, в іншому разі події сумісні (compatible).

Дві події А і В називаються рівноможливими, якщо при виконанні комплексу умов S однаково можливі появи подій А і В.

8.Додавання ймовірностей. Теорема додавання

Сумою кількох простих подій називається складну подію, яка виражається в появі однієї із цих простих подій, немає значення якої.

Нехай задані несумісні події

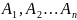
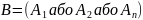
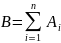
Теорема додавання

Ймовірність суми попарно несумісних подій дорівнює сумі ймовірності цих подій.

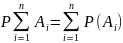
9.Випадкові величини. Дискретні та неперервні випадкові величини

Випадкові величини. Випадковою величиною називається величина, яка при одному випробуванні може припинити те чи інше своє можливе значення.

Дискретні та неперервні випадкові величини. Дискретним називають випадкову величину, яка може приймати окремі ізольовані значення з певними ймовірностями. Неперервною називається величина, яка при випробуванні може приймати будь – яке одне можливе значення які неперервно заповнюють їх інтервал.

10. Функія розподілу випидкових величин

Випадкова величина - це величина, яка в результаті випробувань може приймати певні значення (із сукупності своїх значень) з певною ймовірністю. Випадковою можна назвати будь-яку (не обов'язково чисельну) змінну x, значення якої х створюють множину випадкових елементарних подій {х}.

Розрізняють дискретну і неперервну випадкові величини.

Дискретною випадковою величиною називається випадкова величина, що приймає скінчене число значень з множини, елементи якої можна пронумерувати. Неперервною випадковою величиною називається випадкова величина, можливі значення якої неперервно заповнюють деякий інтервал.

Рядок розподілу дискретної випадкової величини x може бути представлений як у табличній формі - у вигляді таблиці, де перераховано значення випадкової величини х1, х2, хп з відповідними до них ймовірностямир1, р2, рп (див. табл. 3.2), так і у вигляді графічного зображення (рис. 3.7).

11.Статистичні зв*язки.Коефіцієнт кореляції.Рівняння регресії.

Статистична залежність ,коли умовне математичне сподівання однієї випадкової величини є функцією

значень, які приймає інша

Коефіцієнт кореляції

Рівняння регресії

Аналогічно можна побудувати лінію кореляції або регресії А 'на Y

12.Нормальний закон розподілу

Випадкова величина ξ нормально розподілена або підпорядковується закону розподілу Гаусса, якщо її щільність розподілу має вигляд:

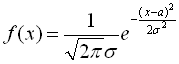, де а ‑ довільне дійсне число,   > 0.

13.Перевірка відповідності фактичних розподілів теоретичним законом

Однією з найважливіших задач математичної статистики є встановлення теоретичного закону розподілу випадкової величини, що характеризує ознаку, що вивчається за дослідним (емпіричним) розподілом, що являє собою статистичний ряд.

Для розв’язання такої задачі необхідно визначити вид та параметри закону розподілу.

Пропозиція щодо закону розподілу може бути висунута з теоретичних посилань, досвіду аналогічних випробувань або графічного зображення емпіричного закону розподілу.

Параметри розподілу, як правило, невідомі, тому їх заміняють найкращими оцінками за вибіркою.

Якщо відомий закон розподілу U, то можна знайти ймовірність того, що U прийняла значення не менше ніж, фактично спостерігаєме у досліді u, тобто U≥u. Якщо P(U≥u)=α мала, то це позначає у відповідності до принципу практичної впевненості, що такі, як у досліді, та більші відхилення практично неможливі. В цьому випадку нульову гіпотезу відкидають. Якщо ж ймовірність P(U≥u)=α не мала, то гіпотезі Н₀ можна вважати такою, що не містить протиріч до вибіркових даних.

Χ² – критерій Пірсона. На практиці частіше за всього використовують Χ² – критерій Пірсона у ньому у якості міри розходження U береться величина Χ², що дорівнює сумі квадратів відхилень частостей (статистичних ймовірностей) w_i від гіпотетичних р_і, що розраховані за розподілом, що передбачається, та взяті з деякими вагами с_і.

14-Предметні задачі теорії вимірювань

1) встановлення законів розподілу похибок вимірювань;

2) визначення на основі результатів вимірювань найбільш надійних значень

шуканих величин;

3) виконання оцінки точності отриманих значень шуканих величин;

4) визначення допусків, тобто граничних значень похибок;

5) встановлення законів накопичення похибок як у процесі вимірювань, так і

при опрацюванні їх.

15.Вимірювання та їх класифікація

Вимірювання - це встановлення відношення величини, що вимірюється, до

іншої однорідної величини, яку прийнято за одиницю міри, тобто > Розді л IV

вимірювана величина; N - одиниця міри; L - числове значення величини М.

мірювання поділяють на:

1.Прямі (безпосередні) та непрямі (посередні) за фізичним виконанням

. Якщо вимірювану величину можна безпосередньо порівняти з

міри, то це є пряме вимірювання. Довжина лінії, виміряна за допомогою

овальної стрічки, величина кута, який виміряно за допомогою теодоліта,

виміряного за допомогою нівеліра та рейки - це є прямі

2. Рівноточні та нерівноточні за точністю, яка обумовлюється умовами

звань. Рівноточні вимірювання однієї або декількох однорідних величин -

результати вимірювань, які отримано при однакових умовах, а саме одним

ке методом, спостерігачами однакової кваліфікації, приладами однакової

;ті вимірювання, при однакових приблизно зовнішніх умовах тощо.

3.. Необхідні та додаткові за кількістю. Вимірювання, які проведено для

отримання хоча б однієї системи значень шуканих величин, називаються

необхідними. Якщо з тією ж метою крім необхідних вимірювань виконані ще

якісь вимірювання, то вони називаються додатковими або надлишковими.

4). Залежні та незалежні за умовами вимірювань. Залежними називаються ч а к і

вимірювання якоїсь величини, які впливають на результат вимірювання іншої

величини. У протилежному випадку вимірювання називаються незалежними.

16.Похибки вимірювань і поправки до їх результату

У процесі вимірювання крім об'єкта вимірювання, приймають участь прилади,спостерігачі, які використовують ці прилади, а також і, звичайно, на результат впливає зовнішнє середовище. Весь цей комплекс умов може змінюватись і розрізнювати точно ці зміни неможливо. Тому в результаті вимірювання отримані рівняння будуть відрізнятися від істинних . Розглянемо істинне значення L вимірюваної величини та її виміряні значення (і = 1, п). Тоді величини A=l- L

17.Класифікація похибок вимірювань

1) при даних умовах вимірювань випадкові похибки за абсолютною величиною залишаються завжди меншими за якесь граничне значення;

2) частота малих за абсолютною величиною похибок є більшою за частоту великих;

3) частоти додатних і від'ємних похибок є завжди однаковими;

4) границя середнього арифметичного значення випадкових похибок є рівною нулеві при необмеженому зростанні їх кількості;

5) у ряді випадкових похибок при переході від однієї похибки до іншої не проявляється ніякої закономірності щодо її абсолютної величини.

18.Критерії для оцінки точності результатів вимірювань

Середня квадратична похибка є найкращим критерієм для оцінки точності

вимірювань. Вона має такі переваги над середньою та ймовірною похибками:

1). Середня квадратична похибка є досить чутливою мірою точності тому,

що на її величину сильніше впливають великі за абсолютною величиною випадкові

похибки, що в основному і визначають надійність результатів вимірювань.

2). Середня квадратична похибка вже при деякій відносно не дуже великі

кількості вимірювань набуває сталого значення і в подальшому при збільшенні

кількості вимірювань змінюється дуже повільно.

3). За величиною середньої квадратичної похибки можна знайти граничну

похибку, тобто таке найбільше за абсолютною величиною значення випадкової

похибки, яке ще може з'явитися при даних умовах вимірювань. Потрійна середня

квадратична похибка приймається за граничну.

4). Знаючи середні квадратичні похибки якихось величин, можна легко визначити

середні квадратичні похибки інших величин, функціонально пов'язаних із ними.

Розрізняють абсолютні та відносні похибки. Істинну похибку А, середню 0,

ймовірну а середню квадратичну т називають абсолютними похибками.

Часто при вимірюванні лінійних величин та площ використовують відносні

похибки. Це безрозмірні величини, які обчислюються відношенням абсолютних

похибок до виміряного значення якоїсь величини. Розглянемо виміряне значення .v

довільної величини.

19. Розподіл ймовірностей випадкових похибок

Конференціальна функція даного розподілу, або функція густини має вигляд

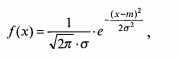
Функція нормального розподілу істинних випадкових похибок А

гакою:

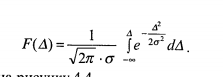
20. Дослідження похибок на випадковість

Для цього потрібно:

1) побудувати інтервальний статистичний ряд розподілу похибок вимірювань

відповідний йому дискретний статистичний ряд;

2) за даними побудованих рядів обчислити оцінки параметрів нормального

поділу, а саме середнє вибіркове та вибіркову дисперсію;

3) знайти всі значення функції густини нормального розподілу за даними

кретного статистичного ряду і на їх основі побудувати криву розподілу та

ограму відносних частот на одному графіку;

4) із використанням критерію Пірсона перевірити справедливість

зформульованої нульової гіпотези , якщо альтернативною гіпотезою , буде

заперечення нульової гіпотези, тобто досліджуваний ряд похибок

не підлягає нормальному закону розподілу.