21. Скп незалежно виміряних величин?

Середня квадратична похибка функцій виміряних величин

Дуже часто виникає необхідність визначення середньої квадратичної похибки величин, не безпосередньо виміряних, а отриманих шляхом обчислень із інших виміряних величин. Тобто шукана величина визначається шляхом обчислень функції виміряних величин. Похибка функції залежить від похибок аргументів, що входять до неї. Припустимо що у функції загального виду:

. (1.2.13)

аргументи незалежно виміряні із

середньою квадратичною похибкою . Якщо

X, Y, … U – істинні значення (точні) аргументів, то їхні істинні похибки дорівнюють :

Δx = x – X

15

Δy = y – Y

…………..

Δu = u – U,

Розклавши другий доданок у ряд Тейлора з урахуванням перших двох членів ряду знаходимо :

 f				f		 f		
F  f (x, y,...u)  f (x, y,...u)  		x  			y ... 			u  R
	x			y			u	
								

,

де R – залишковий член розкладання, дорівнює сумі всіх нелінійних членів ряду Тейлора, його значенням у геодезії в більшості випадків можна знехтувати.

Піднесемо ліву та праву частини до квадрата, підсумувавши та розділивши на (n) з врахуванням формули

Гаусса , отримуємо :

			f2
m2				
				
F
			x 
				

			f2
m2				
				
x
			y 
				

			f2
m2	...			
				
y
			u 
				

									1
m2		f 		f 
	 2					(x y	x y	...x y )		...
u						1 1	2 2	n n n
		x 		y 
					

Згідно із формулою визначення коефіцієнта кореляції :

16

n

_

_



( x  x)( y

 y)

r 

i 

1

i

i

,

nmxm y

де

=

;

;

;

.

Запишемо

n

_

_

n

.

(x x)( y

 y) 

x

y  rnm

m

i

i

i

x

y

i1

i1

Для попарно корельованих аргументів знаходимо :

m 



f 

2



f 

2



f 

2



f 

f 

m



f 

f 

(1.2.14)





mx2





my2

... 



mu2

 2



r m

x

... 2



r m m

F

 x 







u 







xy

y







xu x u



y 

x 

y 

x 

y 

Значення часткових похідних зазвичай визначають за приблизними значеннями аргументів. При обчисленнях за даною формулою похідні обчислюються зі збереженням трьох значущих цифр, у кінцевому результаті отримують дві значущі

цифри. Коефіцієнти кореляції попередньо визначають із спеціальних досліджень.

Якщо аргументи функції 1.2.13 некорельовані ( =0), то замість 1.2.14 отримуємо формулу :

		f		2
mu 			
		x1	
			

			f			2
2
					
mx			x		
1				2
					

2		f
mx	
	... 	xn
2	

	2					2
	2	n		f		2 .		(1.2.15)
					
	mn 					mxi
					
		i1		xi 

Квадрат середньої квадратичної похибки функції загального виду дорівнює сумі добутку квадратів похідних від функції по кожному аргументу на квадрати середніх квадратичних похибок відповідних аргументів.

Приклад : у трикутнику виміряно дві сторони і кут між ними; а = 30 м ± 0,10 м, b = 40 м ± 0,15 м; α = 45⁰ ± 10´.

Визначити відносну середню квадратичну похибку площі трикутника.

Розв’язування: .

17

Знайдемо похідні від цієї функції за аргументами a, b і α. Отримаємо:

p  1 bsin  ;

p  1 a sin  ;

p

 1 a cos .



a 2

b

2

2

Потім, згідно з 1.2.15, отримаємо :

m2  

1

b2 sin 2

m2

1

a2 sin 2 m2

1

a2b2

cos2 

m2







2

4

a

4

b

4



Примітка:

якщо mα

надано в секундах або мінутах,

то

завжди m_α ділимо на ρ

Підставивши в цей вираз числові значення відповідних величин отримаємо:

та

Лінійні функції

Д ана функція виду ,

(*)

де якій , , … - постійні числа, а , … - незалежні аргументи виміряні з середніми квадратичними похибками , , … .

Необхідно визначити середню квадратичну похибку ( ) функції (u).

	f	
			 ki , a
Для лінійної функції (*) часткові похідні 	x1	
		
.

Квадрат середньоквадратичної похибки функції (u) дорівнює сумі добутку сталих на квадрат середньої квадратичної похибки відповідних аргументів.

18

Для функції часткові похідні

	f	
			 1. Тоді:
	x1	
		

.

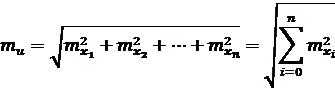Квадрат середньої квадратичної похибки алгебраїчної суми будь-якої кількості аргументів, отриманих із незалежних вимірювань, дорівнює сумі середніх квадратичних похибок

доданків.	В	окремому	випадку	при	=
		, тобто коли всі аргументи виміряні з

однаковою точністю,

.

Для функції u = kx множення виміряної величини на постійний множник

k – безпомилкове постійне число;

х – аргумент, отриманий із вимірювань.

.

Середня квадратична похибка добутку постійного (k) на аргумент (х), отриманий із вимірювань, дорівнює добутку постійного на середню квадратичну похибку вимірювання аргументу.

Якщо функція має вигляд

,

то спочатку необхідно зробити її логарифмування

ln u = ln x₁ + ln x₂ +...+ ln x_n – ln y₁ – ln y₂ – ... – ln y_n.

19

Використовуючи формулу 1.2.15 отримаємо

u



1

,

xi

xi

u



1

та

yi

yi

=

n

 m



2

n

 myi 

2



xi











 .

(1.2.16)



xi







i1





i1

 yi



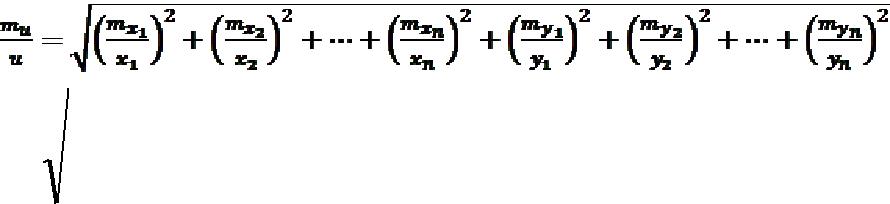
У деяких випадках оцінюють не самі величини, а десятинні логарифми цих величин. Для визначення зв’язку між середньоквадратичною похибкою величини та середньоквадратичною похибкою десятинного логарифма цієї ж величини використовуємо зв’язок між десятинними та

натуральними логарифмами								lgu = M lnu, тоді :
			 mu 
mlg u			 M 				,	(1.2.17)
			 u				
		 u			
	mu				mlgu .				(1.2.18)
		 M			
		Значення mlgu зазвичай визначають в одиницях шостого

знака логарифма, тому помноживши ліву та праву частину формули 2.17 на 10⁶, отримаємо :

						;
mu 		u			mlg u ,
	106
			M
звідки, враховуючи М ≈ 0,434,
				.		(1.2.19)
Приклад:				визначити відносну середню		квадратичну

п охибку сторони , якщо середня квадратична похибка

20

логарифма цієї сторони = 3,7 одиниці шостого знака логарифма.

Рішення: підставляємо в 1.2.19 замість значення = 3,7 знаходимо :

.

При виконанні різних розрахунків часто виникає необхідність за відомою точністю функції знайти точність визначення кожного аргументу. При розв’язуванні цієї задачі зазвичай використовують принцип рівного впливу, згідно якому вважають



f



2



f





f



2





m2



m2

 ... 



m2



x1



x1



x2



x2





n











xn 

Тоді замість виразу 1.2.15 отримаємо

	f 	2
		2
		mx .
	x 



f 

2

2

f

mu





mx

n ,

n

mx

x



x 

звідки

f

m

f

m

f

m

u







m

.

(1.2.20)

x

x

n

x1

x2

2

xn

1

n

Приклад: перевищення між точками отримано методом тригонометричного нівелювання за формулою h = S tgν.

З якою точністю необхідно визначити горизонтальне прокладення S = 145,00м і кут нахилу ν = 4⁰30’, щоб перевищення h було отримано з середньою квадратичною

похибкою = 0,05 м.

Розв’язування: за формулою 1.2.15 знаходимо

.

21

Згідно з 2.20 :

;
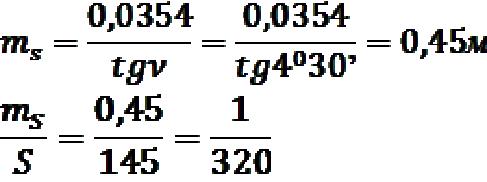