Тема 3. Ряды динамики

При изучении данной темы необходимо усвоить: понятие ряда динамики и их виды, основные правила их построения и использования для анализа динамики процессов, условия сопоставимости уровней рядов динамики, способы преобразования рядов динамики, понятие тренда.

Ряд динамики (временной ряд) представляет собой ряд, рacположенных в хронологической последовательности числовых значений статистического показателя, характеризующего изменение изучаемого явления во времени.

В каждом ряду динамики имеются два основных элемента: 1) показатель времени t;

2) уровень ряда у_t

Показателями времени могут быть периоды (год, квартал, месяц, сутки) и моменты (определенная дата на начало или конец периода). Соответственно и ряды разделяются на интервальные и моментные.

Уровень ряда - это размер (объем, величина) того или иного явления (показателя), достигнутый за определенный период времени или к определенному моменту.

Под трендом понимают плавное изменение, определяющее общее направление развития, основную тенденцию ряда динамики. Это систематическая составляющая, характеризующая долговременное воздействие факторов на динамику изучаемого показателя.

Выявление тренда в статистике называют также выравниванием ряда динамики, а методы выявления основной тенденции – методами выравнивания. Выравнивание можно осуществлять разными способами: методом укрупнения интервалов, сглаживанием методом скользящей средней или аналитическим выравниванием.

Метод скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по счету уровней, затем из такого же числа уровней, но начиная со второго по счету далее - начиная с третьего и т. д. Таким образом, средняя как бы «скользит» по ряду динамики, передвигаясь на один уровень. Например,

, , , и.т.д.

Абсолютные, относительные и средние показатели рядов динамики.

Для количественной оценки динамики правовых явлений применяются такие статистические показатели как абсолютные приросты, темпы роста, темпы прироста, которые делятся на базисные, цепные и средние. В основе расчета этих показателей динамики лежит сравнение уровней ряда динамики. Если сравнение осуществляется с одним и тем же уровнем, принятым за базу сравнения, то эти показатели называются базисными. В качестве базисного выбирается либо начальный уровень в ряду динамики, либо уровень с которого начинается какой-то новый этап развития явления. Если сравнение осуществляется при переменной базе и каждый последующий уровень ряда сравнивается с предыдущим, то вычисленные таким образом показатели динамики называются цепными.

Абсолютный прирост (Δу) равен разности двух сравниваемых уровней.

Базисный абсолютный прирост

Δy_t^б=y_t-y_б.

Цепной абсолютный прирост

Δy_t=y_t-y_t-1.

Средний абсолютный прирост

где y_t - уровень сравниваемого периода;

y_t-1 - уровень предшествующего периода;

y_б - уровень базисного периода;

y₁,y_n – первый и последний уровни ряда соответственно;

n - число уровней ряда.

Темп роста (Т ) - это отношение уровня ряда одного периода к уровню ряда другого периода, выраженное в процентах.

Базисный темп роста T_t^б=

Цепной темп роста T_t=

Средний темп роста

_{Замечание. Если темп роста и средний темп роста вычисляются в долях (не умножаются на 100%), то они называются соответственно коэффициентом роста и средним коэффициентом роста.}

Темп прироста (Т_пр)вычисляется как отношение абсолютного прироста (Δу) к уровню, принятому за базу сравнения. Темп прироста показывает, на сколько процентов изменился сравниваемый уровень по отношению к уровню, принятому за базу сравнения. Он может быть положительным, отрицательным или равным нулю.

Базисный темп прироста Т_{пр t}^б=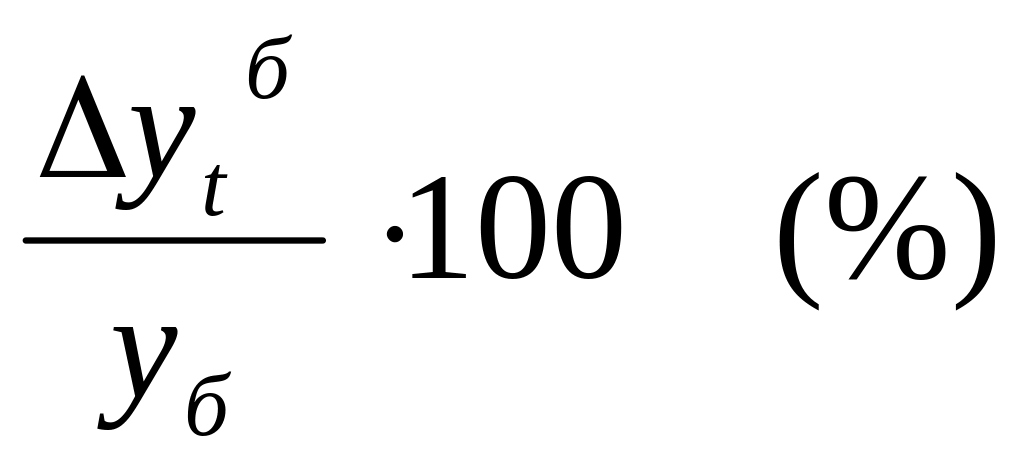

Цепной темп прироста Т_{пр t}=

Средний темп прироста

_{Замечание. Если вычислен соответствующий темп роста, то темп прироста равен:}

_{Тпр.=Тр.-100 (%).}