12. Сопротивление соединения проводников. Температурная зависимость сопротивления для металлов и полупроводников:

Последовательное соединение проводников: I₁ = I₂ = … = I_n = I

; ;

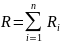Параллельное соединение проводников: U₁ = U₂ = … = U_n = U

;

Температурная зависимость сопротивления:

А) для металлов: ρ=ρ₀*(1+αt) или R=R₀*(1+αt), где ρ и ρ₀, R и R₀ – удельные сопротивления и сопротивления проводника при температурах t и 0⁰С (шкала Цельсия), α – температурный коэффициент сопротивления. У некоторых металлов при температуре, близкой к абсолютному нулю, сопротивление скачком уменьшается до нуля (явление сверхпроводимости).

B) для полупроводников: величина электропроводимости зависит от концентрации носителей заряда и их подвижности. Для полупроводников существуют такие пределы концентрации зарядов и их подвижности, что обуславливает изменение электропроводности на 13-14 порядков выше, чем у проводников. Сопротивление полупроводников с ростом температуры резко уменьшается по экспоненциальному закону – , где R(T) – сопротивление полупроводника при температуре T, B – коэффициент, характеризующий зависимость подвижности заряда от температуры, ∆W – энергия активизации полупроводника, k – постоянная Больцмана.

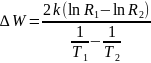
13. Закон Ома в интегральной и дифференциальной формах:

Закон Ома для неоднородного участка цепи в интегральной форме, который является обобщенным законом Ома: I = (φ₁ – φ₂ + ε₁₂)/R.

Частные случаи:

1) Если на данном участке цепи источник тока отсутствует (нет сторонних сил), то получаем закон Ома для однородного участка цепи: I = U/R;

2) Если цепь замкнута (∆φ = 0), то получаем закон Ома для замкнутой цепи: I = ε/(R+r), ε – ЭДС, R и r – внешнее и внутреннее сопротивления;

3) Если цепь разомкнута, то I = 0 и ε₁₂ = φ₁ – φ₂, т.е. ЭДС в разомкнутой цепи равна разности потенциалов на ее концах.

4) В случае короткого замыкания сопротивление внешней цепи R = 0: I = ε/r.

Закон Ома в дифференциальной форме: j = γ*E, где γ – удельная электропроводность ([γ] = 1[См/м] – Сименс на метр), E – напряженность. Этот закон связывает плотность тока с напряженностью.

14. Правило Кирхгофа:

Любая точка разветвления цепи, в которой сходится не менее трех проводников с током, называется узлом. Ток, входящий в узел, считается положительным, а ток, выходящий из узла, — отрицательным.

I правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю:

Например, для узла A первое правило Кирхгофа запишется так: I₁-I₂-I₃+I₄+I₅-I₆ = 0

II правило Кирхгофа: В любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил тока I_i на сопротивление R_i соответствующих участков этого контура равна алгебраической сумме ЭДС ε_k, встречающихся в этом контуре:

Например, для обхода по часовой стрелке замкнутого контура ABCDA 2 правило Кирхгофа имеет вид: I₁R₁-I₂R₂+I₃R₃+I₄R₄ = ε₁ – ε₂ + ε₃

15. Работа и мощность тока. Закон Ома для неоднородного участка цепи:

Работа по перемещению заряда между 2-мя точками поля равна: A₁₂ = q₀*∆φ, откуда dA = Udq = UIdt = I²Rdt = (U²/R)*dt;

Мощность тока: P = dA/dt = U*I = I²R = U²/R;

[A] = 1[Дж], [P] = 1[Вт]

Закон Ома для неоднородного участка цепи в интегральной форме, который является обобщенным законом Ома: I = (φ₁ – φ₂ + ε₁₂)/R.

Частные случаи:

1) Если на данном участке цепи источник тока отсутствует (нет сторонних сил), то получаем закон Ома для однородного участка цепи: I = U/R;

2) Если цепь замкнута (∆φ = 0), то получаем закон Ома для замкнутой цепи: I = ε/(R+r), ε – ЭДС, R и r – внешнее и внутреннее сопротивления;

3) Если цепь разомкнута, то I = 0 и ε₁₂ = φ₁ – φ₂, т.е. ЭДС в разомкнутой цепи равна разности потенциалов на ее концах.

4) В случае короткого замыкания сопротивление внешней цепи R = 0: I = ε/r.