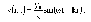7.3. Уравнение плоской бегущей волны

Прежде чем приступить к получению уравнения простейшего волнового движения необходимо сделать некоторые замечания о скоростях, фигурирующих в этом процессе, поскольку смысл и содержание этих величин отличаются от принятых в классической механике. При рассмотрении волнового движения различают три различных по смыслу и содержанию скорости.

1. Колебательная скорость частиц. Это скорость, которую приобретают частицы среды, будучи увлечёнными колебательным движением при прохождении волны. По сути это скорость колебаний частиц относительно положения равновесия.

2. Волновая или фазовая скорость. Это скорость, с которой перемещаются в пространстве поверхности одинаковой фазы, т.е. скорость с которой перемещаются горбы или впадины волн.

3. Групповая скорость. При сложении нескольких волн с разными длинами (частотами) и скоростями перемещения образуются группы волн (цуги, волновые пакеты). В реальности волны довольно редко наблюдаются в виде отдельных монохроматических компонент. В частности, вспышка белого света имеет сплошной спектр частот, поэтому характеризуется групповой скоростью распространения. Естественно со временем, вследствие разности фазовых скоростей для отдельных компонент в среде, пакет расплывается. Если среда отсутствует, такое имеет место быть для электромагнитных волн, то все частоты распространяются с одинаковыми скоростями. Для монохроматических волн значения фазовой групповой скорости совпадают.

Задача исследования волнового движения, как правило, сводится к определению амплитуды и фазы колебательного движения в различных точках среды, а так же изменение этих величин во времени. Задача решаема, если известен закон, по которому колеблется тело, являющееся источником волн и по каким законам происходит взаимодействие этого тела с окружающей средой. Правда, в ряде случаев информация об источнике волн является несущественной, потому что в место параметров колеблющегося тела задаётся расположение волнового фронта или волновой поверхности, а требуется определить состояние колебательного процесса в других точках среды.

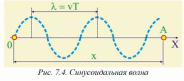
Рассмотрим простейший случай, когда волна распространяется в положительном направлении оси ОХ, при этом величину, характеризующую колебательные параметры частиц обозначим как у (рис. 7.4). Этой величиной может быть смещение относительно положения равновесия, отклонение давления или плотности среды. Пусть в начальный момент времени при t = 0, у = 0 и начальная фаза ф = 0

у = y₀ sin rat,

(7.2) ⁰

где ra = 2п/ T - циклическая частота, Т - период колебаний, у₀ - амплитуда колебаний, rat - аргумент синуса, определяющий значение колеблющейся величины в каждый момент времени, другими словами rat - фаза колебаний в точке О.

Точки А волновое движение достигнет га время

(7.3)

фаза колебаний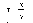 в этой точке определится как

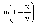(7.4)

Совмещая уравнения (7.4) и (7.2)

получим значение колеблющейся величины в точке А для момента времени t

(7.5)

где v - фазовая скорость волны. Если волна распространяется в обратном направлении, то уравнение (7.5) следует записать следующим образом

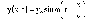
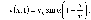
Для волны распространяющейся в обоих направлениях уравнение примет вид

(7.6)

(7.7)

Преобразуем последнее уравнение к виду

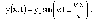
(7.8)

Циклическую частоту га можно выразить через частоту v, которая измеряется в герцах, или период Т, который измеряется в секундах, т.е.

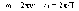
(7.9)

Поскольку изначально было введено предположение о постоянстве амплитуды и фазовой скорости, т.е. волна предполагалась плоской (поверхности равных фаз представляют собой плоскости). Расстояние, пройденное волной в течение периода, называется длиной волны

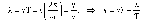
С учётом введённых обозначений уравнение (7.8) примет вид

(7.10)

(7.11)

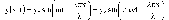
В последнем уравнении присутствует постоянная для данной волны величина 2п/Я, которая называется волновым числом, это векторная величина, модуль которой равен 2л/А, а направлен вектор волнового числа по направлению распространения волны

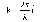
(7.12)

где i - единичный вектор, направленный по оси ОХ и измеряемый в единицах волнового числа, т.е. в м^- \

(7.13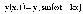

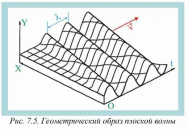
Уравнение плоской бегущей волны, распространяющейся в направлении оси ОХ, окончательно запишется в виде

На рис. 7.5 представлен

геометрический образ плоской бегущей волны, распространяющейся с фазовой скоростью v. Если поверхность равных фаз представляет сферу, то эту волну называют сферической, у которой амплитуда колебаний уменьшается обратно пропорционально расстоянию, уравнение (7.13) для сферической волны представится следующим

образом

(7.14)