Digital Fir Filters Without Tears
By Bill Windsor and Paul Toldalagi
Цифровые КИХ-фильтры без проблем
(В переводе Усенкова в.Н.)
Введение
Когда-то цифровые фильтры требовали особыx методов проектирования, дорогостоящую высокопроизводительную аппаратуру и сложное программное обеспечение для внедрения; по этой причине они использовались ограниченно. Сегодня, доступность недорогих высокоскоростных микросхем сигнальной обработки, таких как умножители и умножители-накопители в сочетании с простыми стандартизованными процедурами проектирования радикально упростило внедрение цифровых фильтров. Соответственно, если вам необходимы фильтры с крутизной выше 24 dB/oct, есть смысл применить цифровую фильтрацию.
Далее мы сравним цифровые и аналоговые фильтры, обсудим различные архитектуры цифровых фильтров и в качестве примера продемонстрируем пошаговый способ проектирования КИХ (нерекурсивных) фильтров. Будут даны ссылки для поиска информации по темам, которые затронуты неполно. (Терминология, сокращения и пояснения следуют далее по тексту).
Сравнение цифровых и аналоговых фильтров
Цифровая фильтрация интенсивно пробивается в модемы, радары, анализаторы спектра в оборудование обработки звука и изображений, и это имеет понятные причины: в сравнении с аналоговыми фильтрами цифровые обеспечивают большую крутизну, не требуют калибровки, более стабильны во времени, температуре и вариациях питания. Несложные программные коррективы позволяют изменять свойства цифровых фильтров «на лету»(так называемые адаптивные фильтры), в то время как аналоговые фильтры требуют аппаратных изменений.
Тем не менее, цифровые фильтры не удовлетворяют некоторым применениям. Аналоговая фильтрация обычно более выгодна в случаях крутизны до 24 dB/oct. Для диапазона выше 24…36 dB/oct выгоднее цифровые фильтры; для таких случаев многие разработчики считают разработку цифровых фильтров более простой. Шаблоны легко можно скорректировать программными изменениями. Кроме того, программная симуляция цифровых фильтров отражает реальные их возможности, в то время как при компьютерной симуляции аналоговых фильтров проявляется чувствительность к вариациям параметров компонентов, которые изначально не могут быть в нужной степени точными.
Базисные понятия цифровой фильтрации
Проектирование цифровых фильтров производится двумя основными способами: нерекурсивным (КИХ (FIR) конечный импульсный отклик) и рекурсивным (БИХ (IIR) бесконечный импульсный отклик). В рамках проектирования БИХ фильтров растет интерес к т.н. задержанной (lattice) топологии. Но прежде рассмотрим базисные понятия ЦФ.
ЦФ не столь сложны, как представляется. Предыдущие статьи от Analog Devices вводят читателей в курс дела (Vol.17,Number 1,1983, page 3 / Том 17, №1 1983, стр.3); ссылки в конце той и этой публикации позволят детализировать тему.
Хотя фильтрация обычно требуется для сглаживания сигналов во времени, многие разработчики лучше понимают принцип работы фильтров в частотной области. Спектр входного сигнала видоизменяется (перемножается с) передаточной характеристикой фильтра для изменения спектра выходного сигнала. Это видоизменение в частотной области эквивалентно свертке волновой формы и функции отклика во времени. Что такое свертка?
Чтобы понять процесс, сначала предположим идеальность передаточной функции H(f) в соответствии с рис. 1а. Функция H(f) имеет единичное усиление для сигналов, содержащих частотные составляющие в диапазоне от 0 до f1 Hz, где каждая частотная составляющая есть просто косинусоида соответствующей частоты. К примеру, сигнал cos(2*PI*3t) представляет компоненту единичной амплитуды при f=3Hz.
Рис. 1b иллюстрирует спектр сигнала X(f) со значением cos(2*PI*f2*t)+ cos(2*PI*f3*t). X(f) содержит две равные составляющие с частотами f2 и f3. Если нужно выделить составляющую f2, оставляя составляющие за f3, можно пропустить сигнал через ФНЧ. H(f) и есть такой фильтр, с частотой среза f1. Поскольку H(f) равен 1 на частоте f2 и 0 на частоте f3, умножение H(f) на X(f) дает 1*cos(2*PI*f2*t)+ 0*cos(2*PI*f3*t), или просто cos(2*PI*f2*t).
Таким образом, мы обсуждаем непрерывную временную функцию. Однако, в ЦФ имеют дело с выборками сигнала, где временная функция представлена конечным набором k дискретных значений, где k частота выборки. Поэтому косинусоида представляется в виде cos(2*PI*fn/k).
Прямое преобразование Фурье позволяет представить функции времени в виде функций частот, а обратное преобразование Фурье преобразует функцию частот в функцию времени. Аналогично, дискретное прямое преобразование Фурье переводит дискретную функцию времени в дискретную функцию частот, а обратное дискретное преобразование Фурье преобразует дискретную функцию частот в дискретную функцию ыремени.
Если функция частот образована двумя составляющими, например функцией сигнала и передаточной функцией , тогда соответствующая функция времени есть конволюция двух функций времени, т.е. форма сигнала во времени и передаточная функция определяют временной отклик.
Таким образом, теорема Фурье, приравнивая умножение в частотной области к конволюции во временной, позволяет непосредственно рассчитать временной отклик. Конволюция для дискретных функций времени
соответствует сумме откликов в частотной области для всех значений n.
Уравнение 2 содержит ряд умножений и сложений, которые, будучи выполнены соответствующим образом, представляют прохождение входного сигнала через фильтр нижних частот. Уравнение предполагает, что h(n) равно 0 для m<1 и m>N, что всегда справедливо для КИХ фильтров. Здесь N – это количество выборок h(n).
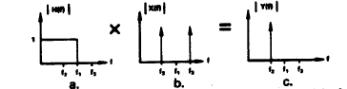
Рис.1. Только одна составляющая (с) остается после умножения функции фильтра (a) на сигнал (b).
Для вычисления уравнения 1, используя теорему Фурье, достаточно знания функций h(n) и x(n). Это обратное преобразование Фурье H(f) и X(f) на рис.1. Преобразование X(f) – простая косинусоида x(n)=cos(2PIf2n/k). Как будет показано, вычисления значений x(n) возможны при известных f2, f3 и частоты выборки k, определяемой скоростью работы АЦП при преобразовании входного сигнала x(t). Несколько сложнее вычислить значения h(n), которые называются коэффициентами фильтра. Но существуют специальные программы для их расчета, в том числе от Analog Devices.
Приведем практический пример уравнения 2, полагая фильтр 27 порядка с N=27. Тогда, выходное значение y(30), зависящее от 27 предыдущих значений x, будет таким:
y(30)=h(1)*x(29)+h(2)*x(28)+h(3)*x(27)+…+h(26)*x(4)+h(27)*x(3).
Физический смысл этого суммирования в том, что отклик фильтра на шаге составляется на основе суммирования 27 последовательно задержанных шагов, каждый из которых помножен на собственный коэффициент, чтобы построить результирующий отклик. Например, если каждый h(m) равен 1/27, отклик фильтра на шаге будет 27 ступенью …., для любой входной последовательности будет вычисляться скользящее среднее на интервале 27 шагов.
Далее обсудим вычисление коэффициентов.