Размышление о новой модели.

В ходе работы мы пришли к тому, что, фактически: действия гостя будут строго регламентированы относительно его изначальной стратегии и поведения официанта, он будет вести себя так, как велят ему отношение к социальной норме и его привычки, характер, в то же время на его поведение повлияет то, сколь предупредителен будет официант. Таким образом, он будет лишь реагировать на поведение официанта, ход же его будет совершён ещё до номинального начала игры, а точнее, мы можем говорить о том, что игра начинается ещё до того, как гость войдёт в ресторан. Ходом же его будет выбор той самой изначальной стратегии. Допущение это является достаточно серьёзным, так как фактически нивелирует возможность принятия решений на месте. С другой стороны, в нашей анкете около 50% респондентов упомянули, что высокие чаевые для них – попытка стимулировать официанта и в дальнейшем прилагать большие усилия при работе с ними. Фактически, это – предложение дальнейшей кооперации либо, в случае, если официант сработал, по мнению гостя, недостаточно хорошо, и чаевые не были даны или были уменьшены, демонстрация неудовольствия и урок на будущее. Нам это важно, потому что позволяет отнестись к позиции гостя как к всё же относительно нестабильной. Однако модель, построенная нами,

Построение новой модели.

Итак, в новой модели мы делаем допущения, изученные нами с помощью опроса. Существуют люди, изначально готовые платить чаевые в любом случае, те, кто платят по ситуации и те, кто не платят их никогда, причём соотношение их количеств примерно постоянно. Склонность к чаевым в данном случае является основополагающим фактором, от которого зависит, получит ли официант дополнительное вознаграждение. Качество обслуживания, несмотря ни на что, важный (хоть, быть может, и не ключевой) фактор, влияющий если уж не напрямую на выплату/невыплату чаевых, то как минимум – на их размер. Наконец, сделаем ещё одно запасное допущение: официант в этой игре, скорее всего, будет рискофилом, т.е. его полезность от чаевых будет всегда выше, чем потери полезности от приложенных усилий. Допущение это основывается на том факте, что люди, идущие на профессию официанта, знают о том, что их общая заработная плата будет в высокой степени зависеть от чаевых и принимают это, поступая на работу.

В то же время нельзя забывать и о последовательности действий. Она продемонстрирована на дереве игры, расположенном ниже. Изначально ситуация зависит от того, какой склонностью к чаевым характеризуется гость, который зашёл в ресторан. Как мы говорили выше, в нашей игре это можно считать изначальной стратегией этого игрока. Не обладая информацией об этой склонности, официант, тем не менее, должен разработать оптимальную для себя стратегию. Он решает, какие усилия будет прилагать, и лишь только после этого гость решает, какие чаевые ему, в конечном счёте, дать. При этом мы сначала хотели ввести в игру показатель t0, обозначающий минимальные чаевые, возможно равные нулю, но потом сделали очередное предположение, что гость не станет снижать чаевые ниже некоего среднего уровня (судя по нашей анкете, уровень этот находится где-то в районе 4,5%), а в случае неудовлетворённости вообще откажется давать чаевые, вместо того, чтобы ещё больше снизить их. Это – ещё одна социальная норма общества, кроме того, согласовывающаяся с результатами анкеты, поэтому мы приняли её в задачу как условие. Наша модель будет основываться на типе гостя в отношении склонности к уплате чаевых и, конечно, на усилиях официанта. Для удобства примем, что официант предпринимает либо максимум усилий, либо половину усилий, либо вообще их не предпринимает, а полезность гостя от обслуживания пропорционально зависима от них (пропорциональную корреляцию наш допрос не слишком строго, но демонстрирует). И, что наиболее важно, варианты распределения склонности гостя будут иметь веса соответственно проведённому нами опросу. Для удобства округлим количество людей, не склонных давать на чай, до 10% (от изначальных 8%).

Ещё раз опишем модель игры. Как и в первой, представленной нами, официант (О) обслуживает гостя ресторана (Г). Официант может обслужить гостя хорошо или плохо (приложив или, соответственно, не приложив усилий), гость может дать или не дать официанту чаевые. Мы обозначили буквами: U – полезность гостя от заказа, K (дабы отличить показатель от Q в первом варианте модели) – полезность гостя от высокого уровня обслуживания, T – высокие чаевые, t – чаевые среднего размера, e – усилия, затрачиваемые официантом ради достижения высокого уровня обслуживания. Кроме того, мы вставили в таблицу пропорциональное уменьшение e и K, подразумевая приложение средних усилий (для наглядности принятых за половину полных) официантом и соответствующее снижение полезности, полученной от обслуживания гостем. Напомним, выигрыш гостя включает в себя U и K (либо K/2), а также затраченную сумму чаевых (Т или t) с отрицательным знаком. Официант же получает полезность от чаевых (T либо t) и несёт потери полезности из-за затраченных на обслуживание усилий (e или e/2).

Кроме всего прочего, нужно учесть, что, в соответствии с нашими предпосылками: t > e >> e/2, T > t (откуда T >> e),

T > 2t, что чрезвычайно важно и следует из таблицы в приложении №7,

K/2 – t < K – T, т.е. как минимум K > 2T – 2t, а в общем – показатель K сильно выше, чем все остальные, кроме, скорее всего, U. Мы будем считать, что K > 1,5 T, что, в общем и целом, сообразуется с результатами опроса.

Модель будет выглядеть следующим образом:

		Официант
	Варианты	e = 1	e = 1/2	e = 0
Гость	Всегда даёт на чай (α = 0,1)	U + K – T; T - e	U + K/2 – t; t – e/2	U – t; t
	Действует по ситуации (α = 0,8)	U + K – T; T - e	U + К/2 – t; t – e/2	U; 0
	Никогда не даёт на чай (α = 0,1)	U + K; - e	U + K/2; -e/2	U; 0

Найдём равновесие модели.

Начнём с гостя. Его поведение в данном случае, как уже было упомянуто, в по условию модели полностью регламентируется поведением официанта и его изначальной стратегии. Однако обратим внимание: если бы игра была одновременной и исключала все социальные феномены, доминирующей стратегией для гостя было бы не платить чаевые вовсе, т.к. это было бы максимально выгодно при любом поведении официанта.

Обратимся к поведению официанта. Он ходит вторым, однако фактически не знает ничего о ходе гостя. Нам здесь важно, что с учётом упомянутых предпосылок доминирующей стратегией для официанта в случае если гость всегда даёт на чай либо действует по ситуации будет - прилагать максимум усилий. Если же гость никогда не даёт на чай, то и официанту не имеет смысла прилагать усилия. Однако такое случается лишь в 1 шансе из 10. Мы предполагаем, что официанты хорошо представляют себе примерное соотношение таких типов гостей на основе собственного опыта, а значит, они знают, что в 9 из 10 случаев им следует рискнуть ради большей полезности в итоге. Т.к. наш агент – рискофил, итогом этого будет положение, при котором усилия он будет прикладывать всегда. Если следовать по этой системе дальше, то мы получаем 3 равновесия для гостя, т.к. он, фактически, не участвует в выборе, стратегии у него нет, есть лишь тип. Итак, в зависимости от своего типа гость либо будет платить большие чаевые, либо не будет платить вовсе. Итого общая полезность гостя, не платящего чаевые, составит U + K, а общая полезность гостя, платящего чаевые – U + K – T. Общая полезность официанта будет равна Uо = 0,9 * (T-e) + 0,1 * (-e) = 0,9 T – e.

Ещё раз отметим, что равновесие Нэша без учёта социальных норм и наших предпосылок было бы на уровне U + K; - e, потому что доминирующей стратегией для официанта будет прилагать усилия, ожидая чаевые, а для гостя – их не платить. Возможно, для приведения ситуации к реальной нам необходимо будет внести ещё один фактор, выражающий полезность чисто моральную от факта уплаты чаевых (что, судя по нашей анкете, людям очень даже свойственно). Однако, этот фактор требует дальнейшего и очень глубокого изучения, невозможного на уровне студенческой работы.

Рассмотрим дерево игры в таком распределении. В него нам необходимо ввести, кроме всего прочего, эффект ситуационный, отметим его как N. Это могут быть настроение гостя, антураж ресторана или наличие мелочи в кошельке. Такой эффект может как увеличить желание дать чаевые, так и уменьшить его, если эффект отсутствует. Согласно нашей анкете, ситуационный эффект может иметь очень большое значение.

Для упрощения поставим действие N перед действием официанта. Впрочем, хронологически это будет верным. Пунктир обозначает, что официант не знает, удачно ли расположение ситуационных факторов.

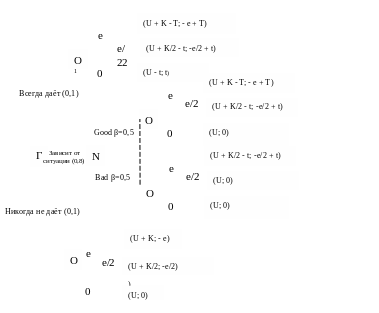
Отметим, что официант попадает в первую точку О с вероятностью 0,1, во вторую и третью с вероятностью 0,4 и 0,4 соответственно, в четвёртую – также с вероятностью 0,1. Красным выделены доминирующие стратегии в каждом случае. В итоге официант и гость придут к тому же, к чему пришли в матрице игр.

Однако отметим, что данная схема не слишком точна, она лишь чрезвычайно примерно указывает, как будут действовать индивиды. В завершении нашего анализа мы хотели бы продемонстрировать кульминацию нашей работы, наиболее точную и полную на данный момент модель, позволяющую с высокой точностью высчитать вероятность, с которой гость даст официанту на чай.

Мы же выяснили, что детерминанты чаевых – это изначальная склонность к ним, общие причины, ситуационные причины и обслуживание. При изначальной склонности к выплате чаевых вероятность получить на чай для официанта будет равна 1, при склонности к отказу в чаевых – она будет равна 0. Дальше рассматривать эти ситуации нецелесообразно, тем более, что мы уже дважды это сделали, поэтому имеет смысл рассмотреть ситуационную стратегию и, соответственно, влияние общих причин (с которыми индивид заходит в ресторан), ситуационных причин (которые индивид оценивает, уже находясь в ресторане) и сервиса. Дадим этим факторам веса α, β и γ соответственно и учтём, что α + β + γ = 1, фактор общих причин обозначим как А, ситуационные причины мы уже обозначили как N, а обслуживание – как e. Зададим границы измерения. Общие причины могут влиять на изначальную склонность к выплате чаевых и либо создавать её, либо, напротив, уменьшать. Пользуясь этой предпосылкой, возьмём A{0; 1} (склонность отсутствует или всё же есть), N{0; 1} (обстоятельства сложились для официанта удачно или неудачно), e{0; 0,5; 1} (сколько усилий приложил официант). При этом 0 < A* α + N * β + e * γ < 1 (граничные значения входят в отрезок, являясь его вершинами. Для каждой конкретной ветви мы легко можем посчитать значения коэффициентов, показывающих разброс значений, но вот коэффициента вероятности нет. Мы предполагаем, что склонность к чаевым важнее обслуживания, а обслуживание важнее внутренних причин, но выразить их в числом эквиваленте пытаться пока не будем. Один из авторов данной работы предложил веса α = 0,5; β = 0,2 и γ = 0,3. Такое распределение достаточно репрезентативно, что было проверено на примере. Однако, сама по себе идея подбора в высшей степени ненаучна. Поиск коэффициентов α, β и γ мы планируем продолжить в следующих работах. А пока мы продемонстрируем работу модели в общем виде и найдём вероятность, с которой индивид получит чаевые. Можно сделать гипотетическое предположение, что при значении t* > x, где x – некая близкая к 1 доля (предположим, 0,75 или 0,7, а может даже 0,6), чаевые, получаемые официантом, будут увеличенными. С другой стороны, тогда при t* < y, где y – некая близкая к 0 доля (скажем, 0,15), гость чаевых может не дать вообще. Доли, хоть и примерные, взяты не из головы, но основаны на опросе. Данные, использованные для таблицы со средними чаевыми при меняющихся условиях и качестве обслуживания подтвердили, что подавляющее большинство респондентов откажется от чаевых при минимальном коэффициенте качества обслуживания. Сама таблица также демонстрирует, насколько низки даже средние чаевые при плохом сервисе, и как быстро они растут, начиная от средних.

А = 1

e = 0

Г

(7)

Г

1

Г

(8)

0

N

А = 0

e = 1

Г

(9)

1

N

e = 0,5

О

Г

(10)

0

1

e = 0

N

Г

(11)

0

Г

(12)

Для каждого случая найдём t*, вероятность того, что официант получит чаевые.

1. t* = 1 * α + 1 * β + 1 * γ = 1

2. t* = 1 * α + 0 * β + 1 * γ = 0,8

3. t* = 1 * α + 1 * β + 0,5 * γ = 0,85

4. t* = 1 * α + 0 * β + 0,5 * γ = 0,65

5. t* = 1 * α + 1 * β + 0 * γ = 0,7

6. t* = 1 * α + 0 * β + 0 * γ = 0,5

7. t* = 0 * α + 1 * β + 1 * γ = 0,5

8. t* = 0 * α + 0 * β + 1 * γ = 0,3

9. t* = 0 * α + 1 * β + 0,5 * γ = 0,35

10. t* = 0 * α + 0 * β + 0,5 * γ = 0,15

11. t* = 0 * α + 1 * β + 0 * γ = 0,2

12. t* = 0 * α + 0 * β + 0 * γ = 0

Не зная, с каким гостем он имеет дело и как гость относится к ситуации, агент всё равно рискнёт и будет обслуживать его по высшему классу, надеясь на максимальные чаевые. В случае, когда гость склонен к чаевым, официант получит их, скорее всего, увеличенные, с вероятностью 0,9. В случае, когда гость не склонен к чаевым, официант получит чаевые с вероятностью 0,4. Итого, доминирующая стратегия – вновь в сочетании максимальных усилий и максимальных чаевых.