Практическое занятие №2. Геометрическая вероятность.

1. После прошедшего урагана на участке между 40-м и 70-м километрами телефонной линии произошел обрыв провода. Какова вероятность того, что разрыв произошел между 45-м и 50-м километрами линии?

2. Найти вероятность того, что точка, наудачу поставленная в треугольник. Попадет в меньший треугольник, полученный после проведения одной из средних линий большего треугольника.

3. На плоскости проведены две концентрические окружности, радиусы которых равны 3см и 5см соответственно. Какова вероятность того, что точка, наудачу брошенная в большой круг, попадет в кольцо, образованное этими окружностями?

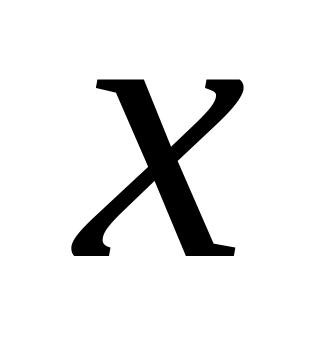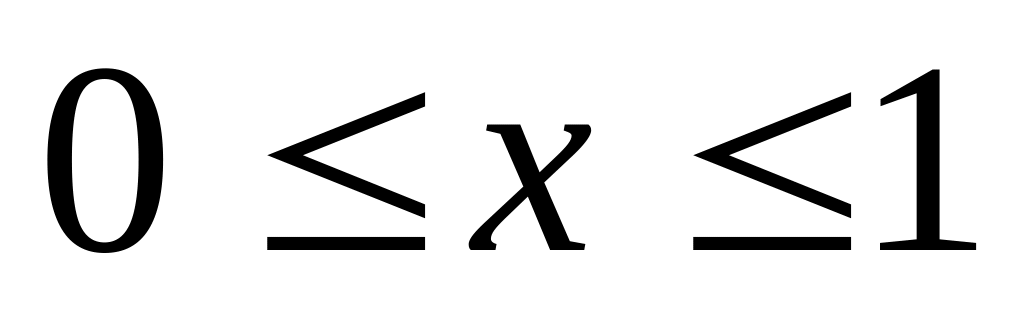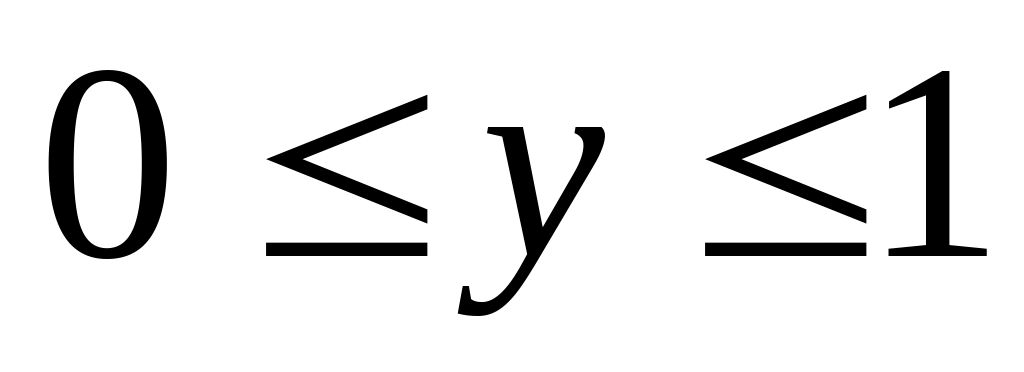4. Задуманы два числа и , такие, что , . Какова вероятность того, что 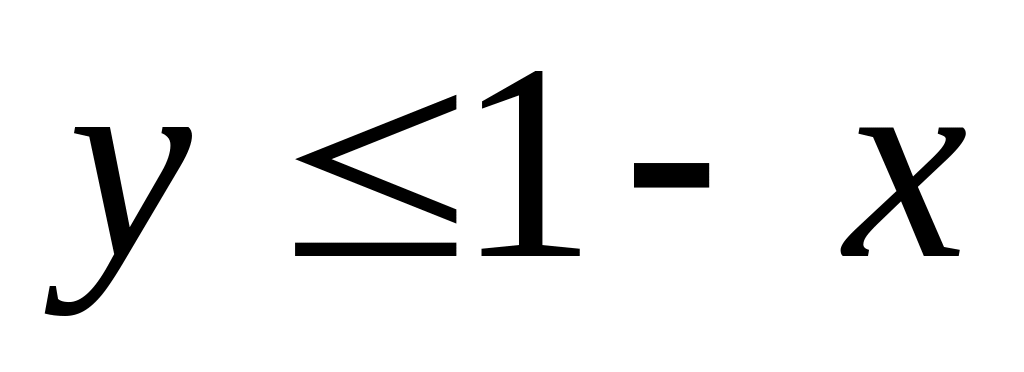и ?

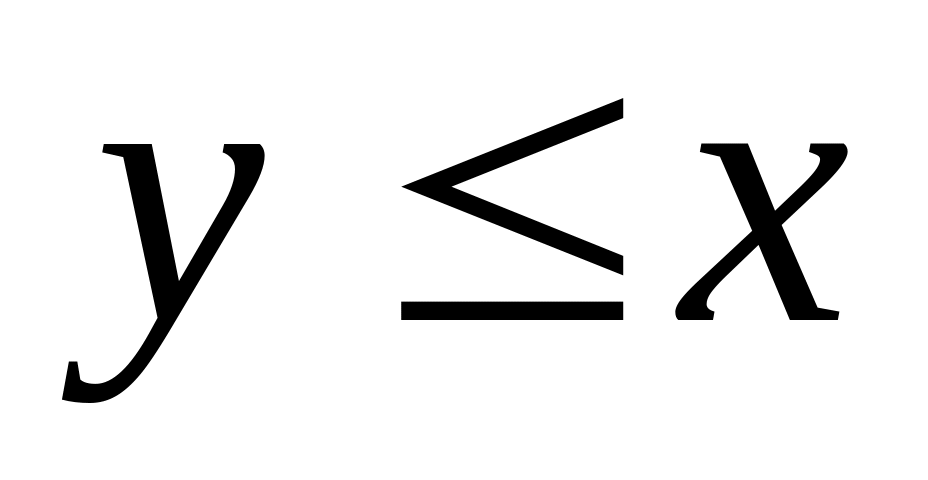5. Наудачу взяты два неотрицательных числа и , каждое из которых не больше единицы. Найти вероятность того, что сумма этих чисел не превышает единицы, произведение не больше .

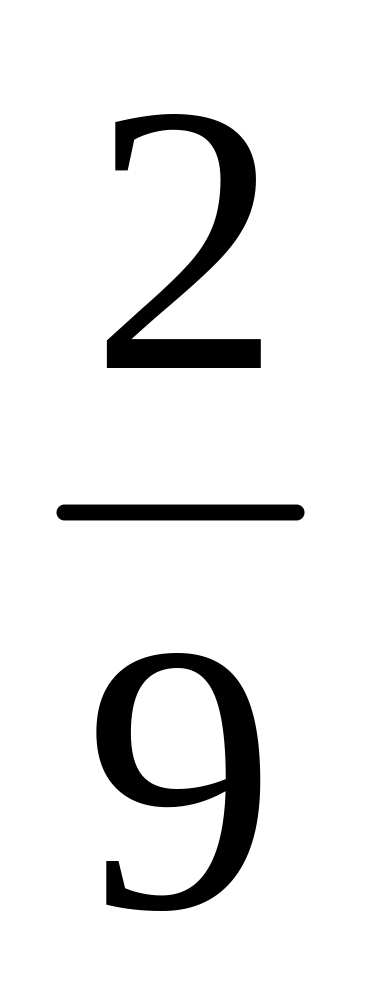6. На перекрестке установлен автоматический светофор, в котором одну минуту горит зеленый свет и полминуты красный, а затем снова одну минуту зеленый и полминуты красный и т.д. в случайный момент времени к перекрестку подъезжает автомобиль. Какова вероятность того, что он проедет перекресток без остановки?

7. К причалу для высадки пассажиров в течение ближайшего часа в случайные моменты времени должны подойти два катера. Одновременное причаливание двух катеров невозможно. Время высадки пассажиров с первого катера составляет 10 минут, а со второго катера – 20 минут. Найти вероятность того, что одному из катеров придется ожидать освобождения причала.

Ответы.

1. .2. 0,25. 3. 0,64. 4. 0,25. 5. 0,4873. 6. . 7. 0,43.

Задачи для домашнего задания№2.

1. На отрезок, имеющий длину 40 см, помещен меньший отрезок длиной 15 см. найти вероятность того, что точка, наудачу поставленная на больший отрезок, попадет также и на меньший отрезок.

2. Найти вероятность того, что точка, наудачу поставленная в равнобедренную трапецию с основаниями , 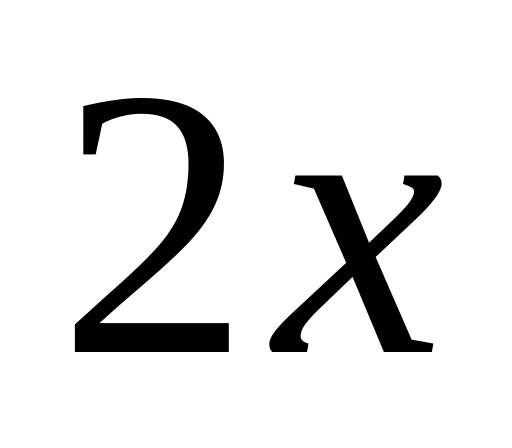и высотой , попадет в квадрат, образованный при приведении двух высот.

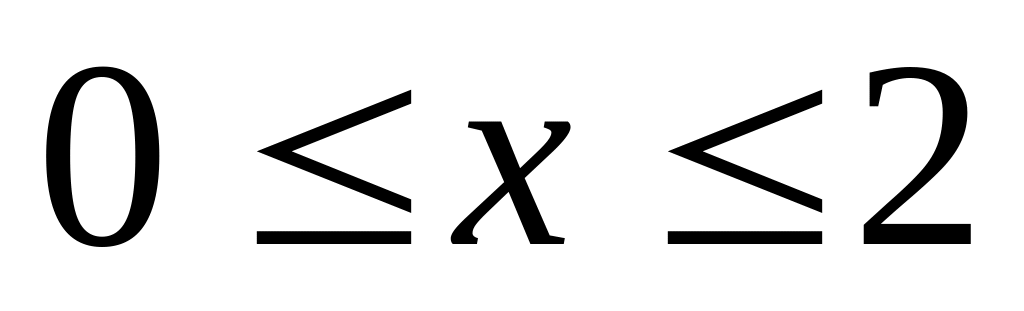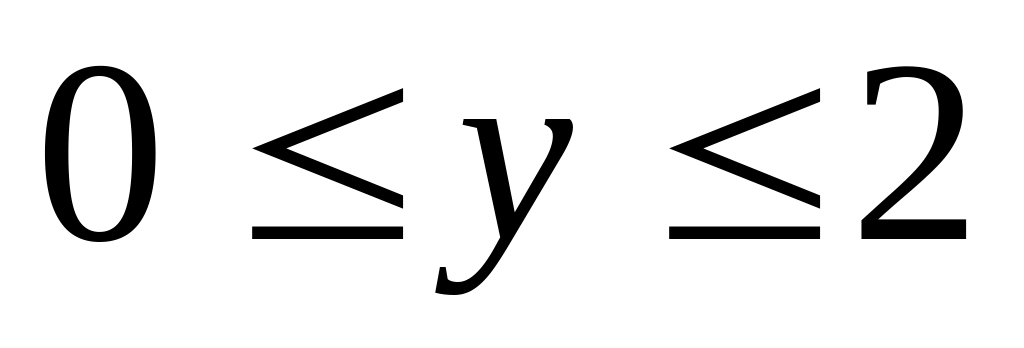3. Задуманы два числа и , такие, что , . Какова вероятность того, что ?

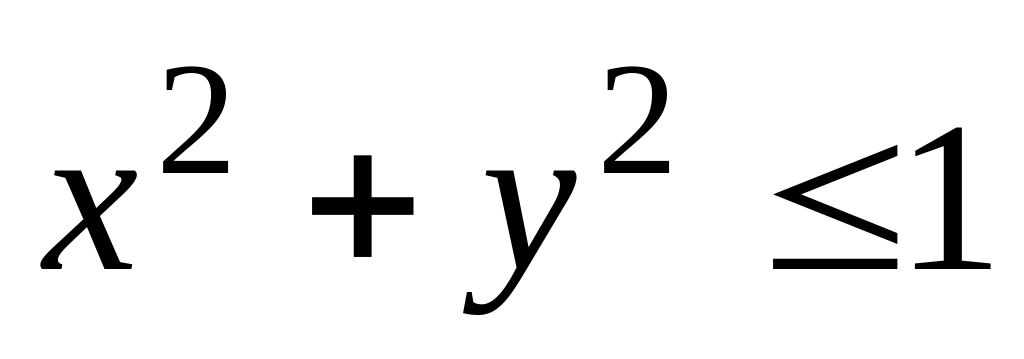4. Внутрь круга радиуса R наудачу брошена точка. Найти вероятность того, что точка окажется внутри вписанного в этот круг правильного треугольника.

5. Сергей и Дмитрий договорились о встрече между 11.00 и 12.00. каждый приходит в случайный момент указанного промежутка и ждет появления другого до истечения часа, но не более 15 минут, после чего уходит. Найти вероятность того, что встреча состоялась.

6. Коэффициенты p и q квадратного уравнения 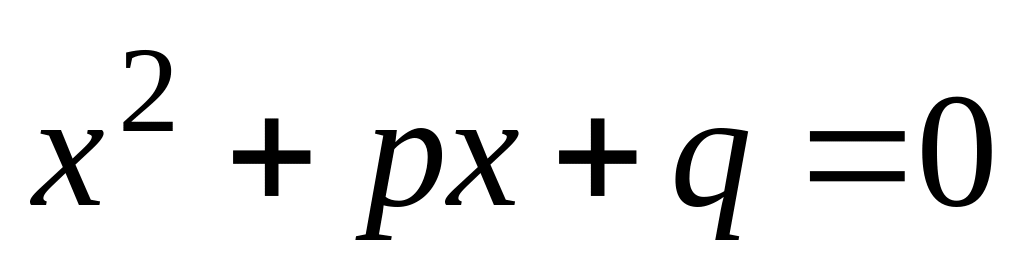выбирают наудачу в промежутке . Какова вероятность того, что корни этого уравнения будут действительными числами?

ОТВЕТЫ

1. . 2. . 3. . 4. . 5. . 6. .

Лекция №2

§6. Основные теоремы теории вероятности.

6.1. Теоремы сложения и умножения вероятностей событий.

Определение 10. Суммой или объединением двух событий А и В называется событие, состоящее в наступлении хотя бы одного из событий А, В и обозначаемое как А+В или А В.

Определение 11. Пересечением или произведением событий А и В называется событие, состоящее в совместном наступлении событий А, В и обозначаемое как АВ или А В.

Замечание 1. Для того чтобы не ошибиться, с чем имеем дело, произведением или суммой, можно использовать простое правило: если при описании события используем союз «и», то это произведение, если союз «или», то это сумма.

Теорема 1.(Теорема сложения вероятностей для несовместных событий). Пусть события и несовместны, тогда

.

Следствие 1. Если события попарно несовместны, то

.

Следствие 2. Если события образуют полную группу, то вероятность их суммы равна 1, т.е.,

=1.

Следствие3. Сумма противоположных событий равна 1, т.е.,

.

Замечание 2. Следствие 3 удобно использовать при вычислении вероятности появления хотя бы одного события.

Теорема 2. (Теорема сложения вероятностей для совместных событий). Если события и совместны, то

.

Определение 12. Зависимыми и независимыми называют два события, если вероятность одного из них меняется или не меняется, в зависимости от того произошло уже другое событие или не произошло.

Теорема 3. (Теорема умножения вероятностей для независимых событий). Если события и независимы, то

.

Определение 13. События называются независимыми в совокупности, если каждое из них независимо по отношению к любому из остальных и по отношению к любому произведению остальных.

Следствие 1. Если события независимы в совокупности, то

.

Следствие 2. Если события независимы в совокупности, то вероятность того, что наступит хотя бы одно из них, равна

, где .

Определение 14. Вероятность Р(В/А) наступления события В при условии наступления в то же время события А называют условной.

Теорема 4. (Теорема умножения вероятностей для зависимых событий). Если события и зависимы, то

.

Следствие 1. Если события зависимые, то

.

Следствие 2. .

Рассмотрим несколько примеров на применение этих теорем.

Пример 6.1. Три стрелка делают по одному выстрелу по мишени. Известны вероятности попаданий: , , . Найти вероятности следующих событий:

1) – мишень поражена одним выстрелом;

2) – мишень поражена двумя выстрелами;

3) – мишень поражена тремя выстрелами;

4) – мишень не поражена;

5) – мишень поражена хотя бы одним выстрелом.

Решение. Введем следующие события: – попал первый стрелок, – попал второй стрелок, – попал третий стрелок.

1) Событие – мишень поражена одним выстрелом означает, что в мишень попал только один из стрелявших, т.е., первый стрелок попал, второй и третий не попали или второй попал, первый и третий промахнулись, или первый и второй стрелки не попали, а третий был точен. Составим событие из событий , , и им противоположных, используя понятие суммы и произведения событий и замечание 1.

_.

События , , несовместны и независимы, поэтому воспользуемся теоремами 1 и 3.

2) Рассуждая аналогично п. 1), составим событие А₂:

.

0,8·0,6·(1-0,9)+0,8·(1-0,6)·0,9+(1-0,8)·0,6·0,9=0,444.

3) Событие означает, что попали все стрелки: и первый и второй и третий, значит

Тогда по теореме 3: 0,8·0,6·0,9=0,432.

4) Событие – мишень не поражена, означает, что все стрелки промахнулись, т.е.

.

Тогда по теореме 3: (1-0,8)(1-0,6)(1-0,9)=0,008.

5) Для вычисления вероятности события воспользуемся замечанием 2. Введем противоположное событие - все промахнулись (заметим, что событие совпадает с событием ). Тогда =1-0,008=0,992.

Пример 6.2. Из 50 вопросов к экзамену два студента выучили 40. Найти вероятность того, что оба студента получат по вопросу, который они выучили.

Решение. Событие – первый студент получил вопрос, который выучил, событие – второй студент получил вопрос, который выучил. События и – зависимые, поэтому воспользуемся теоремой 4:

.

6.2. Формулы полной вероятности и Байеса.

Теорема 5. (Формула полной вероятности). Пусть некоторое событие А может произойти лишь вместе с одним из n несовместных событий H₁, H₂, …, H_{n ,} составляющих полную группу (назовем их гипотезы). Тогда вероятность появления события А в этом испытании вычисляется по формуле

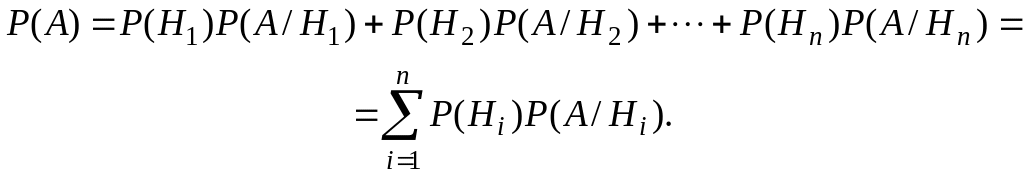
Разберем пример на применение этой теоремы.

Пример 6.3. Задача о переливании крови. При переливании крови надо учитывать группы крови донора и больного. Человеку, имеющему четвертую группу крови, можно перелить кровь любой группы; человеку со второй или третьей группой можно перелить кровь либо той же группы, либо первой; человеку с первой группой крови можно перелить кровь только первой группы. Среди населения 33,7% имеют первую группу, 37,5% - вторую, 20,9% - третью, 7,9 % - четвертую группы крови. Найти вероятность того, что случайно взятому пациенту можно перелить кровь случайного донора.

Решение. Воспользуемся теоремой 5. Пусть событие – пациент выжил, т.е. группа крови ему подошла. Возможны следующие гипотезы:

H₁ – у пациента первая группа крови;

H₂ – у пациента вторая группа крови;

H₃ – у пациента третья группа крови;

H₄ – у пациента четвертая группа крови.

Найдем вероятности гипотез: исходя из условий задачи =0,337, =0,375, =0,209, =0,079.

Следует обязательно проверять, чтобы сумма вероятностей гипотез равнялась единице.

Контроль:

+ + + =0,337+0,375+0,209+0,079=1.

Найдем условные вероятности события .

Если имеет место гипотеза , т.е. у пациента первая группа, значит, ему подходит только донор с первой группой, тогда , т.к. 33,7% населения имеют первую группу.

Если имеет место гипотеза , то пациенту подходи донор с первой или второй группой крови, следовательно, .

Если имеет место гипотеза , то пациенту подходи донор с первой или третьей группой крови, следовательно, .

Если имеет место гипотеза , то пациенту подходи донор с любой группой крови, следовательно, .

Найдем полную вероятность события А.

Заметим, что при решении задачи мы не учитывали такой важный аспект при переливании крови, как резус-фактор.

Пример 6.4. В двух урнах находится по 3 белых и 7 красных шаров. Из первой урны наудачу извлекают один шар и кладут его во вторую урну. После этого из второй урны извлекают наудачу два шара. Найти вероятность того, что оба они окажутся красными.

Решение. В данном случае гипотезами являются два альтернативных события: H₁ – из первой урны во вторую переложен белый шар; H₂ – переложен красный шар. По условию =0,3; =0,7.

От того, какое из этих событий произошло, зависит соотношение белых и красных шаров во второй урне, а следовательно, и вероятность события А, состоящего в извлечении из второй урны двух красных шаров.

Найдем условные вероятности события А.

Если имела место гипотеза H₁, то во второй урне окажется 4 белых и 7 красных шаров, следовательно,

.

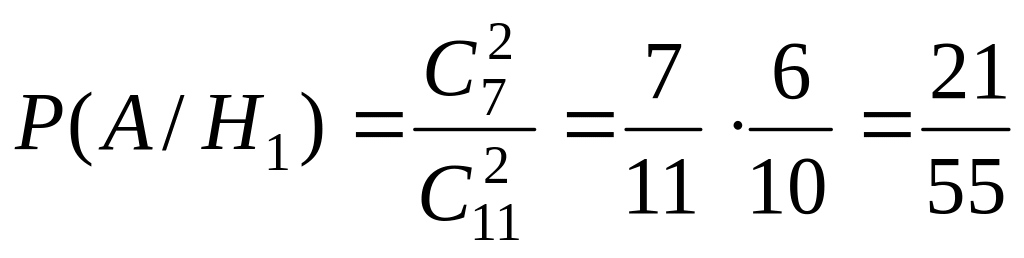Если же произошло событие H₂, то изменится количество красных шаров во второй урне – их станет 8, следовательно,

Теперь по формуле полной вероятности находим вероятность события А:

Пусть по прежнему производится испытание, в результате которого событие А может произойти лишь вместе с одним из n несовместных событий H₁, H₂, …, H_n с вероятностями , . Допустим, что событие А произошло, но с какой из гипотез – неизвестно. Возникает вопрос: каковы теперь вероятности гипотез после того, как стал известен результат испытания?

Ответ на поставленную задачу дает следующая теорема.

Теорема 6. (Формула Байеса). Пусть случайное событие А может произойти лишь вместе с одним из n несовместных событий H₁, H₂, …, H_{n ,} составляющих полную группу, и в результате испытания событие А произошло. Тогда вероятность того, что оно произошло вместе с гипотезой H_i, вычисляется по формуле

где - полная вероятность события А.

Рассмотрим задачу на применение этой формулы. Вернемся к задаче о переливании крови (пример 2.3).

Пример 6.5. Пусть в условиях примера 2.3 событие А произошло – переливание крови прошло успешно. Какова вероятность того, что у пациента была третья группа крови?

Решение. По формуле Байеса получим условную вероятность гипотезы H₃:

.

Формула Байеса играет значительную роль в практических приложениях: она используется в теории стрельбы, в теории распознавания образов, технической диагностике и т.д.