§2. События, их классификация.

Теория вероятностей занимается изучением не любых событий, которые в житейской практике называются случайными, а только тех из них, которые обладают определенными свойствами:

1) события могут быть осуществлены, в принципе, неограниченное число раз, причем, в неизменных условиях;

2) события должны обладать статистической устойчивостью.

Подчеркнем, что теория вероятностей не занимается изучением уникальных явлений, которые не допускают повторений.

Дадим основные определения:

Определение 1. Испытанием называется комплекс некоторых условий, которые можно осуществлять неограниченное число раз.

Определение 2. Событием называется некоторый исход испытания.

Определение 3. Событие называется достоверным, если в результате испытания оно обязательно произойдет.

Например, при подбрасывании игральной кости выпадет число не более шести.

Определение 4. Событие называется невозможным, если в результате испытания оно не может произойти.

Например, при подбрасывании игральной кости выпадет число 8.

Определение 5. Событие, которое в результате данного испытания может произойти, а может и не произойти, называется случайным.

Например, при подбрасывании игральной кости выпадет число 3.

Определение 6. Совместными называются два события, из которых одно не исключает другого, т.е. они могут произойти оба в одном испытании.

Например, события: А - занять первое место в соревновании по бегу, В – побить мировой рекорд в соревновании по бегу являются совместными.

Определение 7. Несовместными называются два события, которые не могут произойти оба в одном испытании.

Например, события: - получить «5» на экзамене по теории вероятностей в ближайшую сессию, – получить «3» на экзамене по теории вероятностей в ближайшую сессию, являются несовместными.

Определение 8. Полной группой событий называется множество событий несовместных между собой, и таких, что одно из них обязательно произойдет.

Полная группа событий обозначается так: {А, В, С} – события А, В, С образуют полную группу.

Определение 9. Противоположными называются два события, одно из которых приходит тогда и только тогда, когда не происходит другого.

Событие, противоположное событию , обозначается так: . Противоположные события образуют полную группу, т.е.

Например, события: А – попасть в мишень и – промахнуться, являются противоположными, т.е. В= .

§3. Вероятность случайного события.

3.1. Классическое определение вероятности события.

Вероятностью события называется числовая характеристика степени возможности появления события в испытании, которое можно повторять неограниченное число раз.

Если количество всех исходов испытания конечно и все исходы между собой равновозможны, то вероятность события А в этом испытании вычисляется по формуле

, (3.1)

где - число всех исходов испытания, - число благоприятных исходов, т.е. тех исходов, в которых появляется событие А.

Запишем эту формулу по-другому

(3.2)

Пример 3.1. Колода 36 карт. А - событие, состоящее в том, что наудачу вытащенная карта окажется бубновой мастью.

По условию, , , тогда

.

Основные свойства вероятности события:

1º. Пусть B - достоверное событие, т.е. , значит

.

2º. Пусть С - невозможное событие, т.е. значит

.

3º. Пусть А - случайное событие, т.е. , значит

.

4º. .

Вывод:

3.2. Геометрическое определение вероятности события.

Пусть область часть области , т.е. . Событие А - точка, наудачу брошенная в D, попадает и в d. Если вероятность попадания точки в d не зависит от ее места положения в D, то

.

Частные случаи:

1. Одномерный случай .

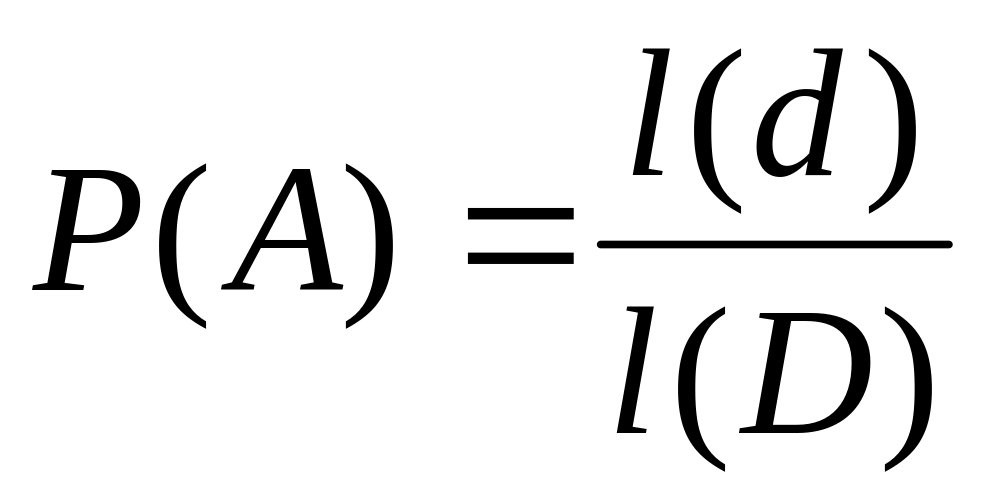2. Двухмерный или плоский случай .

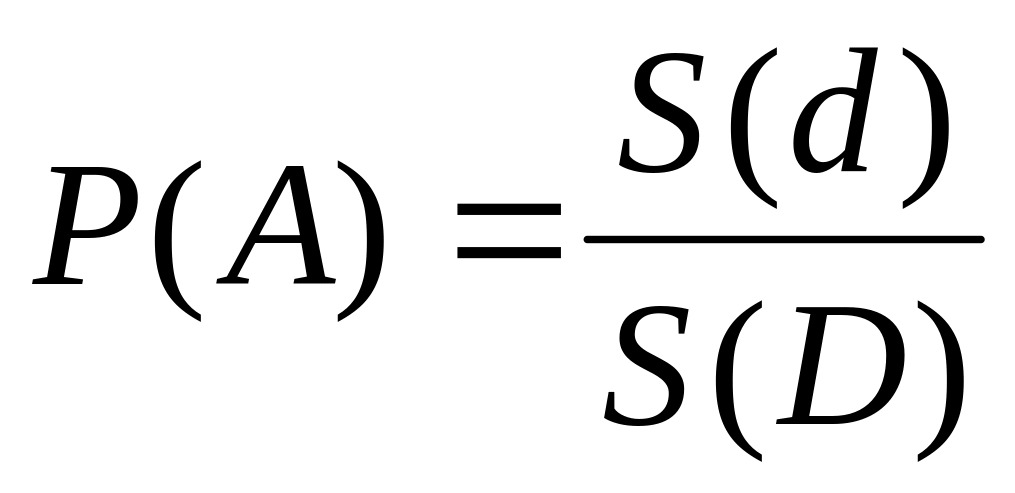3. Трехмерный случай .
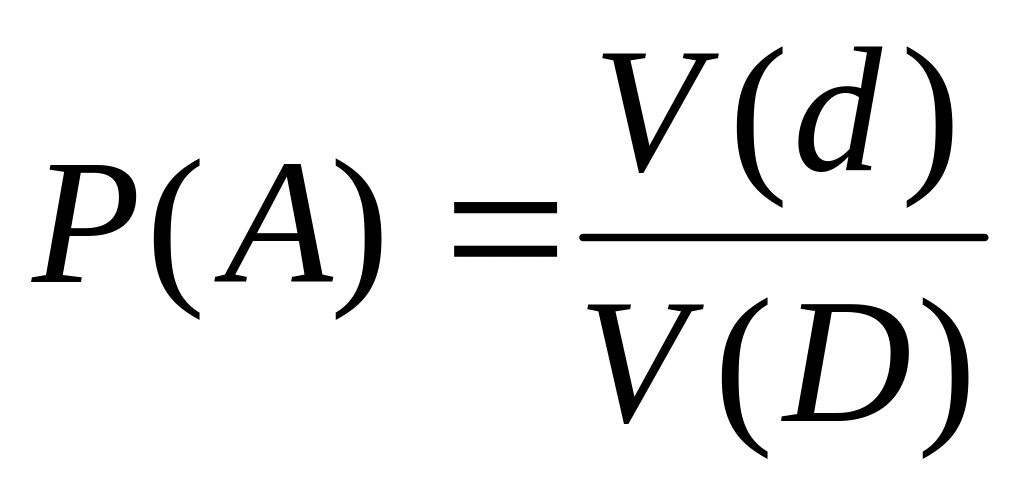