Закономірності руху тіл у середовищах
Основним критерієм оцінки параметрів руху частинки при гравітаційних процесах (гідравлічна класифікація, відсадка, важкосередовищна і ґвинтова сепарація, згущення та ін.) служить швидкість її переміщення в середовищі. Якщо швидкість руху тіла щодо середовища невелика, відбувається безвідривне обтікання частинки потоком рідини, опір руху тіла обумовлено в основному силами тертя. Зі збільшенням швидкості руху обтікання тіла відбувається з вихроутворенням, що стає тим інтенсивніше, чим більша швидкість обтікання і шорсткість тіла. У цьому випадку переважає інерційний опір. Опір тертя переважає при ламінарних режимах руху, інерційний – при турбулентних.
Вивчення закономірностей руху тіл у середовищах здійснюється з урахуванням вільних і стислих умов. Результати вивчення закономірностей руху частинок у рідинах, суспензіях і газах використовуються при розробці теорії гравітаційних процесів, розрахунку апаратів гравітаційного розділення.
Закономірності вільного руху тіл у середовищах
Вільним називається падіння одиничних ізольованих одна від одної частинок у необмеженому об'ємі середовища.
Швидкість вільного падіння тіл у середовищах визначається взаємодією сил:
- гравітаційної
F1 = πd3 (δ – Δ) g / 6, Н, (2.29)
де d – еквівалентний діаметр кулі рівновеликої за об’ємом реальному тілу, м; δ – густина тіла, кг/м3; Δ – густина середовища, кг/м3; g – прискорення вільного падіння, м/с2;
- гідродинамічного опору
F2 = ψV2d2Δ, (2.30)
де ψ – коефіцієнт гідродинамічного опору середовища тілу, що рухається; V - швидкість тіла в середовищі, м/с.
Сила опору середовища тілу, що рухається в ній, залежить від режиму руху – ламінарного або турбулентного. Режим руху характеризується безрозмірним параметром – числом Рейнольдса:
Re = VdΔ /μ, (2.31)
Ламінарний режим обтікання відбувається при невеликих швидкостях руху (Re <1) частинок малої крупності (d < 0,1 мм). При ламінарному обтіканні елементарні шари середовища плавно сходять за тіло і не утворюють вихрів. У цьому випадку сила в’язкісного опору середовища обумовлюється силами тертя, що виникають у ній унаслідок різниці швидкостей руху окремих елементарних шарів, і описується законом Стокса:
F2 = 3πμVd. (2.32)
Якщо динамічний коефіцієнт в'язкості μ представити з використанням формули (2.31) як:
μ = VdΔ / Re,
то вираз (2.32) можна перетворити в такий спосіб:
F2 = 3πV2d2Δ / Re. (2.33)
Турбулентний режим обтікання характерний для високих швидкостей руху (Re >1000) великих частинок (d > 2 мм). Турбулентне обтікання супроводжується утворенням вихрів за тілом, що рухається. Вихроутворення тим інтенсивніше, чим складніша конфігурація тіла і чим більша шорсткість його поверхні та швидкість обтікання. У результаті вихроутворення за тілом, що рухається, утворюється простір зі зниженим тиском. Різниця тисків визначає динамічний або інерційний опір середовища тілу, що рухається, який описується законом Ньютона-Ріттінґера:
F2•= πV2d2Δ / 16. (2.34)
Закони Стокса і Ньютона-Ріттінґера кожний окремо не відбивають повної картини опору середовища тілу, що рухається. Тіло випробує одночасно вплив двох опорів, але в різному ступені. При параметрах Рейнольдса Re <1 переважає дія сил в'язкості, при параметрах Рейнольдса Re >1000 – сил інерції.
Для проміжної області значень параметра Рейнольдса 1 ≤ Re ≤ 1000, що відповідають швидкостям руху частинок крупністю 0,1 ≤ d ≤ 2 мм, Аллен запропонував визначати опір тілу за формулою:
F2•=
5πV2d2Δ
/ (8
). (2.35)
Формули (2.33) - (2.35) показують, що опір середовища тілу залежить від густини середовища, швидкості руху і крупності тіла. При цьому коефіцієнт гідродинамічного опору середовища залежно від режиму руху набирає значення:
ψ = π / 16 – рух у турбулентному діапазоні;
ψ = 5π / (8 ) – рух у проміжному діапазоні;
ψ = 3π / Re – рух у ламінарному діапазоні.
У результаті узагальнення експериментальних даних Релеєм була отримана діаграма залежності коефіцієнта опору від параметра Рейнольдса ψ = f (Re) для різних режимів руху сферичних тіл у воді, повітрі, важких рідинах і т.п. (рис. 2.20). Плавний вигляд кривої вказує на поступовий перехід від ламінарного режиму до турбулентного при зміні параметра Рейнольдса.
ψ
104
103
102
101
100
10-1
Re
100
10-1
10-2
10-3
10-4
105
104
103
102
101
Рис. 2.20. – Залежність коефіцієнта ψ від параметра Re.
Для практичних цілей застосувати діаграму Релея досить складно, і, крім того, визначення, виконані з її використанням, не виключають похибок, як і при будь-якому іншому графічному методі.
Запропоновано багато рівнянь для опису різних ділянок кривої ψ = f(Re). Наприклад, для вільних умов падіння тіл і чисел Re < 6000 В.А.Олевським запропоноване рівняння:
ψ = 3π / Re + (3 / Re)0,5 + 1/8. (2.36)
При значеннях чисел Re > 6000 рівняння (2.36) дає занижені значення коефіцієнта опору ψ.
Аналітичне вираження для визначення швидкості руху тіла в середовищі може бути отримане з диференціального рівняння руху кулі:
. (2.37)
При m = πd3δ/6 для прискорення падаючого в середовищі тіла маємо:
,
м/с2. (2.38)
У перший момент часу тіло рухається в середовищі прискорено, тому що його сила ваги перевищує силу опору середовища. Цей момент часу малий і вимірюється частками секунди:
t0 = 2,5 V0 / g0, с, (2.39)
де t0 – час досягнення кінцевої швидкості руху, с; V0 – кінцева швидкість руху тіла, м/с; g0 – початкове прискорення, м/с2:
,
м/с2. (2.40)
За час t0 тіло проходить шлях L0:
L0 = 1,8 V02 / g0, м. (2.41)
Після закінчення проміжку часу t0 настає рівновага сил, і тіло рухається рівномірно зі швидкістю V0 = const, що називається кінцевою швидкістю вільного падіння. Прискорення тіла при V0 = const дорівнює нулю. З рівняння (2.38) кінцева швидкість падіння тіла в середовищі буде:
,
м/с. (2.42)
З урахуванням коефіцієнта опору ψ можуть бути отримані вирази для визначення швидкості руху тіл у різних режимах:
- турбулентному – ψ = π / 16:
,
м/с; (2.43)
- перехідному – ψ = 5π / (8 ):
,
м/с; (2.44)
- ламінарному – ψ = 3π / Re:
,
м/с. (2.45)
Аналіз формул (2.43) - (2.45) показує, що зміна температури рідини не позначиться на швидкості руху частинки в турбулентному режимі, слабко позначиться – у перехідному, але істотно – у ламінарному.
Вітчизняний вчений П.В.Лященко розробив універсальний метод визначення кінцевої швидкості руху тіл будь-якої крупності, густини і форми в різних режимах. На основі діаграми Релея була побудована в логарифмічних координатах діаграма Re2ψ = f(Re) (рис. 2.21).
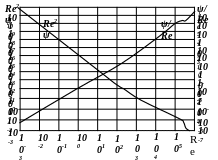
Рис. 2.21. – Залежність параметрів Re2ψ i ψ/Re від параметра Re .
Визначення кінцевої швидкості полягає в тому що при відомих параметрах частинки і середовища розраховується параметр Re2ψ :
Re2ψ = πd3(δ –Δ)gΔ / (6μ2). (2.46)
Потім за діаграмою (рис. 2.21) знаходять значення Re, після чого з використанням формули (2.31) визначають кінцеву швидкість:
V0 = Reμ / dΔ. (2.47)
При груповому (стисненому) русі мінеральних частинок різної густини і крупності завжди існує певна кількість частинок, які мають однакові швидкості руху в середовищі. Наприклад, частинка вугілля з параметрами δВ = 1500 кг/м3, dВ = 8 мм і частинка породи з параметрами δП = 1800 кг/м3, dП = 5 мм мають однакові швидкості руху.
Частинки, що при різній густині і крупності мають однакову кінцеву швидкість падіння в одному і тому ж середовищі, називаються рівнопадаючими, а відношення їхніх діаметрів – коефіцієнтом рівнопадіння е :
e = d1 / d2 =Re1 / Re2. (2.48)
де індекс «1» належить до частинок меншої густини, індекс «2» – до частинок більшої густини.
З умови рівності кінцевих швидкостей руху частинок коефіцієнт рівнопадіння може бути обчислений з використанням густини частинок і середовища:
e = [(δ2 - Δ) / (δ1 - Δ)]n. (2.49)
де n – показник ступеня, що залежить від режиму руху частинок; при русі в турбулентній області n = 1, у перехідній n = 2/3, у ламінарній n = 0,5.
За методом П.В.Лященка коефіцієнт рівнопадіння визначають з використанням параметра ψ/Re. Для частинки меншої густини параметр ψ/Re визначають за формулою:
ψ1/Re1 = πg(δ1 - Δ)μ / (6V03Δ2). (2.50)
Потім за діаграмою Re = f(ψ/Re) (рис. 2.21) знаходять число Рейнольдса для частинки меншої густини – Re1, з використанням якого визначають параметр ψ / Re для частинки більшої густини:
ψ2/Re2 = ψ1 (δ2 - Δ) / [Re1 (δ1 - Δ)], (2.51)
знаходять по діаграмі число Рейнольдса Re2 і визначають коефіцієнт рівнопадання за співвідношенням між числами Рейнольдса за формулою (2.31).