4. Пән бойынша тапсырмаларды орындау және өткізу кестесі

№	Жұмыс түрі	Тапсырма мақсаты мен мазмұны	Пайдалануға ұсынылған әдебиет	Бақылау түрі (рейтінгтік шкалаға сәйкес)	Балдар (рейтінгтік шкалаға сәйкес)	Сынақ түрі	Тапсыру уақыты
1	2	3	4	5	6	7	8
1	Коллок виум	Берілген материалдарды меңгеру және оны есеп шығаруда қолдану және практикалық тапсырмаларды орындау	Негізгі және қосымша әдебиеттер тізімі бойынша	Аралық бақылау	50-100	Ауыз ша	4 апта
	Бақылау жұмысы	Теориялық материалдардың бекітілуі	Негізгі және қосымша әдебиеттер тізімі бойынша	Аралық бақылау	50-100	Жазбаша	7 апта
	Есептік – графика лық жұмыстар	Әдебиеттерді дайындау, реферат жазу және тақырып бойынша сабақ айту	Өтіліп жатқан тақырып бойынша	Аралық бақылау	50-100	Ауыз ша	10 апта
	Белсенді лігі үшін	Студенттердің берілген материалдарды меңгеруін тексеру	Әдебиет тер тізім бойынша.	Аралық бақылау	50-100	Ауыз ша	15апта

. Пәннің оқу - әдістемелік картасымен қамтамасыз етілуі

№№	Курс бойынша оқулықтар мен оқу құралдарының атауы	КарМУ кітапханасын-дағы оқулықтар мен оқу құралдарының саны
	1.Негізгі әдебиеттер*
1	Тұрмұхамбетов А.Ж. Жылуалмасу негіздері. –А.: Рауан, 1995.	
2	Кабашев Р.А., Кадырбаев А.К., Кекильбаев А.М. Жылу техникасы – Алматы, Бастау, 2008 -425 б.	
3	Михеев М.А., Михеева И.М. Основы теплопередачи. –М.: Энергия, 1973.	
	Архаров А.М., Исаев С.И., Кожинов И.А. и др. Теплотехника.Учебник для ВУЗов./ Под ред. Крутова В.И. – М.: Машиностроение 1996 г.	
	Баскаков А.П.,Берг Б.В.,Витт О.К. и др. Теплотехника: Учебник для ВУЗов./Под ред.А.П.Баскакова.–М.: Энергоатом.,1991 г.	
	Шаров, Ю.И. Теплопередача через многослойную цилиндрическую стенку / Ю.И. Шаров. – Новосибирск: НГТУ. – 2001. – 18 с.	
	Шаров Ю.И. Техническая термодинамика и основы теплопередачи / Ю.И. Шаров, П.А. Щинников. – Новосибирск: НГТУ. – 2002. – 52 с.	
	Шаров, Ю.И. Теплопередача через оребренную стенку / Ю.И. Шаров, А.А. Ильиных. – Новосибирск: НГТУ.– 2005. – 16 с.	
	Шаров, Ю.И. Теплообмен при конденсации и кипении холодильного агента / Ю.И. Шаров, И.В. Бородихин.–Новосибирск: НГТУ. – 2004. – 23 с.	
	Теория тепломассообмена /Под ред. А.И. Леонтьева. - М.: Высшая школа, 1984.	
	Крейт Ф., Блэк У. Основы теплопередачи, Мир, 1983.	
	Кутателадзе, С.С. Основы теории теплообмена / С.С.Кутателадзе. – Новосибирск: Наука. – 1989. – 416 с.	
	Ташимов Л.Т. Конвективный тепло- и массообмен в пленочных процессах химической технологии /Вопросы моделирования и устойчивости. - Алматы: Бiлiм, 1999.	
	Исаченко В.П. и др. Теплопередача. –М.: Энергия, 1981.	
	2.Қосымша әдебиеттер**
	Карлсоу Х.С., Егер Д.К. Теплопроводность твердых тел. –М.: Наука, 1964.	
	Лыков А.В. Теория теплопроводности. –М.: Высшая школа, 1967.	
	Беляев Н.М., Рядно А.А. Методы теории теплопроводности. Высшая школа, М., 1982.	
	Исаченко В.П. Теплообмен при конденсации. –М.: Энергия, 1977.	
	Керташов Э.М. Аналитические методы в теплопроводности твердых тел. –М.: Высшая школа, 1979.	
	Тепло- и массообмен. Теплотехнический эксперимент: справочник / под ред. В.А. Григорьева. – М.: Энергоиздат. –1982. – 515 с.	
	Миснер А.В. Теплопроводность твердых тел, жидкостей, газов и их композиций. –М.: Мир, 1968.	
	Пехович А.И., Жидких В.М. Расчеты теплового режима твердых тел. Энергия, Л., 1978.	
23	Шорин С.Н. Теплопередача. –М.: Высшая школа, 1964.	
24	Рындин В.В. Методические указания к лабораторным работам. Часть 1.– Алма-Ата : НМК, 1992. – 67 с.	
25.	Краснощеков Е.А., Сукомел А.С. Задачник по теплопередаче: Учебное пособие – М.: Энергия, 1980 – 288 с.	
2	Практикум по теплопередаче / Солодов А.П., Цветков Ф.Ф., Елисеев А.В., Осипова В.А. – М.: Энергоатомиздат, 1986 – 296 с.	
27	Авчухов В.В., Паюсте Б.Я. Задачник по процессам тепломассообмена. Энергоиздат, 1986 г.	
28	Теплообменные аппараты ТЭС. Назмеев Ю.Г. Лавыгин В.М. 1998 г	
29	Тепло и массообменные аппараты ТЭС и АЭС. Ильченко О.Т. 1992 г	
30	Сборник задач_по технической термодинамике учебное пособие. Жуховицкий Д. Л. 2004 г.	
	2.1 Интернет көздері
	http://03-ts.ru,
	http://www.kodges.ru
	http://www.twirpx.com

 Лекциялық кешен (лекция тезисі)

№  дәріс. Кіріспе. Фурье заңы және оның стационарлы жылуөткізгіш есептерін шешуге арналған жуықтаулары

Жылумассаалмасу пәні мен әдісі: Жалпы жылумассаалмасу - жылуалмасу мен жылу берілу процесстері негізінде жүреді. Жылу берілу мен жылу алмасу дегеніміз қайтымсыз түрдегі кеңістікте және ортада өздігінен жылудың таралу процесін айтамыз. Мұндағы жылудың таралуы дегеніміз қарастыратын орта аймағымен және жеке элементтер арасындағы ішкі энергияның алмасуы болып табылады. Жылу берілу процесі үш әдіс бойынша беріледі:

1. Жылуөткізгіштік

2. Конвекция

3. Жылулық сәулелену

Жылуөткізгіштік: қарастыратын кеңістіктегі айнымалы температураға тәуелді. Денедегі немесе олардың арасындағы жылудың молекулалық берілуі.

Конвекция тек қана ағатын ортада болады. Конвективті жылу дегеніміз кеңістіктегі(ағатын орта) газ немесе сұйық көлемдерінің ауысуы кезіндегі олардың бір температуралы аймақтан басқа аймаққа берілу процестері. Бұл кезде жылудың берірлуі сұйық немесе газ ортадағы тасымалдау құбылыстарымен үзіліссіз байланыс та болады.

Жылулық сәулелену: тек қана шағылатын дененің оптикалық қасиеті мен температурасына негізделген. Электромагнит толқын көмегімен жылудың таралу процесі.

Температуралық өріс: Температуралы әртүрлі денелердің немесе денелерді құрайтын бөлшектер бір-бірімен жанасқанда жылу энергиясының таралу процесін жылуөткізгіштік деп атайды. Жылуөткізгіштік дененің микробөлшектерінің қозғалысына негізделген. Осы кездегі газдардағы энергияның тасымалдануы молекула мен атомдардың диффузиялық жолмен, ал сұйықтар мен қатты дене диэлектриктерде серпімді толқындар жолымен іске асады. Металдағы энергияның тасымалдануы еркін электродтардың диффузия құбылыстарымен жүзеге асады. Ал бұл жердегі кристалл торлардың серпімді толқынның міндеті екінші дәрежеде көрсетілген.

Бұл жерде айта кететін жайыт, сұйық пен газда жылуөткізгіштік таралуы конвекция процесі кезінде жүргізлуі мүмкін.

Жылуөткізгіштің аналитикалық зерттеуі кеңістікті, уақытты, температура өзгерісін оқуға негіздейді, яғни келесі теңдеу бойынша өрнектеледі:

(1.1)

Бірінші теңдеу температура өрісінің математикалық өрнегін көрсетеді. Сонымен, температура өрісі дегеніміз әрбір уақыт моменті үшін қарастырлатын кеңістіктің барлық нүктесіндегі температура мәндерінің жиынтығы. Стационарлы және стационарлы емес температура өрістері бар.

Бірінші теңдеу уақыт ағынына байланысты температура бір нүктеден басқа нүктеге өзгергендегі температура өрісірің кең таралған жалпыланған түрі болып табылады. Бұндай өріс жылуөткізгіштің орнықпаған жылулық тәртібі бойынша анықталады және стационарлы емес температураллық өріс деп аталады.

Егер жылулық тәртіп орныққан болатын болса, онда өрістің әрбір нүктесіндегі температура уақыт бойынша өзгеріссіз қалады және бұндай температуралық өріс стационарлы деп аталады.

Температура градиенті: Егер бірдей температураға ие дене нүктелерін қоссақ температуралары тең бетті аламыз және оны изотермиялық деп атайды.

Изотермиялық бет дегеніміз бірдей температураларға ие температуралық өрістегі нүктелердің геометриялық орны. Олар тек қана дене бетімен немесе толығымен дененің өзінің ішіне орнатылады.

Изотермиялық беттің қиылысуы тұтастықты береді. Бұл тұтастықта изотермал шоғыры орнатылған. Олар изотермиялық беттегі қасиеттерге ие, яғни олар қиылыспайды және дене ішінде шегі болмайды,тек қана бетте шектеледі немесе толығымен дененің өзінің ішінде орындалады.

1-суретте температуралары Δt ерекшелінетін издтермиялық бет көрсетілген. Денедегі температура тек қана изотермиялық бет қиылысатын бағытқа ғана бағытталады. Осы кезде бірлік ұзындықтағы көп мөлшерде температураның төмендеуі нормалдың изотермиялық бетке бағытында жүргізіледі .

Нормалдың изотермиялық бетке бағытындағы температураның өсуі температура градиентімен сипатталады.

1.1-сурет. Изотермиялық беттің бейнесі

Температура граденті және де, нормалдың изотермиялық беттің температура өсуі жағына бағытталатын вектор болып табылады. Және сан мәні осы бағыт бойнша туындысына тең, яғни келесі өрнекпен өрнектеледі.

(1.)

мұнда –нормалдың изотермиялық беттегі бірлік векторы және температураның өсу жағына бағытталады. - n нормал бойынша температура туындысы. - температура градиентінің скаляр шамасын изотермиялық беттің әртүрлі нүктесі үшін бірдей емес. Изотермиялық беттің арасындағы арақашықтық Δn кіші болған жерде ол үлкен болады.

Температура градиентінің скаляр шамасының бастапқыдай температура градиенті деп атайды.

Фурье заңы: Жылуды таратудың қажетті шарты қарастырылатын ортада темпператураның бірқалыпты емес түрде таралады. Сондықтанда, жылуды беру үшін дененің әртүрлі нүктесінде gradt ≠0 болмауы керек.

Фурье заңына сәйкес жылу мөлшері аралығында изотермиялық беттің элементі арқылы өтетін температура градиентіне тура пропорционал, яғни келесі өрнек бойынша анықталады:

(1.)

теңдеудегі пропорционалдық коэффиценіті заттың физикалық параметрі болып табылады. Бұл заттың жылуды өткізу қасиетін сипаттайды және жылу өткізгіштік коэффиценті деп атайды.

Бірлік уақыттағы бірлік изотермиялық бет ауданы арқылы өтетін жылудың мөлшері , Вт/м² жылу ағынның тығыздығы деп атайды. Бұл вектор және келесі қатынас бойынша анықталады.

(1.)

Жылыулық ағын тығыздығының векторы нормал бойынша изотермиялық бетке бағытталады. Оның оң бағыты температурасын кему бағытына сәйкес келеді.

Жылуөткізгіштік коэффиценті: Жылуөткізгіштік коэффиценті дегеніміз заттың физикалық параметрі болып табылады. Жалпы жағдайда жылуөткізгіштік коэффициенті заттың түріне, қысымына және температурасынан тәуелді.көп жағдайларда,әртүрлі материалдар үшін λ коэффициенті тәжірибе жүзінде анықталған және олар көптеген кітаптарда келтірлген. Оның ішіндегі көбісі берілген заттың температура градиенті мен жылулық ағынның өлшеміне негізделген.

Сендерге берілген 2-суретте әртүрлі заттың λ жылуөткізгіштік коэффициентінің мәндерінің реті көрсетілген.

Осы кезде λ коэффициенті λ [ ] келесі қатынас бойынша анықталады:

(1.)

1.2-сурет. Әртүрлі заттың жылуөткізгіштік коэффициенті

(1.) теңдеуден көретінімз, λ коэффициенті кездегі бірлік аралығында бірлік изотермиялық бет арқылы өтетін жылудың мөлшеріне тең.

Біздің білумізше, дене әртүрлі температураға тәуелді, ол жылуалмасу кезінде дененің өзінде температура тепе теңсіздік жағдайында таралады. Онда біз бірінші орында жылуөткізгіштік λ коэффициентінің температурадан тәуелділігін біліуміз қажет. Тәжірибеде көрсетілгендей, көптеген материалдарда λ коэффициентінің температурадан тәуелділігі сызықты болып қалыптасқан:

(1.11)

мұндағы — температура кезиндегі жылуөткізгіштік коэффициенті; — тәжірибе түрінде анықталатын, тұрақты.

Негізгі әдебиеттер: 1 – 4

Қосымша әдебиеттер: 1-2.

№  дәріс. Жылуөткізгіштік есебінің математикалық формировкасы

Жылуөткізгіштің дифференциалдық теңдеуі біртекті және изотропты дененің ішінен көлемі , ал қырлары тең элеменіттар параллепипедті бөліп аламыз. (.-сурет), дененің физикалық қасиеттері (тығыздығы , жылусыйымдылығы С, және жылуөткізгіштік коэффициенті λ) параллепипедтің кез келген нүктелерінде бірдей және уақыт өткен сайын өзгермейді. Сол жақтағы қырдың температурасы , ал қарама қарсы қырдың температурасы тең. .-суретте жылуөткізгіштіктің дифференциалдық теңдеуін қортып шығаруға арналған элементар параллелепипедтің көрінісі көрсетілген.

2.1-сурет. Жылуөткізгіштіктің дифференциальдық теңдеуін қорытуға арналған параллелепипедтің бейнесі

Біріншіден, уақыт аралығында параллепипедтің осьтеріне байланысты барлық қырлары арқылы енетін жылудың мөлшерлерін анықтаймыз, содан кейін параллепипедтің қарама қарсы қабырғаларынан шығарылатын жылудың мөлшерін анықтаймыз. Осы есептеулердің негізінде параллепипедтің ішінде қалған жылудың мөлшері келесі өрнекте көрсетіледі:

(2.)

Энергияның сақталу заңы бойынша параллелепипедтегі жылу мөлшерінің өсімшесі параллепипед энергиясының өзгеруіне тең, яғни:

(2.)

мұнда - уақыт аралығындағы параллелепипед температурасының өзгеруін сипаттайды. (2.) және (2.) өрнектерін теңестіреміз:

(2.)

Бұл өрнектен уақыт моментіне байланысты параллелепипедтің ішіндегі температураның өзгерісін анықтаймыз, яғни ол келесі түрде жазылады:

(2.)

мұндағы белгілейміз онда (2.) теңдеуі келесі түрде жазылады:

(2.)

мұндағы температураөткізгіштік коэффициент.

Бұл теңдеу дененің кез келген нүктесіндегі температураны анықтайды және бұл теңдеуді қозғалмайтын ортадағы жылуөткізгіштіктің дифференциалдық теңдеуі деп атаймыз.

Температура өткізгіштік коэффициент дененің жылу инерциялдық қасиетін сипаттайды. Температура өткізгіштік коэффициенті жоғары денені температура өткізгіштік коэффициенті төмен денемен жанастырған жағдайда бірнеше дене тез қызады немесе тез салқындайды, себебі температурасы төмен дене жоғары температуралы денеден жылуды алып қызу немесе жоғары температуралы дене төменгі температуралы денеге жылуды беріп сууы мүмкін. Стационар жылуөткізгіштік процесін қарастырамыз, яғни (уақыт өскен сайын температура өзгермейді), онда (2.) теңдеу келесі түрде жазылады:

(2.)

мәні нөлге тең болуы мүмкін емес, сондықтан

(2.)

немесе

Бұл теңдік стационар жылу режиміне арналған қозғалмайтын ортадағы жылуөткізгіштік теңдеуі және ол жылу энергиясынның берілуі кезінде температураның таралуын сипаттайды. Нақты жағдайды қарастырғанда осы теңдеулер геометриялық факторларды есепке алатын шекаралық шарттармен толықтылуы қажет.

Жалпы жағдайда, жылуөткізгіштік теориясы феномонологиялық теория болып табылады, сондықтанда ол жылудың таралу процесінің механизмін қарастырмайды, тек қана осы процесті энергияның сақталу немесе Фурье заңдары негізінде сипатталуымен шектеледі.

Қатты дене үшін энергияның дифференциалдық теңдеуі келесі түрде болады:

(2.)

Егер денеде жылу көзі болмайтын болса , онда Фурьенің дифференциалдық теңдеуімен қанағаттандырылады.

(2.)

Стационарлы жылуөткізгіштік кезінде және Лаплас теңдеуімен қанағаттандырылуы керек:

(2.1)

Стационарлы жылулық режимі және ішкі жылу көзі бар кездегі температура өрісі Пуассон теңдеуімен сипатталады:

(2.1)

Бірмәнділік шарттары: Бірмәнділік шарттар дегеніміз – нақты есептің өзіндік ерекшеліктері. Бірмәнділік шарттар төрт топқа бөлінеді: геометриялық, физикалық, уақыттық немесе бастапқы, және шекаралық немесе беттік.

Геометриялық шартта қарастырып отырған ортаның (дененің) геометриялық пішіні мен өлшемі жатады. Дененің геометриялық пішінін ескерсек соған сәйкес арнаулы координаталық жүйедегі цилиндрлік, сфералық таңдай отырып дененің симметриясын ескеріп дифференциалдық теңдеуді әжептәуір қарапайым түрге келтіруге болады.

Физикалық шартта ортаның физикалық қасиеттері мысалы: тығыздық, тұтқырлық, жылу сиымдылығы, жылуөткізгіштік және ішкі жылу көздерінің орналасу шарттары жатады. Физикалық қасиетті ескеру арқасында дифференциалдық теңдеуді қарапайым түрге келтіруге болады.

Уақыттық немесе бастапқы шарттар стационар емес есептерді шешу үшін қажет. Бұл шарттар бастапқы уақыт мезгілінде денедегі температураның таралу заңдылығын анықтайды, яғни бастапқы уақыт мезетінде денедегі температуралық өріс беріледі.

Шекаралық немесе беттік шарттың өзі төртке бөлінеді:

1) I тектік шекаралық (беттік) шарт. Әрбір уақыт мезгілінде дене бетіндегі температураның таралуы беріледі.

2) ІІ текті шекаралық шарт кез-келген уақыт кезеңі үшін дене бетінің әрбір нүктесіндегі жылу ағыны тығыздығының шамасын бейнелейді.

3) ІІІ текті шарт бойынша орта мен дене бетінің арасындағы жылу алмасу заңы мен ортаның температурасы беріледі. Мысалы: Қызған дене газ немесе сұйық ортаға қойылсын. Жылу ағыны дене бетінен шығып ортаға тарайды. Орта мен дене беті арасындағы жылу ағыны болады. Жылу алмасу заңы ретінде төмендегі Ньютон-Рихман теңдеуі қолданылады:

(2.2)

мұнда – қызған бет температурасы, – орта температурасы.  – жылу беру коэффициенті. Оның өлшем бірлігі Вт/м²К.

Жылу беру коэффициенті көп факторларға: дене бетінің күйіне, ортаның физикалық қасиеттеріне, ағынның жылдамдығына және т.б. тәуелді, яғни ол физикалық емес, айнымалы шама. Дене бетінен ортаға жылу берілгеннен кейінгі ішкі қабырғасы дене ішіндегі жылу алмасу Фурье заңына байланысты, яғни процесс тұрақты ішкі қабырғадан сыртқы бетке қанша жылу берілсе, сонша жылу сыртқы ортаға шығарылады.

(2.3)

(2.4)

4) IV текті беттік шарт денелер жүйесінің немесе дененің ортамен жылуөткізгіштік арқылы жылуалмасуын сипаттайды және осындай шартта денелер өзара идеал түйісіп тұрған кезде қарапайым түрде беріледі. IV текті беттік шарт көптеген техникалық қондырғыларда көп қабатты орамды материалдарда жылудың таралуын анықтау үшін қолданылады. Яғни, бір қабаттың жылуөткізгіштігі кіші, екіншісінікі орташа, үшінші қабаттың механикалық беріктігі жоғары болуы мүмкін. Мысалы: термостатты қарастырғанда, біз түйіскен қабаттың арасындағы жылуөткізгіштікті қолданамыз. Осы кезде IV текті беттік шарттың түйісу бетінің арасында қуыстар немесе басқа да бір бөгде заттар болуы мүмкін.

(2.5)

IV текті беттік шарттар.

Негізгі әдебиеттер: 1 – 4.

Қосымша әдебиеттер: 1-2.

№  дәріс. Ішкі жылу көзі бар стационарлы жылуөткізгіштік есептерін шешу. Стационарлы емес жылуөткізгіштіктің негізгі теориялары

Шексіз жазық дененің жылу өткізгіштігі (ішкі жылу көзі жоқ кездегі жылуөткізгіштік): Бір текті, изотропты, жылу физикалық қасиеттері тұрақты жазық дененің жылуөткізгіштігін зерттейік. Пластина OZ, OY бағыттарында шексіз, ОХ бағытында қалыңдығы , ішкі жылу көздері жоқ болсын (3.1- сурет).

OZ, OY бағыттарында пластина шексіз болуы себепті, бұл бағыттардағы температура өрісінің өзгеруін қарастырмауға болады. Олай болса Лаплас теңдеуі тіпті қарапайым түрге келеді.

(3.1)

3.1-сурет. I – текті беттік шарт кезіндегі шексіз пластинаның стационар жылуөткізгіштігі

Iші текті беттік шартты келесі түрде жазуға болады:

(3.2)

(3.1) теңдеуді екі рет интегралдап, (3.2) шарттарды қолдансақ температура өзгеруін өрнектейтін мына сызықтық шешімді жеңіл алуға болады.

(3.3)

Бұл шешімді қолдануға қолайлы өлшемсіз түрге келтірейік. Ол үшін қарастырылған процеске мынадай шамаларды енгіземіз: –толық температуралық айырым; –айнымалы температуралық айырым. Осы шамаларды жоғарыдағы өрнекке қоя отырып, теңдеуді өлшемсіз түрге келтіреміз: , мұндағы өлшемсіз температура, өлшемсіз координата.

Жылу ағынын есептеу үшін Фурье заңын қолданып, температура градиенті (3.3) теңдеуін өндейміз:

(3.4)

Олай болса

(3.5)

немесе

(3.5*)

мұндағы: –қабырғаның жылуөткізу қабілеті; ал -жылулық немесе термикалық кедергі; –жылу ағыны кеміп өткен беттің ауданы.

(3.5) формуланы қолдана отырып айнымалы температураны жылу ағынының тығыздығы арқылы есептейік. Енді жылуөткізгіштік температураға тәуелді деп қарастырайық. Олай болса Фурье заңы мына түрге келеді.

(3.6)

Әріқарай (3.6) теңдеуін О-ден Х-ке дейін және -ден -ге дейін интегралдасак, температураның төменгі мәнін табамыз:

(3.7)

Егер қарастыруға жылуөткізгіштіктің мына орташа мәнін енгізсек.

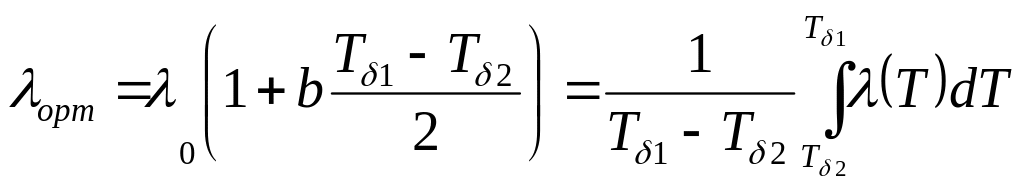(3.8)

Онда шешім төмендегідей болады.

(3.9)

Көп қабатты қабырғаның жылуөткізгіштігі. Қабырға бір текті қалыңдықтағы әр түрлі қабаттан құралған дейік (3.2-сурет), қабаттар өзара идеал түйісіп тұрғандықтан, түйісу беттеріндегі температуралар бір-біріне тең. Жылу тек бір бағытта таралады және қабаттардың жылу өткізгіштігі тұрақты деп үйғарсақ, кез келген изотермиялық бет арқылы өткен жылу ағынының тығыздығы да тұрақты болады.

3.2-сурет. Көп қабатты қабырға

Олай болса, әр қабат арқылы өтетін жылу мөлшерінің теңдеуін жазып, оларды өзара теңестіреміз. Осы теңдеулерден температура айырымын анықтап, алынған формулалардың оң жақтарын және сол жақтарын мүшелеп қоссақ, жылу ағынының тығыздығы үшін мынадай өрнек аламыз:

(3.1)

Инженерлік есептеулер үшін эквиваленттік жылуөткізгіштік деген шама енгізген қолайлы.

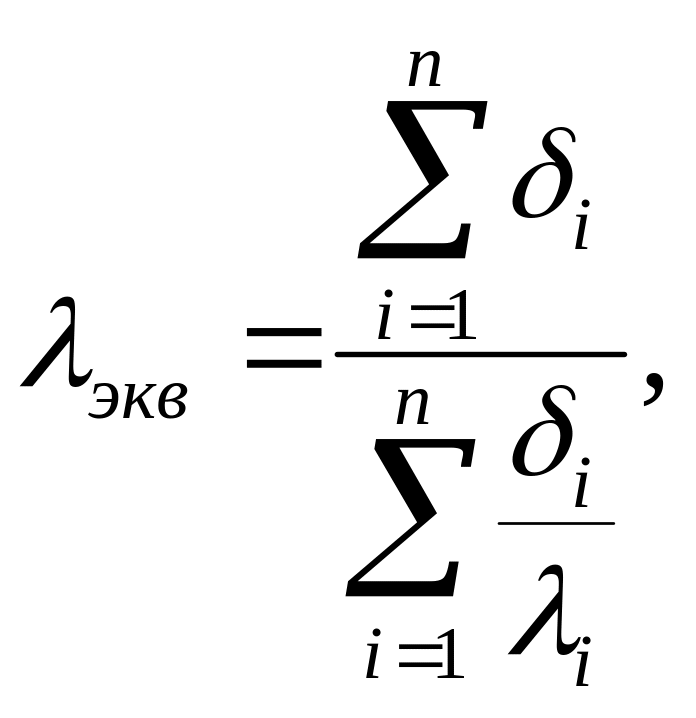(3.1)

Онда (3.1) мына түрде келеді.

(3.1)

мұндағы - көп қабатты қабырғаның қалыңдығы.

Шексіз жазық дененің жылуөткізгіштігі (ішкі жылу көзі бар кездегі жылуөткізгіштік): Енді стационap жылуөткізгіштікті ішкі жылу көздері бар кезде қарастырайық, қуаты тұрақты ішкі жылу көздері бір қалыпты орналасқан болсын (егер олар бірқалыпты орналаспаса, онда қабырғаны жылу көздері бірқалыпты орналасқан бірнеше қабаттарға бөлуге болар еді). Осы баптың басында айтылған қосымша шарттар орындалатын болса, онда жылуөткізгіштіктің дифференциалдық теңдеуі мына түрге келеді.

(3.1)

Беттік шарттар (3.2) түрінде болады және (3.1) теңдеуді екі рет интегралдау нәтижесінде мынадай жалпы шешім аламыз.

(3.1)

Беттік шарттарды қолдана отырып тұрақтылардың мәндерін есептеп, жалпы шешімге қойсақ, температураның таралуын мына тендеу өрнектейді.

(3.1)

Алынған шешімді (3.3) теңдеумен салыстырсақ ішкі жылу көздерінің бар болуы салдарынан, шешімде қосымша үшінші мүшенің пайда болғанын көреміз. Яғни, температура таралуы бұрынғыдай түзу сызықты емес, дөңес (жылу шығару көздері), немесе ойыс (жылу жұту көздері) болады. (3.1) шешімді бұрынғыдай өлшемсіз түрде жазуға болады (3.3-сурет, b қисығы):

3.3- сурет. ІІІ текті беттік шарт бар шексіз пластинаның стационар жылуөткізгіштігі

(3.1)

Әрі қарай шексіз пластинаның стационар жылу өткізгіштігін үшінші текті беттік шарттар орындалғанда зерттейік (3.3-сурет)

Бұрынғыдай қалыңдығы , жылулық физикалық қасиеттері тұрақты пластина ОУ және 0Z бағыттарында шексіз. Жылу сол жақтағы ортадан ОХ бағытында оң жаққа жазық қабырға арқылы өтеді. Жылу беру коэффициенттері тұрақты және есептің шарты бойынша белгілі. Үшінші текті беттік шартқа сәйкес, алдымен бірінші ортадан сол жақ бетке берілген жылу ағынының тығыздығы, одан кейін оң беттен екінші ортаға берілетін жылу шамасы, сонында аралық қабырға арқылы өтетін жылуың мөлшері жылуөткізгіштік теңдеуі негізінде анықталады.

Жылуды шығару немесе жұту көздері болмағандықтан, алынған жылу мөлшерінің теңдеулерінің сол жағындағы мүшелер бірдей. Осы жағдайды ескерсек, мына есептеу формуласын жеңіл алуға болады.

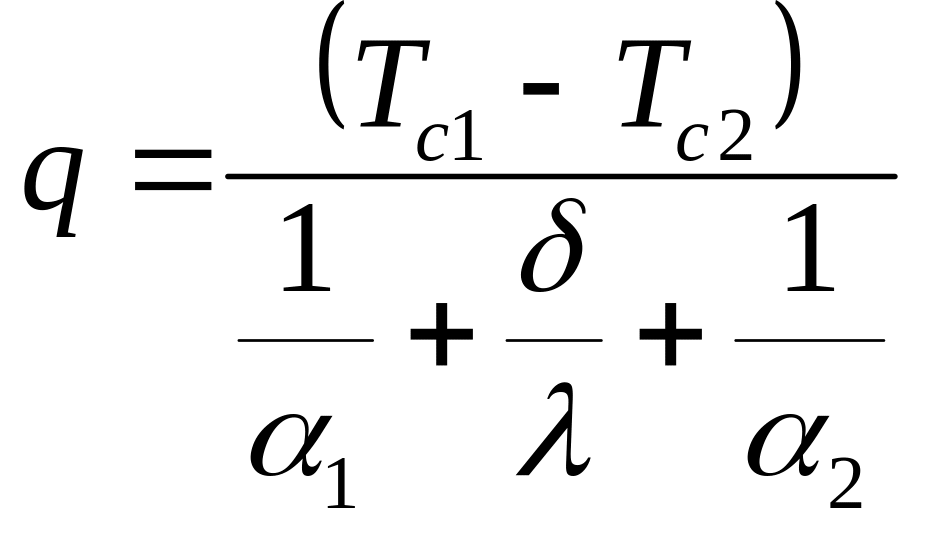(3.)

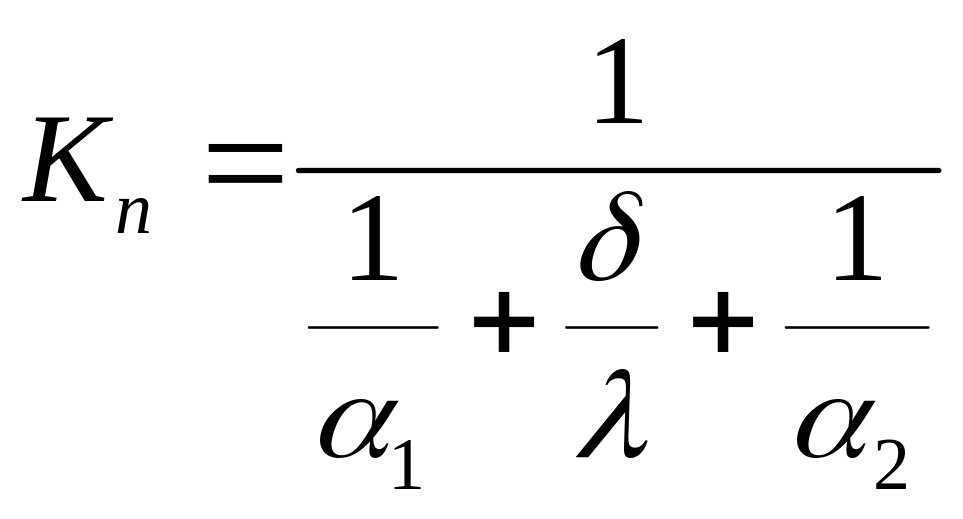мұндағы - жылуберілу коэффициенті деп және оған кері шама жылулық немесе термикалық кедергі деп аталады. Көп қабатты қабырғаның термикалық кедергісі келесі түрде жазылады:

(3.)

(3.5) және (3.22) шешімдерді салыстырсақ, І текті беттік шарт үшін алынған шешім ІІІ текті беттік шарт үшін алынған шешімнің жылу беру коэффициенттерінің шексізге ұмтылған кездегі дербес түрі екенін байқаймыз.

Шексіз ұзын цилиндр қабырғаның жылуөткізгіштігі: OZ бағытында ұзындығы шексіз біртекті цилиндрлік кабырғаның стационар жылу өткізгіштігін қарастырайық. Температураның таралуы бірінші текті беттік шарттар орындалғанда, ішкі жылу көздері жоқ болғанда есептелсін. Дененің жылу физикалық қасиеттері тұрақты деп санайық. Айтылған шарттар орындалғанда цилиндрлік координаталар жүйесінде температураның таралу симметриясын ескерсек,

(3.)

Бұл теңдеуді мынадай беттік шарттарды қолдана отырып шешуіміз керек (3.4-сурет). болғанда , болғанда . жаңа айнымалы шама енгізсек, онда (3.) теңдеуі жеңіл интегралданады: . Енді жоғарыдағы шарттарды қолдана отырып және тұрақтыларын табайық. Егер болса, Егер болса, . Бұдан ; 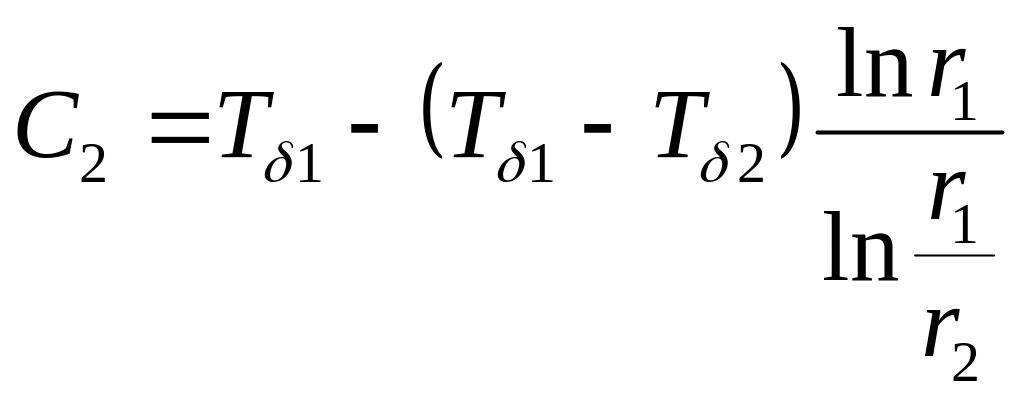. Бұл мәндерді (3.)–ге қойып, түпкілікті мына нәтижеге келеміз

(3.)

немесе оның өлшемсіз түрі келесі өрнекте корсетілген.

(3.*)

3.4-сурет. Шексіз ұзын цилиндр қабырғаның жылу өткізгіштігі

Алынған шешімге қарағанда цилиндрлік қабырғада температура логарифмдік заңдылықпен өзгереді екен. Мұның себебі, коаксиалды изотермиялық бір беттен екінші бетке өткенде температура градиентінің тұрақты болмауында. Яғни, жылу ағынының тығыздығы изотермиялық беттердің ауданы тұрақты болмағандықтан цилиндрлік беттердің радиусына тәуелді.

Бірлік уақыт аралығындағы жылу ағынын есептеу үшін белгілі Фурье заңын қолданамыз

(3.0)

мұнда , ал -ді табу үшін жоғарыдағы шешімді қолдануға болады: олай болса,

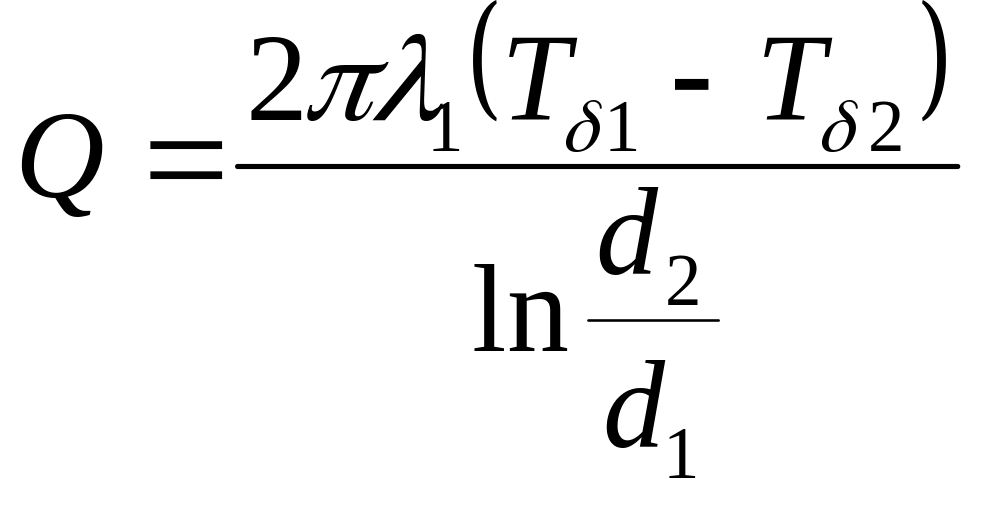(3.1)

Керісінше, инженерлік есептерде жиі кездесетін шама - жылу ағынының тығыздығы жоғарыда айтылғандай цилиндрлік беттің радиусына тәуелді. Әдетте, жылу ағынының тығыздығын (3.1) - ды қолдана отырып үш түрлі әдіспен есептейміз, яғни бірінші, ішкі беттің бірлік ауданы үшін; екінші, сыртқы беттің бірлік ауданы үшін; үшінші, цилиндрлік беттің бірлік ұзындығы үшін. Соңғы есептелген теңдеудің өлшемі Вт/м шаманы жылу ағынының сызықтық тығыздығы деп атайды. Оларды есептегеннен сон сол формулалардан тығыздықтардың арасындағы қатынастарды теңестіріп аламыз. Одан кейін, енді үшінші текті беттік шартқа сәйкес цилиндрлік қабырға арқылы жылу өту процесін қарастырайық, қарастырылып отырған бір текті цилиндрлік қабырғаның жылуөткізгіштігі , ішкі және сыртқы беттерінің жылу беру коэффициенттері тұрақты. Оған қоса ішкі және сыртқы орталардың Т_с1, Т_с2 тұрақты температуралары берілген (3.4-сурет). Егер құбырдың ұзындығы диаметрінен анағұрлым ұзын деп алып, OZ бағытындағы температура өзгеруін ескермей жылу ағыны ыстық ортадан құбыр бетіне беріледі, әрі қарай жылуөткізгіштік арқылы екінші бетіне тасымалданып, одан суық ортаға беріледі деп қарастыруға болады. Анық болу үшін ішкі орта ыстық деп болжайық (Т_с1 >Т_с2). Олай болса, цилиндрлік қабырғаның бірлік ұзындығы үшін әрбір қабырғалардың ұзындықтары бойынша өтетін жылудың ағындарын анықтайтын теңдеулерді жазамыз. Бұл формулалардан температура айырымдарын анықтап, алынған теңдеулерді мүшелеп қоссақ, сонғы қорытынды теңдеуді алып Ньютон-Рихман тендеуінің формасын қойып жылу беру коэфициентін анықтаймыз:

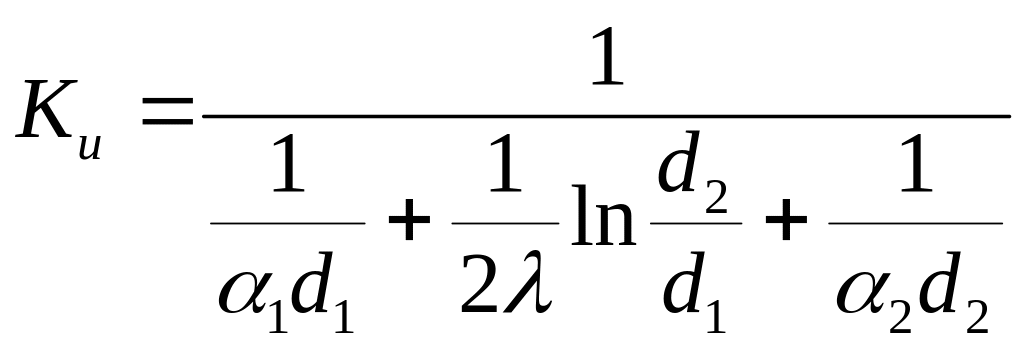(3.)

мұнда - цилиндрлік қабырғаға үшін жылу өтудің сызықтық коэфициенті, . температура айырымы градус екі ортаны бөліп тұрған ұзындығы 1 м цилиндрлік қабырға арқылы уақыттын бір өлшемінде өткен жылу ағынының мөлшерін көрсетеді.

Негізгі әдебиеттер: 1 – 4.

Қосымша әдебиеттер: 1-2.

№ 4 дәріс. Жылу берілудің негізгі теориялары. Жылуалмастырғыштардың жылулық есептеулері

Жылу беру теориясы жылу энергиясын тікелей, технологиялық пайдалану үрдістерін үйретеді жєне жылуды бір денелерден басқаларға тасымалдау құбылыстарының кешенін, сондай-ақ берілген дененің бөлшектері арасындағы жылудың берілуін қамтиды. Басқаша айтқанда жылу беру жылудың таралу үрдістері туралы оқу болып табылады.

Цилиндрлік қабырғаның критикалық диаметрі: Біртекті цилиндірлі қабырғаның диаметрінің өзгерісі термиялық кедергіге қалай әсер ететінін қарастырайық.

(4.1)

және мәндері тұрақты болғанда цилиндірлі қабырғаның жылуберілуінің термиялық кедергісі сыртқы диаметрге тәуелді.

Жылуөткізгіштің термиялық кедергісі диаметрі ұлғайған сайын өседі, ал жылу берілудің термиялық кедергісі кемиді. R_lc мен R_l2- нің қосындысы толық термиялық кедргінің мәніні береді.

Re-дің цилиндірлі қабырғаның қалыңдығына байланысты қалай өзгеретінін байқау үшін Re-ді d₂ функциясы ретінде қарастырамыз. Re-дің d₂-ның туындыларын 0-ге теңестіреміз.

(4.2)

Соңғы өрнектегі d₂-ның мәні қисығының экстремальді нүктесіне сәйкес келеді. Берілген қисықтағы нүктені максимум мен минимумға анықтау барысында экстремальді нүктенің минимум екенін байқаймыз. мәні кезінде жылу берілуінің термиялық кедергісі минимум болады. Жылу берілудің минималды термиялық кедергісіне сәйкес келетін құбырдың сыртқы диаметрі критикалық диаметр деп аталады және былай белгіленеді d_кр. Критикалық диаметр мына формула бойынша анықталады:

(4.3)

Егер d₂<d_кр болса, онда жылу берілудің термиялық кедергісі төмендейді, сыртқы диаметр термиялық кедергіге әсер етеді.

Егер d₂>d_кр болса, онда термиялық кедергі жоғарылайды. Бұл қарастырылған шарттар кезінде цилиндрлік аппараттарды және құбырларды жылулық оқшауланған деп есептейміз. Оқшауланған құбырлардың критикалық диаметрін қарастырайық. Мұндай құбыр үшін термиялық кедергі былай жазылады:

(4.4)

теңдігінен көрінетіні сыртқы оқшауланған d₃ диаметрі ұлғайғанда q_l жоғарылайды және d₃=d_кр болғанда q_l максимумға дейін жетеді. Ал, сыртқы диаметр ұлғайған сайын q_l төмендейді. Цилиндрдің бетін жабуға арналған жылудан оқшауланған материалды алу үшін оның алдымен критикалық диаметрін табу керек. Егер d_кр d₂-ге қарағанда үлкен болса, онда таңдалған материал жарамсыз.

Таңдалған материал жылу оқшаулағыш ретінде дұрыс жұмыс істеуі үшін d_кр<d₂ болу керек. Мысалы: сыртқы диаметрі d=20мм құбырды жылу оқшаулағыш материалмен қаптау керек. Оқшаулағыш ретінде жылуөткізгіштігі , ал жылу берілу коэффициенті d₂=5Вт/м²К болатын асбест алынады. Алдымен асбесттің критикалық диаметрін есептейміз.

Оқшаулағыштың критикалық диаметрі

мм

d₂>d_кр болғандықтан, асбестті жылу оқшаулағыш материалы ретінде қолдануға келмейді.

Бұл тақырыптағы қарастырылған критикалық диаметр дөңгелек цилиндрге байланысты қарастырылады.

Жылу берілудің пәрменділігін арттыру жолы: а) жылу берілудің интенсификациясын жылу берілу коэффициентін жоғарлату жолымен қарастыру.

Жылу берілу өрнегінен

(4.5)

байқайтынымыз берілген қабырғаның өлшемі мен сұйықтың температурасын анықтайтын жылу берілуі к болып табылады.

Жылу берілу - бұл күрделі құбылыс. Оның дәл мәнін анықтау үшін жеке-жеке бөліктеріне талдау жасау керек.

Мысалы біз жазық қабырға үшін қарастырсақ, онда:

(4.6)

Егер ұмтылса, онда

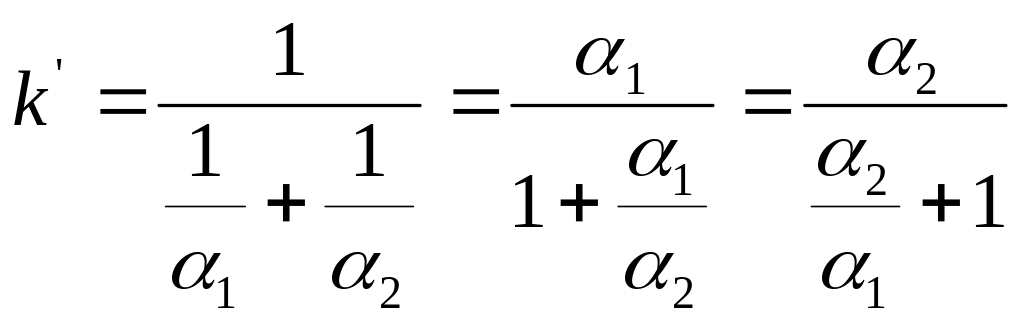(4.7)

Егер болса, онда k^’ -ның шекті мәніне ұмтылады.

Егер болса, онда жылу берілу коэффициенті -ге ұмтылады.

б) жылу берілу интенсификациясын қабырғаның көмегімен анықтау. Цилиндр қабырғасы арқылы берілетін жылу термиялық кедергілермен ғана анықталып қоймайды, сонымен қатар беттің өлшемдерімен де анықталады. d₁ және d₂ диаметрлері және өрнегіне сәйкес шар қабырғасы арқылы өтетін жылуға қатты әсер етеді. Бұдан байқалатыны термиялық кедергіні азайту үшін беттің ауданын ұлғайту керек. Қабырға арқылы жылу берілсе термиялық кедергі келесідей түрленеді:

және (4.8)

Қабырғадағы жылудың берілуі аналитикалық шешімдерге қатысты күрделі. Алдыңғы тақырыптарда қарапайым геометриялық денедегі жылуөткізгіштікті қарастыратын боламыз.

Жазық қырлы қабырғадағы жылу берілу: Шексіз өлшемі бар жазық қырлы қабырғадан ағып өтетін жылу ағынды анықтайық.

Жазық қырлы қабырғадағы жылу берілу коэффициенті тұрақты. Сонымен қатар қырлардың геометриялық өлшемдері мен жылу тасушылардың температуралары берілген.

>> қыры үшін периметр u=2в-ға тең. Қырдың көлденең қимасының ауданы F=в

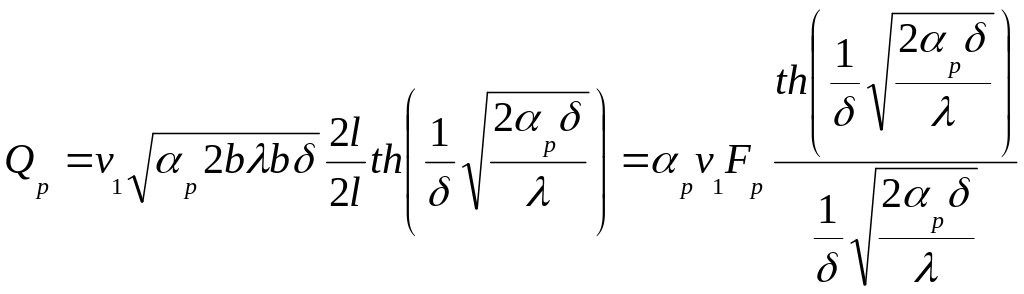(4.9)

мұндағы -био саны. Био саны жылуөткізгіштік процесін сипаттайды. Сыртқы термиялық кедергі үшін Био саны былай анықталады:

Bi= (4.10)

Қырдың бетімен таралатын жылу ағынның қорытынды теңдеуін былай жазамыз:

(4.11)

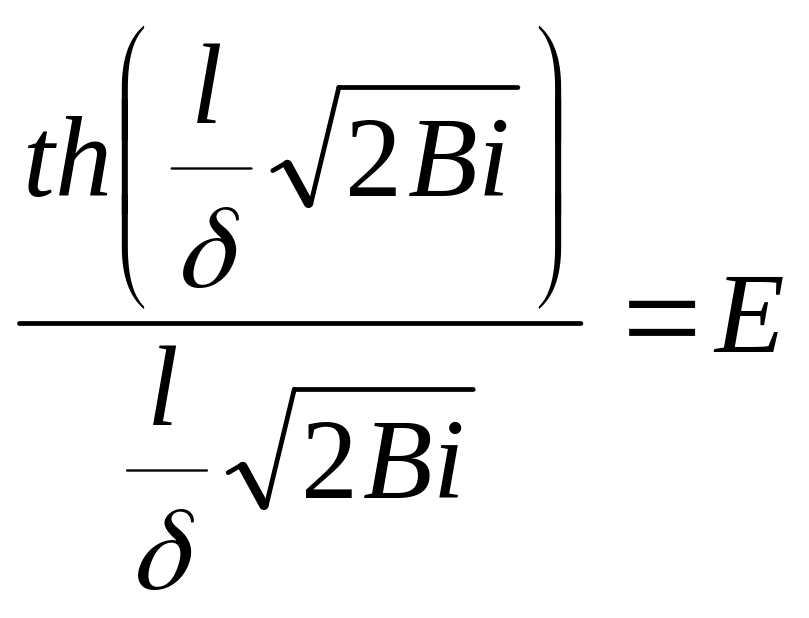деп белгілейміз.

Негізгі әдебиеттер: 1 – 4.

Қосымша әдебиеттер: 1-2.

№ 5 дәріс. Конвективті жылуалмасу теориясының жалпы ұғымы. Біртекті ортадағы конвективті жылуалмасудың теоретикалық негізі

Конвективті жылуалмасу газдар мен сұйықтардың қозғалысы кезінде болады. Бұл кезде жылу тасымалдану конвекция мен жылуөткізігіштік арақылы жүзеге асады. Конвекция тек ағатын ортада болады. Бірлік уақыт аралығында бірлік аудан арқылы жылудын таралуы.

(5.1)

мұндағы -сұйықтың тығыздығы

Газ немесе сұйық қозғаласы кезінде температуралары әр түрлі дене бөлшектері бір-бірімен жанасады, сол кездегі конвективті жылуалмасу мына теңдік бойынша жазылады:

(5.2)

Сұйық немесе газ ағынның дене бетімен конвективті жылуалмасуы конвективті жылу берілу немесе жылу берілу деп аталады. Жылу берілуді есептеу үшін Ньютон-Рихман заңын қолданамыз:

(5.3)

Ньютон-Рихман заңы бойынша жылу ағыны дене бетінің ауданына және температура өзгерісіне тура пропорционал. (5.3) теңдеуіне сәйкес жылу беру α былай есептеледі:

(5.4)

Жылу берілу коэффициенті дененің пішініне, өлшеміне қозғалыс режиміне, сұйықтың немесе газдың температурасына және жылдамдығына тәуелді. Сұйықты қозғалысқа келтіру үшін қандай да бір күш жұмсау керек.Сұйыққа әсер ететін күштер екіге бөлінеді. Оларға келесілер жатады: 1) беттік күштер : 2) көлемдік күштер- . Конвекцияның ерікті және еріксіз түрі болады. Ерікті конвекция біртексіз температура өрісінен пайда болады, ал еріксіз конвекция беттік күштердің немесе көлемдік күштердің әсерінен пайда болады.

Конвективті жылуалмасудың дифференциалдық теңдеуі: Аналитикалық түрде температура өрісін, жылдамдықты және жылу ағынның тығыздығын анықтау үшін келесі теңдеулерді қолданамыз.

Энергия теңдеуі: Қозғалыстағы сұйықтың температура өрісінің дифференциалдық теңдеуін шығарайық. Бұл кезде сұйықты біртекті және изиотропты деп есептейміз. Алдымен қырлары параллелипипедті қарастырамыз. Оның қырлары арқылы жылудың берілуі жылуөткізгіштік және конвекция арқылы жүзеге асады.

Бұл теңдеу қозғалыстағы сұйықтың температурасының таралуының энергиясының теңдеуі.

Қозғалыс теңдеуі. Қозғалыс теңдеуі Ньютонның екінші заңынан шығарылады. Жалпы жағдайда сығылмайтын сұйықтың қозғалыс теңдеуі үш теңдікпен сипатталады. Бұл үш теңдік осьтеріне қатысты. Мысалы осі бағытындағы қозғалыс мөлшері келесі теңдеу бойынша анықталады:

(5.7)

Жоғарыдағы теңдеуге сәйкес осі мен осі үшінде қозғалыс мөлшерін жазамыз. Осы теңдеулер Навье-Стокс теңдеулері деп аталады

Келесі қарастыратын теңдеу тұтас орта теңдеуі. Бұл теңдеу массаның сақтауына негізделген. Тұтас орта немесе үзіліссіздік теңдеуі былай анықталады.

(5.)

Егер сығылмайтын сұйықтар үшін болса, онда теңдеу келесідей түрленеді:

(5.)

Энергия теңдеуінің құрылымы. Оны талдау: Қарапайым көлемдегі қозғалатын орта үшін термодинамиканың бірінші бастамасын мына түрде жазуға болады:

(5.1)

мұндағы: - бірлік уақытта бірлік көлемдегі жылу мөлшері, Вт/м³; - бірлік уақытта бірлік көлемде ішкі күштермен жасалған жұмыс, Вт/м³. Термодинамика заңдарынан белгілі:

(5.1)

мұндағы: -қысым,Па, -меншікті көлем,м³/кг. Ендеше

(5.1)

-ны анықтау үшін қарастырылып отырған ортадан шектелген беттегі шеткі көлемді бліп аламыз.Бұл көлемнің бірлік уақытқа тең жылулық тепе-теңдігінің теңдеуін мына түрде жазуға болады:

(5.1)

мұндағы: - жылудың ішкі көздерінің интенсивтілігі, Вт/м³.

Гаусс-Остраградский теңдеуі мен тұтас орта жуықтауларын қолдана отырып,мынаны аламыз:

(5.1)

Барлық параметрлер координа мен уақыттың үзіліссіз функциялары болып табылатындықтан (5.15)-теңдеуді ескеріп келесі теңдеуді аламыз:

(5.1)

Жылу ағынының векторы үшін Фурье гипотенузасын қолданып, мына түрдегі теңдеуді аламыз:

(5.1)

(5.1) және (5.1) теңдеулерді ескеріп, энергияның дифференциалдық теңдеуін аламыз:

Ішкі күштердің жұмысы мен ағынның кинетикалық энергиясы оның энтальпиясымен салыстырғанда аз болған жағдайдағы сұйық ағысының шектелген жылдамдығында бұл теңдеу біршама жеңілдетіледі және мына түрге келеді:

(5.1)

мұндағы: -субстанционалды туынды.

(5.)

Қозғалмайтын орта үшін белгілі Фурье-Кирхгофтың теңдігін аламыз:

(5.)

Жылудың ішкі көздері болмаған жағдайдағы (5.) теңдеуден мынаны аламыз:

(5.2)

мұндағы, -температура өткізгіштік.

(5.2)-теңдеудегі белгісіз шама ретінде сұйықтың қозғалыс жыдамдығы алынады. Осылайша сұйық ағынында температураның таралуын анықтау үшін алдымен гидродинамикалық тапсырманы анықтау керек, яғни сұйық ағынында жылдамдықтың таралуын анықтаймыз.

Сұйық ағынында заттың сақталу заңы: шектелген аудандағы көлемдегі сұйық массасының сақталу заңын мына түрде жазуға болады:

(5.2)

ағын массасының тығыздық векторын енгіземіз,сонда:

(5.2)

көлемде тығыздықтың өзгеруі салдарынан масса жиналады:

(5.2)

(5.2) және (5.2)-теңдеулердегі пен dM-ді (5.23)-теңдеуге қоямыз:

=0 (5.2)

көлем еркін таңдалған, ал сұйықтың барлық параметрлері тұтас орта үшін қабылданған жуықтауларға сәйкес координата мен уақыттың үздіксіз функциялары болып табылады. Сондықтан (5.2)-теңдеуден:

(5.2)

Масса ағынының тығыздық векторы жылдамдық векторы және тығыздықпен қарапайым қатынаста байланысады:

(5.2)

Сонда,

(5.2)

немесе тікбұрышты координатада:

(5.)

Сонымен қатар, тұтас ағыс үшін:

(5.)

Осесимметриялық ағыс үшін:

(5.3)

мұндағы: -нормаль арқылы симметрия осіне дейінгі қашықтық.

Негізгі әдебиеттер: 1 – 4.

Қосымша әдебиеттер: 1-2.

№ 6 дәріс. Конвективті жылуалмасудың ұқсастық теориясы. Жылулық шекаралық қабаттың негізгі теориясы (ЖШҚ)

Жылуөткізгіштік есептерін теориялық әдістермен қарастырғанда біршама математикалық қиындықтар туына байланысты тәжірибелік әдістерді де қолдануға тура келеді. Ал қазіргі замандағы әрбір тәжірибе – күрделі де қымбат зерттеу. Сондықтан тәжірибелік зерттеуді жоспарлағанда, оның нәтижелерін сұрыптағанда кездейсоқ біржақты есепті қарастырмай физикалық проблеманы кеңінен қамтыған дұрыс. Дербес тәжірибенің нәтижелерін неғұрлым саны көп есептер тобына қолдана білу керек. Ол үшін белгілі ерекшеліктеріне қарай ұқсас есептер тобын құрастыру қажет. Мұндай мүмкіншілікті ғылымның әр саласында, әсіресе жылу физикасында жиі қолданылып жүрген ұқсастық теориясы береді.

Ұқсастық теориясында әрбір есеп үшін сол есепке тән және сол есепте қарастыру керек болатын физикалық мағынасы бар өлшемсіз күрделі айнымалылар бар екені дәлелденеді.

Физикалық процесті өлшемсіз шамалар жүйесінде қарастырудың өзіндік артықшылықтары бар:

• айнымалы шамалардың саны азаяды;

• өлшемсіз күрделі шамалар құбылысты сипаттайтын байланыстарды тереңірек анықтайды;

• жаңа айнымалылар өздерінің мағынасы бойынша жалпылама болады.

Сонымен ұқсастық теориясының ең бір маңызды мақсаты – нақты есепті сипаттайтын өлшемсіз жалпылама айнымалыларды қорытып шығару. Ондай айнымалыларды анықтау үшін зерттеліп отырған құбылыстың дифференциалдық теңдеуі мен шарттары жеткілікті.

Біз мысал ретінде геометриялық ұқсас екі денеде жүріп жатқан стационар емес жылуөткізгіштік процестерді қарастырайық. Зерттеу нәтижесінде стационар емес жылуөткізгіштікті қандай өлшемсіз айнымалы сипаттайды, екі есептің қандай ұқсастық белгілері болуы мүмкін, яғни қандай шарттар орындалғанда бір есептің шешімі ұқсас екінші, үшінші, т.б. есептердің шешіміне сәйкес болады деген сұрақтарға жауап берейік. Ол үшін көптеген әдістердің арасынан масштабтық көбейткіштер әдісін таңдап алып екі есептің дифференциалдық теңдеулерін және ІІІ текті беттік шарттарын жазып шығайық.

Бірінші есеп үшін:

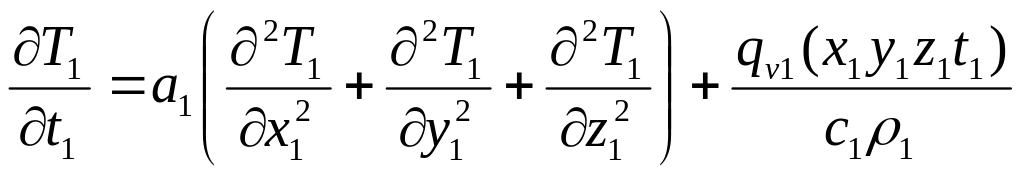(6.1)

(6.2)

Екінші есеп үшін:

(6.3)

(6.4)

Жылуөткізгіштік процесі геометриялық ұқсас денелерде жүріп жатқандықтан, бұл құбылыстарды сипаттайтын өлшемді шамалардың арасында пропорционалдық қатынастар болуы керек екені айқын. Сондықтан біз төмендегідей пропорционалдық коэффициенттерді қарастыра аламыз

Келтірілген коэффициенттерді, яғни масштабтық көбейткіштерді қолдана отырып, бірінші процесті сипаттайтын (6.1, 6.2) теңдеулерді түрлендірейік.

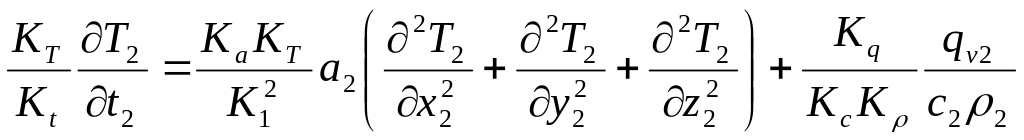(6.5)

(6.6)

Түрлендірудің нәтижесінде бірінші денеде жүріп жатқан жылуөткізгіштік процесін екінші денедегі жылуөткізгіштікке тән өлшемді шамалармен өрнектедік. (6.5, 6.6) теңдеулерге қарағанда, екі есептің шешімдері бірдей болуы үшін, яғни (6.5, 6.6) теңдеулер екінші есепті өрнектейтін (6.3, 6.4) теңдеулерді толық қайталауы үшін теңдеулердің екі жағында пайда болған масштабтық көбейткіштерден құрастырылған комплекстер өзара тең болуы керек. (6.5) теңдеуден

немесе

(6.7)

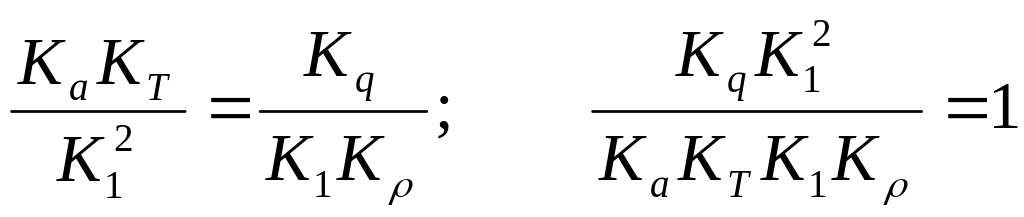
немесе

, (6.8)

мұндағы х₁ және х₂ –нің орындарында дәл солай у немесе z болуы мүмкін.

(6.6) теңдеуден

,

немесе

(6.9)

Сонымен, біз өлшемді шамалардан құрастырылған үш түрлі өлшемсіз комплекстерді қорытып шығардық. Бұлар: ; ; .

Олардың біріншісі Фурье саны температуралық өрістерді уақыт бойынша салыстыруға мүмкіншілік береді. (6.9) формуламен анықталған өлшемсіз комплексті Ві (Био) саны немесе ұқсастық критериі деп атайды. санының құрамына қарасақ, оны тек есептің мазмұны бойынша алдын-ала берілетін өлшемді шамалар құрастырғанын байқаймыз. Сондықтан құрамында тәуелсіз айнымалы уақыт бар Фурье комплексін анықтаушы Фурье ұқсастық саны деп атасақ, алдын-ала есептелетін Био санын ұқсастық критериі деген орынды болады. Келесі өлшемсіз комплексті Остроградский ұқсастық критериі деп атайды.

Жылулық ұқсастық: Практикада пайдалану мақсатында теңдікті түрлендіреді, бұл теңдік ұқсастық критерилерінің функциясы түрінде беріледі. Қабырға мен сұйық арасындағы жылу алмасуды қарастырамыз. Шекаралық қабат арқылы энергия жылуөткізгіштік заңымен таралады. уақыт аралығында өтетін жылу Фурье заңымен анықталады:

(6.10)

Осы жылу шекаралық қабаттан конвективтік әдіспен сұйықтың өзегіне беріледі және жылу беру процесінің негізгі теңдеуімен анықталады:

(6.11)

Орныққан жылуалмасу процесінде қабырғадан сұйыққа берілген жылудың мөлшері өзгермейді; (6.1) мен (6.2) оң жақтағы мүшелерін теңестіреміз:

(6.12)

(6.3) теңдіктің оң жақтағы мүшесін оның сол жақтағы мүшесіне бөлеміз; математикалық операторларды алып тастаймыз. ны ұзындыққа (тік қабырғаның биіктігі немесе құбырдың диаметрі) ауыстырып, өлшемсізшаманы аламыз:

(6.13)

Осындай шаманы Нуссельт критериі деп атайды. Нуссельт критериіқабырға мен сұйық арасындағы жылуалмасу қарқынын сипаттайды. Нуссельт критериіне анықтайтын шама кіреді.

Жылуалмасу процесінің орнықпағанын сипаттайтын мүше қатынаспен шамасына алмастырылуы мүмкін.

Мүшені мүшеге бөліп өлшемсіз шаманы аламыз. Бөлшек сандармен жұмыс істемеу үшін осы шаманы кері шамаға ауыстырып, жылу процесінің орнықпағандығын сипаттайтын, Фурье критериін аламыз:

(6.1)

Конвективтік мүшені шамаға бөліп және қысқартып, конвективтік әдіспен тасымалданылған жылудың жылуөткізгіштік әдіспен тасмалданған жылуға қатынасын сипаттайтын, Пекле критериін аламыз:

(6.1)

Рейнольдс критериі (сұйықтың қозғалу режимін сипаттайды). Өлшемсіз шама сұйықтың жылуфизикалық қасиеттерін сипаттайды, осы шаманы Прандтль критериі деп атайды:

(6.1)

Физикалық процестердің ұқсастық шарттары:

және теңдеулер конвективті жылуалмасу процесін сипаттайды.

Дифференциалдық теңдеулер құбылысты нақты сипаттауға мүмкіндік береді.

Модельдеу шарттары дегеніміз - процесс өтетін ортаның моделі. Модельдеу барысында процестер орындалу үшін келесі ережелерді қолданамыз:

1)Геометриялық шарттар-процестегі дененің пішіні мен өлшемін сипаттайды.

2)Физикалық шарттар-қарастырылып отырған ортаның физикалық қасиеттерін сипаттайды.

3)Шекаралық шарттар-сұйықтың шекарасындағы ағынды сипаттайды.

Динамикалық шекаралық қабат. Жазық дене беті арқылы сұйықтың ағу құбылысын қарастырайық. Ағып келе жатқан ағынның жылдамдығы мен температурасы тұрақты және сәйкесінше ω₀,t₀-ға тең. Сұйықтың молекулалары дене бетімен жанасқанда оған жабысады. Нәтижесінде пластина шекарасында тұтқырлық күші әсерінен тежелген сұйықтан шекаралық қабат пайдаболады. Бұл кезде жылдамдық 0-ден дене бетінің жылдамдығына дейін өзгереді. Осы тежелген сұйықтағы шекарылқ қабатты динамикалық шекаралық қабат деп атайды.

Динамикалық шекаралық қабат теориясын 1904 жылы Прандтль ашақан.

Жылулық шекаралық қабат. Ағын мен пластинаның арасында аналогты түрде жылулық байланыс орнайды. Сұйықтың ыдысқа жабысқан бөліктерінің температуралары болады және ол дене бетінің температурасына тең. Сұйық қабаты сол бөліктермен жанасқанда өзінің жылуын береді де суиды. Сол суыған қабаттар келесі қабаттармен жанасқанда өздерінің жылуын береді. Міне осылай тізбектелген қабаттардың жылу алмасуы салдарынан жылулық шекаралық қабат пайда болады.

Конвективті жылуалмасу процесін модельдеу туралы жалпы түсінік: Конвективті жылуалмасу процесі дифференциалдық теңдеулер жүйесімен сипатталады. Бұл теңдеулерде өлшемдерді 3 түрге бөлуге болады.

1.тәуелсіз- бұл координаттары

2.тәуелді-бұл немесе

3.тұрақты шамалар –бұл т.б.

Өлшеусіз шамалармен қоса теңдеулердің құрамына өлшеусіз комплекстер кіреді. Бұл комплекстер әр түрлі физикалық шамалардан тұрады. Олар :

(6.7)

Осы ұқсастық критерийлері гидродинамикаға үлес қосқан атақты ғалымдардың атымен аталады. Бірінші Нуссельт заңы

(6.8)

Нуссельт саны сұйық шекарасындағы жылуалмасуды сипаттайды.Келесі өлшеусіз комплекс –Рейнольдс саны

(6.9)

Рейнольдс саны сұйықтағы инерция күшімен тұтқырлық күшін сипаттайды.

(6.0)

Өлшеусіз шамаларды да 3-ке бөлеміз:

1.тәуелсіз-бұлар координаттары

2.тәуелді- бұл

3.тұрақты шамалар- бұл

Негізгі әдебиеттер: 1 – 4.

Қосымша әдебиеттер: 1-2.

№7 дәріс. Турбулентті конвективті жылуалмасудың негізі

Сондай-ақ тұтқыр сұйықтың ағысын ламинарлық және турбуленттік деп екіге бөледі. Ламинарлық латынның Lamіna – сызықша, тақтайдай, ал турбуленттік латынның - turbulentus – тынышсыз, ретсіз деген сөздерден алынған.Сұйықтың жеке қабаттары бір-бірімен араласпай, бірінің бетімен екіншісі сырғып параллель қозғалса мұны ламинарлық ағыс деп атайды.

Тұтқыр сұйықтың қабаттарының аралығында пайда болатын ішкі үйкеліс күші сұйықтың қозғалысына әсер етеді. Бұл күштің және түтік қимасының әр жеріндегі сұйықтың жылдамдығының шамасы аз болса ғана сұйықтың ағысы ламинарлы болады. Онда сұйық қабаттарының жылдамдығы түтікше осінен оның қабырғасына қарай параболалық түрде өзгереді. Өсімдіктің, ағаштың сабағының бойымен қоректік шырындардың қозғалуы, судың, мұнайдың топырақ ішінде қозғалуы, потшибниктер бойымен жұқа май қабатының қозғалысы ламинарлық ағысқа мысал болады. Сұйық бөлшектерінің жылдамдығы артып, белгілі шекті мәнге жеткенде әр қабаттардың бір-бірімен араласуын сұйықтың турбулентті ағысы деп атайды. Бұл кезде ағыстың әр нүктесіндегі жылдамдық уақытқа байланысты өзгереді. Сұйық бөлшектерінің бір қабаттан екінші қабатқа өту себебі, олардың ағысқа перпендикуляр бағытталған құраушысы пайда болады. Жылдамдықтар градиенті өте үлкен болғандықтан, түтікшенің сумен жанасар жерінде су құйыны пайда болады.Пуазейль формуласы арқылы сұйықтың, газдың тұтқырлығын анықтауға болады. Ол ламинарлық ағысқа қолданылады да, турбуленттікте пайдаланылмайды.

Турбуленттік ағыста ішкі үйкеліс күшінің артуын жылдамдықтың ағысқа перпендикуляр құраушысының пайда болуымен және тұтқырлық коэффициентінің (h) өсуімен түсіндіруге болады. Табиғатта көбіне сұйықтар мен газдардың турбуленттік ағысы кездеседі. Оған түтікше құбыр бойымен судың ағысы, газда немесе суда қозғалған қатты денемен жанасқан қабаттағы газдың, судың ағысы, жер атмосферасындағы ауаның қозғалысы, т.б. жатады.

Ламинарлық ағысты толықтай тұтқырлық арқылы түсіндірсек, турбуленттік ағыста инерция күшінің ролі зор. Сондықтан ламинарлық ағыстан турбуленттік ағысқа өту инерциялық күштің тұтқырлық күшке қатынасымен анықталады. Бұл қатынасты Рейнольдс саны деп аталатын (Осборн-Рейнольдс (1842-1912) ағылшын физигі) өлшемсіз шамамен сипаттайды.

(7.1)

мұнда - кинематикалық тұтқырлық, r -судың (газдаң) тығыздығы -түтік қимасындағы сұйықтың (газдың) орташа жылдамдығы, D –түтіктің диаметрі.

Тәжірибе нәтижесінде Re –санының шамасы аз болса, (Re<1000) сұйықтың немесе (газдың) ағысы ламинарлық, ал бұл санның мәні үлкен шамамен Re=2300болса, ағыс турбулентті болады.

Рейнольдс саны тұрақты болса, онда әр түрлі сұйықтар мен газдар - қима ауданы түрлі (түтіктермен) құбырларда біркелкі ағады.

Турбулентті және ламинарлы ағыстар арлығындағы сұйық қозғалысының режимі ауыспалы деп аталады.

Сұйық ағысы негізгі ағын және шекаралық қабаттан тұрады. Қатты дене бетінде тұтқыр үйкеліс күшінің әсерінен тоқтатылған сұйықтың жұқа қабаты пайда болады.

Жылуалмасу бетіне қосалқы сұйықтың бөлшектері оған жабысып қалады. Тұтқырлықтың өсуіне және Re санының кемуіне байланысты шекаралық қабаттың қалыңдығының артуы басталады. Неғұрлым Re саны жоғары болған сайын, соғұрлым шекаралық қабат жұқа болады.

Шекаралық қабаттың жұқа болып қалуына қарамастан, ол конвективті жылуалмасу процесінде жоғарғы роль ойнайды. Шекаралық қабаттың екі түрін ажыратады: динамикалық және жылулық. Шекаралық қабат дегеніміз – дене бетіне өте жақын орналасқан жұқа қабаттағы тұтқыр сұйықтың қозғалысы.

Негізгі әдебиеттер: 1 – 4.

Қосымша әдебиеттер: 1-2.

№8 дәріс. Жылуалмасудың гидродинамикалық теориясы

Жылуалмасудың гидродинамикалық теориясы: Жылуалмасудың теңдеуінен шығатындай, температура өрісі және соған қатысты жылу ағынының тығыздығы өрістің жылдамдығына және сұйықтың қозғалысына байланысты. Басқаша айтсақ, температураның өзгеруі сұйықтың физикалық құрамына және қозғалыс тәртібіне де әсер етеді. Гидродинамикада тұтқырлы сұйықты екі басты қозғалыс режимдері анықтайды: ламинарлы және турбулентті. Ламинарлы режимде бөлек қабаттар параллельді және бір-біріне әсер етпей бір бағытта қозғалады. Сұйықтың түрлі қабаттарындағы бөлшектер бір-бірімен араласпайды. Турбулентті режимде газ бөлшектерінің ретсіз қозғалуы салдарынан,оның түрлі қабаттары үнемі араласып отырады. Турбуленттік ағыс-орта бөлшектерінің күрделі, шиеленіскен қозғалысы.

Рейнольдстің критикалық саны ламинарлы режимнен турбулентті режимге өтуді анықтайды. Рейнольдс саны , инерция ағын күшінің тұтқырлық күшіне қатынасын анықтап, осы қозғалыс режимін ашқан О.Рейнольдстің (1842-1912) есімімен аталған. Қозғалыс режимінің ауысуы жүретін Re саны критикалық, деп аталады. өлшемі турбуленттік ағынға, жылдамдыққа, қозғалыс шарттарына және т.б. байланысты.

Егер Рейнольдс саны өзінің кризистік мәнінен төмен болса, онда ағыс ламинарлы болады. Ал егер Рейнольдс саны өзінің кризистік мәнінен жоғары болса, онда ағыс турбулентті болады.

Физикалық және турбуленттік Прандтль саны: Бірге тең ұқсастық тұрақтыларындағы өлшемді шаманың кешендері ұқсастық критерийлері деп аталады. Ұқсастық критерийлері барлық ұқсас құбылыстар үшін бірдей мәндерде сақталады, бірақ олар тұрақты болмайды. Ұқсастық критерийлері нөлдік өлшемді болмайды. Ұқсастықтың негізгі критерийіне Рейнольдс саны жатады:

(8.1)

Рейнольдс саны инерция күші мен тұтқырлық күшінің арақатынасын сипаттайды; егер Рейнольдс санын мына түрде жазсақ көруге болады:

(8.2)

Рейнольдс санының мәні кіші болған сайын, молекулалық тұтқырлық күші барлық гидродинамикалық ағын тәртібіне қатты әсер етіп тұтқырлы, ламинарлы сұйық ағысы тұрақты болып келеді. Кейбір Рейнольдс санының критикалық мәндерінде сұйықтың ламинарлы ағысы турбуленттік ағысқа көшеді. Конвективті жылуалмасудың интевсивтілігі сұйық ағысының режиміне байланысты, сондықтан Рейнольдс саны жылуалмасу теориясында басты анықталатын критерийлердің бірі болып есептеледі. Пекле саны

(8.3)

Пекле саны конвекцияның жылу таралуының интенсивтілігі мен жылуөткізгіштіктің жылу таралу интенсивтілігінің арақатынасын сипаттайды. Пекле санының Рейнольдс санына қатынасы Прандтль санын береді:

(8.4)

Прандтль саны динамикалық және жылулық шекаралық қабат қалыңдығының арақатынасымен байланысты .

Турбуленттік шекаралық қабаттағы жылудың таралуы мен қозғалыс саны теңдеулері былай жазылады:

(8.5)

(8.6)

Бұл теңдеулерді келесі түрде жазып шығайық:

(8.7)

(8.8)

мұнда арқылы қатынасы берілген. шамасын турбуленттік Прандтль саны деп аталады. Турбуленттік қозғалыс саны және жылу таралуының кинематикалық коэффициенттері турбуленттік ағын процессінің параметрлерінен тәуелді. Бұдан шығатыны жалпы жағдайда турбуленттік Прандтль саны процессінің параметрі болып табылады.

Рейнольдс аналогиясы: Егер сұйық пен дене арасында жылуалмасу болса, онда дененің бетінде жылулық шекаралық қабат пайда болады, мұнда температура оның бетіндегі мәнінен қоздырылмаған ағынның мәніне дейін өзгереді. Шекаралық қабат көлденең температура градиентімен сипатталып , сұйық пен қабырға арасындағы жылудың таралуын анықтайды. Жылулық шекаралық қабаттың сыртында жылудың таралуы болмайды.

Қозғалыс саны және жылу таралу процесстерінің аналогиясы .Егер жылу таралу теңдеуінен ішкі жылу көзі бар және жылудың үйкелісі үшін кинетикалық энергияның диссипациясын алып , ал

(8.)

қозғалыс теңдеуінен мүшесін алып тастасақ, онда осы теңдеулерді мына түрге келеді:

(8.1)

(8.1)

Негізгі әдебиеттер: 1 – 4.

Қосымша әдебиеттер: 1-2.

№ 9 дәріс. Пластинаны еріксіз орап ағу кезіндегі жылудың берілуі

Жартылай өткізгіш пластинада, физикалық құрамы тұрақты сығылмайтын сұйықтың үздіксіз ағатын стационар ағынын қарастырайық. Пластинаның температурасын тұрақты және Т_ст тең деп аламыз. Пластина бетінде заттың диффузия құбылысы жүреді деп санайық. Бірақ диффузияның интенсивтілігі айтарлықтай үлкен болмағандықтан, пластинаны өткізгіш емес деп санауға болады. С_ст қабырғасында диффузияланған заттар концентрациясы тұрақты деп саналады. Координатаның бас нүктесіне пластинанның бастапқы нүктесін орналастырамыз, пластинана бойымен х осін орналастырамыз (9.1-сурет). Себебі, пластина өте жұқа және ағыс бойымен орналасқандықтан: .

9.1-сурет. Пластинаны орап аққан кездегі сұйық ағысының бейнесі

Бұл жағдайда шекаралық қабаттың дифферанциалдық теңдеуі (диссипация энергиясы мен термодиффузияны ескермегенде):

(9.1)

(9.2)

(9.3)

(9.4)

Шекаралық шарт:

Егер ; .

Егер .

Егер мәндерін қабылдағанда, теңдіктің сараптамасы жылдамдықтың, температураның және пластинаның ағу кезіндегі шекаралық қабатының концентрациясының арасындағы қатынастарды көрсетуге мүмкіндік береді. Бұл жағдайда теңдеудің динамикалық, жылулық және диффузиондық шекаралық қабатттары біртекті болып, бұл аз жылдамдықта пластина ағыны сығылмайтын сұйықтың және жылумассаалмасу кезіндегі шекаралық қабаттың жылдамдығының, температурасының және концентрациясының таралуына алып келеді:

(9.5)

Көпшілік газдар үшін Pr, Sc, Le сандарының мәні бірлікке жуық болғандықтан, бұл нәтиженің практикада маңызы зор. Тұрақты физикалық қасиетке ие сығылмайтын сұйық ағыны кезінде оның өріс жылдамдығы, өріс температурасы мен өрістың концентрациясына тәуелді емес. Сондықтан, алдымен қозғалыс теңдеуін қарастырып, содан кейін энергия мен диффузия теңдіктерін шешуге қолдануға болады. Берілген есептеулер кезінде шексіз пластинаның ағуы кезіндегі ұзындық мөлшері берілмеген, сондықтан, әр түрлі арақашықтықта аңықталған түрде алынған масштабтағы ағын бойының жылдамдығы қарастырылады. Масштаб ретінде потенциальды ағын жылдамдығын аламыз. Ал, көлденең қимасының ұзындығы ретінде - шекаралық қабаттың қалыңдығы қолданылады. Бұл шарт кезінде жылдамдықты былай жазуға болады:

(9.6)

бұл жерде функциясы барлық арақашықтықтарда бірдей болу керек. Шекаралық қабаттың қалындығы:

(9.7)

Сондықтан тің сапалық масштабы ретінде , бұл жерде

(9.8)

Тоқ күшінің функциясын енгізе отыра бөлінбейтін тендеуді қанағаттандырса:

(9.9)

Блазиусуға сүйенсек тоқ күшінің функциясы мынадай: және өлшемсіз ауыспалы мәндерін енгізе отыра:

(9.10)

Бұл жерде -өлшемсіз тоқ күшінің функциясы.

Мынаны ескере отыра

(9.11)

(9.12)

Қозғалыс теңдеуінен алынған теңдіктерді қысқарта отыра былай жазамыз:

(9.13)

Шекаралық шарты мынадай: .

Теңсіздік үшінші ретті қарапайым сызықты емес дифференциалдық теңдеу болып табылады. Теңсіздіктің шешімі функциясын ретке жіктеу жолымен немесе сандар тәсілімен есептеледі.ь 9.1-кестеде функциясының мәндері және оның туындыларының мәні Хоуартом есептеуі бойынша. Жылдамдықтың қисық өзгерісі және , берілген кесте бойынша есептелген.

Кесте-9.1. функциясының мәндері, оның туындыларының мәні және Хоуартом есептеуі бойынша мәндері көрсетілген

9.2 -суретте есептелген қисық Никурадзенің жүргізген тәжірибелік есептеулерімен салыстырылады.

Есептеулердің шешімі барлық қажет шекаралық қабаттың динамикалық сипаттамаларын шешуге мүмкіндік береді.

(9.14)

Cәйкесінше өлшемсіз қабырғаның үйкеліс қуаты

(9.15)

Ал үйкеліс коэффициенті

(9.16)

9.2 –сурет. Есептелген сан мәндердің тәжірибемен салыстыру негіздері

Шекаралық қабаттың қалған барлық сиппаттамаларын аналогиялық түрде есептеуге болады. Шекаралық қабаттың қалыңдығын қабырғаның ара-қашықтығымен, яғни , 9.1-кестеден . Ал шекаралық қабат қалыңдығы:

(9.17)

Шығару қалыңдығын мына теңдеуден алуға болады:

(9.18)

мұндағы мәні шекаралық қабаттан тыс жатқан нүктенің кез келген мәніне сәйкес. 9.1-кестедегі .

9.3-сурет. Ағыс жылдамдығының коэффициенті

Сондықтан

(9.19)

Импульсті жоғалту қалыңдығын аналогиялық түрде анықтаймыз:

(9.20)

Бұл теңсіздіктерден импульсті жоғалту қалыңдығынан құралған Рейнольдс санының үйкелісінің тәуелділік коэффициенті:

(9.21)

Енді тоқ теңдеуін шешуге кірісеміз. мәндері қатынасын анықтайық, энергияның теңдеуін температураның әр түрлілігінің қатынасы:

(9.22)

Қарапайым дифференциалдық теңдеуді аламыз

(9.23)

Шекаралық шарттар егер ; егер .

Бұл теңдеу айнымалыларды бөлу жолымен интегралдап қорытындылаймыз.

Қабырғадағы температура градиенті:

(9.4)

Температура градиентінің ұзындығын дифференциалдық теңдеу арқылы табамыз:

(9.5)

Негізгі әдебиеттер: 1 – 4.

Қосымша әдебиеттер: 1-2.

№ 10 дәріс. Еркін конвекция шартындағы (ЕКШ) және құбырдағы сұйықтың еріксіз ағысы кезіндегі жылудың берілуі. Құбырдың сыртын орап аққан кездегі жылудың берілуі

Сұйық еркін қозғалған кездегі жылуалмасу: Грасгоф критериін формуласымен есептейміз, ал Прандтль критериін анықтау үшін формуласын қолданамыз.

Егер және болса, онда тік қабырғаның бойында сұйықтың еркін ламинар қозғалысы орнығады.

Орташа жылу беру коэффициентін анықтау үшін мынандай теңдеулерді қолданамыз:

а) егер болса, онда

(10.1)

б) егер болса, онда

(10.2)

(10.1) және (10.2) теңдеулерде анықтайтын температура ретінде ыстық қабырғадан алыс орналасқан сұйықтың өзегіндегі температура, ал анықтайтын өлшем ретінде құбырдың (қабырғаның) биіктігі қабылданған.

Егер болса, онда тік қабырғаның бойында сұйықтың еркін турбулентті қозғалысы орнығады. Орташа жылу беру коэффициентін анықтау үшін келесі формуланы қолданамыз:

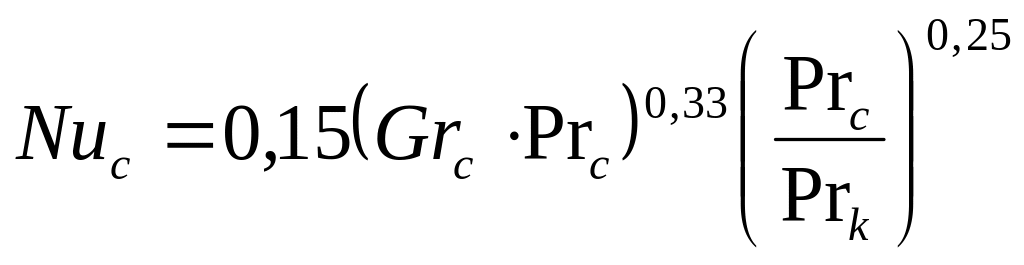(10.3)

Құбырдан қоршаған ортаға (сұйық) берілген жылудың мөлшері келесі формула негізінде есептелінеді:

(10.4)

Сұйық құбырмен еріксіз қозғалған кездегі жылуалмасу: Рейнольдс критериі: , мұндағы сұйықтың жылдамдығы, м/с; құбырдың ішкі диаметрі, м; сұйықтың тұтқырлығы, м²/с.

Температура тегеуіріні:

(10.5)

Грасгоф критериі:

(10.6)

мұндағы орта (сұйық, газ немесе бу) көлемінің температуралық ұлғаю коэффициенті, 1/К; м²/с – еркін түсу үдеуі.

Құбыр ішінде ламинар қозғалыс орныққан болса Нуссельт критериін анықтау үшін келесі формула қолданылады:

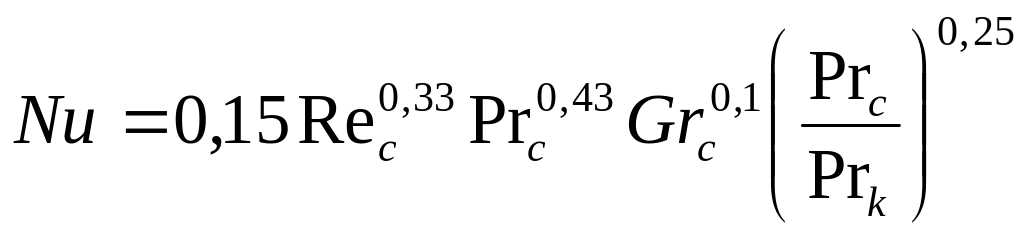(10.7)

Егер құбырдың ішінде турбулентті қозғалыс орныққан болса :

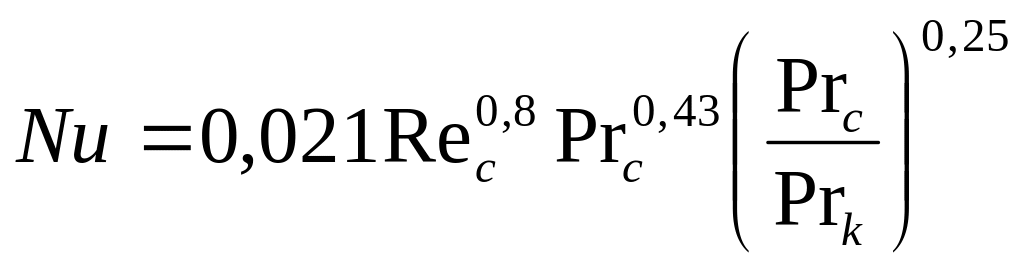(10.8)

Индекстер: сұйықтың орташа температурасында анықталатын критери; қабырғаның температурасында анықталатын критерий.

Нуссельт критериі: . Егер : болса, онда есептеп табылған жылу беру коэффициентіне түзету енгізіледі.

Нақты жылуалмасу коэффициенті:

(10.9)

Сұйықтан қабырғаға берілген жылудың мөлшерін келесі формуламен анықтаймыз:

(10.10)

Сырттан орап ағу кезіндеги жылу берілу: Инженерлік практикада көлденең құбырды орап ағып өтетін жылуалмасу құбырларының жылу берілу коэффициентін жиі есептейді. Құбырдың гидродинамикалық орналасуы күрделі құбылыс. Шахматты шоғырларға түзету енгізілмейді.

Газ жылдамдығы құбырдан қисық ағу кезінде шартты түрде газ жүрісіндегі жазық қимаға жатады. Шахматты шоғырларды құбыр қандай жерде орналасса да, оның жоғары жылу берілуі маңдайлық нүктесінде сақталады. Бұл шоғырлардағы бірінші реттегі құбырлардың сипаттамасы келесі реттегі құбырлардан ерекшеленбейді.Каналға орналастырылған цилиндр. Құбырларды ағызу кезіндегі ағын жылдамдығы көлденең қимасының интегралының орташа жылдамдығымен сипатталады.

Осындай орап ағу құбырларын ұйымдастыру үшін, кейбір жылуалмастырғыштарда сегментті қиылған қоршаулар қарастырылған. Бұл жағдай құбырдағы орап ағу сипаты дәлізді шоғырларда күрделі болатынына байланысты. Себебі дәлізді шоғырларда калориметр периметрі бойынша температураның таралуы біртексіз. Жылуалмастырғыштардағы жылу берілу реттелу үшін құбырдың диаметрін азайтамыз. Диаметрдің өзгеруі құбырды сыртынан орап ағу кезіндегі жылу берілуге әсер етеді. Диаметрдің кішірейюі өз кезегінде шоғырлардың өлшемдерінің кішіреюіне және құбыр санының көбеюіне әкеледі. Бұл жылуалмастырғыш аппараттарды жасауды күрделендіреді. Көлденең орап ағу құбырларындағы жылу берілу процестерінде ерекшеліктері бар. Олар құбыр бетімен ағып өтетін қозғалысты гидродинамикалық тұрғыдан түсіндіреді. Егер Рейнольде саны көп болса, орап ағып өтетін құбырларда құйынды пада болады. Цилиндрдің алдыңғы және артқы жартыларындағы шайылу шарттары және сипаттамалары мүлдем әр түрлі.

Негізгі әдебиеттер: 1 – 4.

Қосымша әдебиеттер: 1-2.

№ 11 дәріс. Таза бу конденсациясы (ТБК) кезіндегі жылуалмасу

Таза бу конденсациясы кезіндегі жылумассаалмасу процестерінің ерекшеліктері: Конденсация дегеніміз будың немесе газдың, сұйық немесе қатты түрге ауысуын айтамыз. Бу турбинасының конденсаторда бу суытқыш құбырда конденсацияға түседі. Сонымен қатар, будың конденсациясы көптеген жылумассаалмасу аппараттарында және сығылу қондырғыларында жүзеге асырылады. Фазалық ауысу кезінде жылудың бөлінуі бу конденсация процесімен үздіксіз байланыста болады. Жалпы конденсация процесі днегеніміз - газдың және будың критикалық жағдайға дейінгі кезінде ғана байқалады және ол суыту жолымен жүргізіледі. Конденсация қандай жағдайда бу көлемінде жүргізілсе тура сондай жағдайда жылуалмасудың суыту бетінде жүреді. Конденсацияның бірінші жағдайында буға енгізілетін суық сұйық және қатты бөлшектерде және қаныққан температураға қатысты будың суыту мәнінде конденсациялық фаза өздігінен түзіледі. Конденсациялық фазаның пайда болуы энергетикада және көптеген техникалар мне өндірістік салаларда жылуалмасудың суытылатын беттерінде будың сұйыққа айналуы жиі кездеседі. Бұл жерде конденсацияға түсетін будың құрамы ешқандай бу және газ қосылысынан тұрмайды, таза буды қарастырсақ. Егер қарастыратын беттің температурасы берілген қысымда қаныққан температурадан кіші болатын болса , онда жылуалмасудың қатты беттерінде қаныққан және қыздырылған будың конденсациясы болады. Беттерде қалыңдығы молекула аралық күштің эффективті әсерлесуінің ара қашықтығынан асатын конденсат қабығы пайда болады. Бұл жағдайда дене беті конденсациясының жеке тамшысымен жабылуы мүмкін. Конденсацияның бірінші түрі сұйық конденсацияның фаза жылуалмастырғыш бетінде орыныққан ( фаза ) қабықша түрінде түзіледі және қабықшалы конденсация деп аталады. Егер конденсат жылумассаалмасу бетін шайып өтетін болса онда бұл жерде қабықшалы конденсация пайда болады. Ал егер шайып өтпеген болса онда тамшылы конденсация деп аталады. Жалпы жағдайда шайып өту құбылысы негізінде қатты денеде пайда болады.

Қатты қабырғалы бетті аламыз. Егер қабырға мен газдың тартылыс күштері қатты денемен сұйық арасынан үлкен болса, мұнда , бұндай жағдайда сұйық қатты дене бетін шайып өтеді. Тамшылы конденсация шофобизатор деп аталады бұл заттың көбігімен жасалады. Бұл зат жылумассаалмасу беттерінде жоғалуы мүмкін. Су буының тамшылы конденсациясы кезінде жылу беріліу қабықшалылығына қарағанда бірнеше есе үлкен. Бұл дегеніміз конденсация бетінен қабықшаға ауысуда жылуды беру кезінде термодинамикалық кедергінің пайда болуы әсерінен ерекшеленеді. Тамшылы конденсацияда қабықшаны бөлу күшінде бұл кедергі бірнеше есеге кіші болады. Егер бұл процесті қарастыратын болсақ, термодинамикалық кедергілер әсері ерекшеленеді бұл процесті келесі суретте көрсетеміз.

(11.1)

Мұнда екі қосылғыш ескеріледі. 2 – ші қосылғыш фаза аусыу кезіндегі пайда болатын шекарадағы термодинамикалық кедергі. Бұл пайда болуы бу және судың фаза көлемінің шекарасындағы температура өзгерісімен негізделеді.

(11.2)

Бұл жердегі фаза шекарасы арасынан өтетін жылу фазалық ауысудағы жылу бет температурасы және ол келесі өрнекпен өрнектеледі.

(11.3)

мұндағы, j – бірілік бетке қатысты ағынның мөлшері, .

Бірінші текті фазалық ауысу: Фаза деп күрделі жүйенің басқа бөліктерінен өзгеше және олардың айқын шекара арқылы бөлінген физикалық біртекті аймақты айтады. Екі фазалық жүйенің мысалы сұйық және қаныққын бу, сұйық және кристалл, бір заттың екі кристаллдық модификациясы тағы басқалар. Фазалары тепе-теңдікте болатын жүйенің сыртқы әсері өзгергенде (айталық жүйеге жылу берілсе немесе жүйе сыртөы ортаға жылу бөліп шығарса) фаза ауысу процесі қайтадан жүреді де зат мөлшері бір фазадан екінші ауысады (қайнау, балқу). Сондықтан фазалық тепе-теңдіктің талаптарын қарастыра отырып, фазалық ауысудың барысын да зерттейміз. Қысым мен температура тұрақты болғанда фазалық ауысуды қарастырайық. Екі фазалық жүйенің термодинамикалық потенциалы қысым p мен температура T және әр фазадағы моль сандарынан N₁, N₂ тәуелді.

Ф=Ф(T, p, N₁, N₂) (11.4)

(11.5)

мұндағы – бірінші және екінші текті фазалардың химиялық потенциалдары. (11.5)-теңдеуді басқаша былай жазуға болады:

(11.6)

Жүйенің қысымы мен температурасы тұрақты болсын. Бұл параметрлердің градиенттері нольге тең болғандықтан қарастырылып отырған жүйе осы параметрлер бойынша тепе-теңдікте болады. Жүйедегі фазалардың моль сандары N₁, N₂ әртүрлі болсын. Теңесу процесі кезінде осы параметрлер қалай өзгеретінін қарастырайық. Егер жүйеде теңесу процесі жүретін болса, онда жоғарыда қарастырғанымыздай термодинамикалық потенциал өзгерісі кемиді dФ<0 . Жүйенің моль сандары тұрақты болса, dN₁,=-d N₂. Сонда

(11.7)

бұдан болуы үшін шарты орындалуы керек, керісінше болса, болады. Сонымен фазалық ауысу кезінде зат молшерінің ағыны химиялық потенциалы көп фазадан химиялық потенциалы аз фазаға қарай бағытталады.

Термодинамикалық тепе-теңдік күйде жүйенің термодинамикалық потенциалы минимум dФ<0, бұдан екі фазаның химиялық потенциалдары теңгеріледі: μ₁(T, p) = μ₂(T, p). Жылу ағыны процесінде температураның, диффузия процесі кезінде қоспаның концентрациясының мағынасы қалай болса, фаза ауысуында фазаладың химиялық потенциалдарының мағынасы сондай. Энергия, масса ағындары температура, концентрасия градиенттеріне байланысты болса, фазалық ауысу химиялық потенциал градиентіне байланысты. Фазалық ауысу процесінде зат мөлшерінің ағыны химиялық потенциалдың градиентінің кемуіне бағытталады да, нөлге айналғанда μ₁(T, p) = μ₂(T, p) тоқталады. Егер күрделі жүйенің температурасы мен қысымы тұрақты, ал бірінші фазаның химиялық потенциалы екінші фазаның химиялық потенциалынан көп болса, яғни μ₁(T, p) > μ₂(T, p), онда молекулалардың бірінші фазадан екінші фазаға өту процесі қайтымсыз адиабаттық процесс болады және бұл процесте энтропия жоғарылайды. Екі фазалы жүйені химиялық потенциалдары μ₁(T, p) > μ₂(T, p) болсын, онда фазалардың ішкі энергиясының өзгерісі:

(11.8)

Фаза ауысуы кезінде жүйенің энтропия өзгерісі:

жоғарыдағы теңдеулерден әр фазаның энтропия өзгерістерін dS₁ мен dS₂ анықтап төмендегі теңдеуге қойсақ:

(11.9)

Бұл процесс тұрақты көлемде және ішкі энергия өзгерісі тұрақты жағдайда өтеді. Бірақта зат мөлшері бірінші фазадан екінші фазаға ауысады. Сонда (42)-теңдеуден екені шығады. Жоғарыдағы шарт бойынша , Т>0. Сонымен әртүрлі фазадан тұратын жүйеде тепе-теңдік күй қалыптасу үшін фазалардың температурасы мен қысымы және химиялық потенциалдары теңгерілуі керек, яғни

T₁=T₂=T; p₁=p₂=p; μ₁(T, p)=μ₂(T, p) (11.10)

жоғарыдағы теңдеу химиялық потециалдың бір аргументін екінші аргумент арқылы анықтауға мүмкіндік береді. Бұл теңдеу фазалық айналу процесінде фазалардың химиялық потенциалы үздіксіз өзгеретінін көрсетеді. Жалпы алғанда фазалардың химиялық потенциалының туындылары фазаның молярлық көлемі мен молярлық энтропиясын береді. Бірінші текті фаза ауысуы кезінде фазалардың химиялық потенциалдары үздіксіз өзгереді де, ал температура мен қысым бойынша алынған дифференциалдары фазалардың фазаның молярлық көлемдері мен молярлық энтропиялары секірмелі өзгереді. Фазалық аысу тұрақты температудада болса, қайтымды процесс үшін теңдеуінен энтропияның секірісі және молярлық жылу мөлшері (жүйеге сырттан берілген немесе фаза ауысу кезінде жүйеден бөлініп шыққан жылу мөлшері) мына формула арқылы табылады:

(11.11)

Бірінші текті фазалық ауысуда , . Сонымен бірінші текті фазалық ауысу деп жүйенің сыртқа жылу беріп немесе сырттан жылу алып жүретін процесін айтады. Бірінші текті фаза ауысуына заттың агрегат күйінің өзгерістері және мқатты дененің бір кристалдық модификациядан басқа кристалдық модификацияға өтуі жатады. Молярлық ауысуды энергия принципіне сәйкес былай жазуға болады:

(11.12)

мұндағы А - заттың бір молінің бірінші фазадан екінші фазаға ауысуы кезінде жасалатын жұмыс. I - фазалардың молярлық энтальпиясы. Сондықтан λ шамасын көбінесе фазалық ауысу энтальпиясы деп атайды. Енді жазықтығында тепе-теңдік қисығының дифференциалдық теңдеуін қорытып шығарайық. Бірінші текті фазалық ауысу қиығы бойында заттардың химиялық потенциалдарының үздіксіз өзгерісінен . Химиялық потенциалдың толық дифференциалдық теңдеуінен фазалық ауысу қисығының дифференциалдық теңдеуін аламыз:

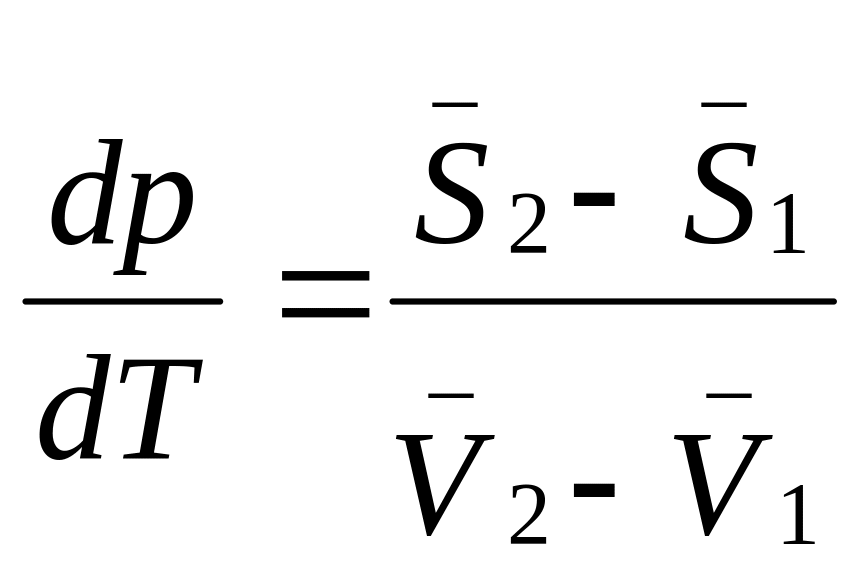(11.13)

Бұл теңдеуді жоғарыдағы теңдеумен салыстырсақ, мына түрге келеді:

(11.14)

бұл теңдеу Клапейрн-Клаузиус теңдеуі деп аталады. Бұл теңдеуден фазалық ауысу жылуы λ>0 болғанда және болса. dp/dT>0 болады. Клапейрн-Клаузиус теңдеуі бірінші текті фазалық ауысуға арналған есептерді шығаруға қолданылады. Бір А шамасының фазалық тепе-теңдік қисығының бойында қысымнан және температурадан тәуелділігін қарастырайық. Ол үшін мына теңдеулерді қолданамыз:

Бұл теңдеулер фазалық тепе-теңдік қисығының бойындағы туындыларды көрсетеді.

Бірінші текті фазалық ауысу процесінде диаграмма қысым мен температураның үздіксіз өзгерісін көрсетеді. Фазалық ауысу процесін T-V диаграммасында қарастырсақ. 11.1-суретте көрсетілгендей берілген қысымда фазалық ауысу температурасында фазалардың молярлық көлемдері секірмелі өзгереді, яғни .Бірінші текті фазалық ауысу процесін сапалық түрде қарастыру үшін S-V диаграммасын қолданамыз.

Әрбір екі фаза үшін термиялық және калориялық күй теңдеулері мына түрде жазылады:

(11.15)

11.1-сурет. Фазалық ауысу температурасында фазалардың молярлық көлемдерінің секірмелері көрсетілген

11.2-суретте көрсетілгендей бірінші текті фазалық ауысуда бірінші фазаның изобаралары мен изотермалары I қисығында бітеді де, фазалардың молярлық көлемдері мен молярлық энтропиялары секірмелі түрде өзгереді (пункт сызық).

11.2-сурет. бірінші текті фазалық ауысуда бірінші фазаның изобаралары мен изотермалары көрсетілген

II қисықта екінші фазаның изобарлары мен изотермалары басталады. I және II қисықтардың арасы энтропия мен көлем үшін тиым салынған аймақ деп аталады. Бірінші текті фазалық ауысуды p-V диаграммасында қарастырайық. Ван-дер-Ваальс теңдеуі: заттың сұйық және газ күйін жобалап сипаттайды. Бұл теңдеудің изотермасы 11.3-суретте көрсетілген. Irq2 қисығы заттың сұйық фазадан газ күйіне ауысуын сипаттайды.

11.3-сурет. Заттың сұйық фазадан газ күйіне ауысуын сипаттайтын диаграммасы

Изотермалық процесте жұмыс еркін энергияның өзгерісімен анықталады. 1rq2 изотермасындағы жұмыс:

. (11.16)

Сұйық пен газдың химиялық потенциалдары теңдеуінен , мұнан

(11.17)

яғни, изотермалық процесте жұмыс Ван-дер-Ваальс қисығы бойынша интеграл 1-2 изобарамен шектелген төртбұрыш ауданына тең. Бұдан I және II аудандар өзара тең екенін көреміз.

Фаза ауысу процесінде тұрақты температура мен қысымда фазалардың химиялық потенциалдарының қиылысуын сапалық түрде қарастырайық

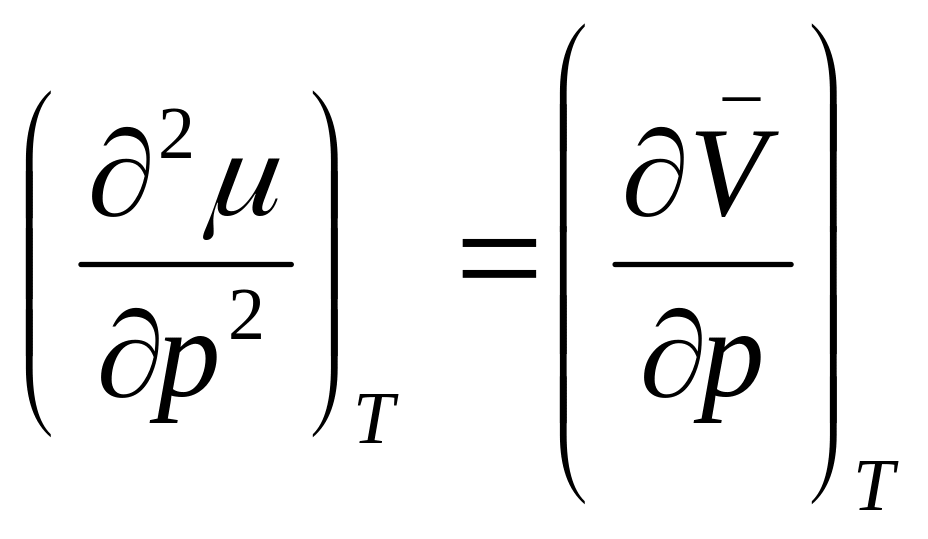, (11.18)

осы теңдеуге сәйкес фазалардың химиялық потенциалдары температура тұрақты болғанда, қысымға байланысты өзгерісі 11.4-суретте көрсетілген. Қиылысу нүктесінің абциссасы берілген температурадағы фазалық ауысу нүктесінің қысымын анықтайды.

11.4-сурет. Фазалардың химиялық потенциалдары температура тұрақты болғандағы қысымға байланысты өзгерісі көрсетілген.

Суреттегі стрелкалар қысымның өзгерісіне байланысты фазалық ауысуды сипатайды. Сонымен қысымның ұлғаюына жүйе үлкен молярлық көлемдегі фазаның кіші молярлық көлемдегі фазаға ауысуы арқылы жауап береді

Екінші текті фазалық айналу: Екінші текті фазалық ауысу жылу алмасуынсыз жүреді және фазалардың химиялық потенциалдарының бірінші ретті туындыларында молярлық көлем мен молярлық энтропия өздңксңз өзгереді. Екінші текті фазалық ауысуға магнетиктің ферромагнетиктен парамагнетикке ауысуы жатады. Екінші ретті фазалық ауысу нүктесінде симметрияның секірмелі өзгерісі атомдардың өте аз санының орын ауыстыруына немесеолардың өте аз қашықтыққа орын ауыстыруына байланысты.

Негізгі әдебиеттер: 1 – 4.

Қосымша әдебиеттер: 1-2.

№ 12 дәріс. Сұйық қайнаған (СҚ) кездегі жылудың берілуі

Қайнап тұрған сұйықты қарастырамыз. 12.1-суретте қыздыру бетінде (шәйнектің түбі, экрандық құбырдың ішкі беті) пайда болатын көпіршіктер көрсетілген.

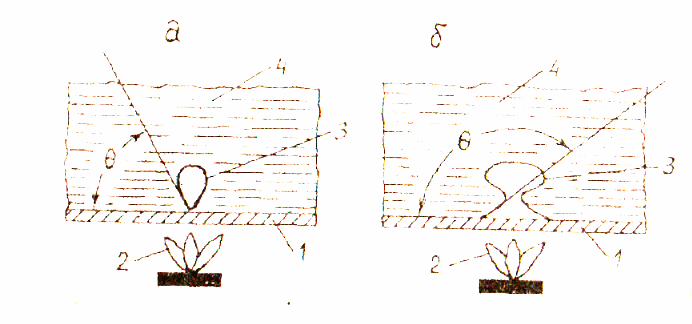
1-қыздыру беті; 2-алау; 3-көпіршік; 4-қайнап тұрған сұйық; жиектік жұғу бұрышы.

12.1-сурет. Қыздыру бетінде пайда болатын көпіршіктердің көрінісі: а) сұйық жұғатын бет; б) сұйық жұқпайтын бет.

Сұйық жұғатын беттерде жиектік жұғу бұрышы үшкір, ал сұйық жұқпайтын беттерде жиектік жұғу бұрышы доға болып келетін көпіршіктер пайда болады. Қайнау процесі өтіп жатқан кезде көпіршік қыздыру бетінен үзіліп шығады, сөйтіп ол шардың пішінін қабылдайды (12.2-сурет). Жылу қабырғадан өтіп сұйыққа беріледі, осыдан кейін ол көпіршікке беріледі. Көпіршіктің ішінде бу түзілу процесі өтеді. Сол кезде көпіршіктің көлемі өседі. Көпіршіктің тығыздыңы сұйықтың тығыздығынан едәуір төмен, сондықтан ол төменнен жоғары қарай қозғалады.Сұйықтың бетіне жеткен кезде көпіршік жарылады, бу сұйықтың үстіндегі кеңістікке түседі.

1-қыздыру беті; 2-алау; 3-көпіршік; 4-қайнап тұрған сұйық; 5-бу кеңістігі; жылулық жүктеме; жылу беру коэффициенті

12.2-сурет. Көпіршіктің судан бөлініп шығу бейнесі

1- көпіршікті қайнау режимі; 2- қыздыру бетінде будың жұқа қабаты пайда болған кездегі қайнау режимі; қайнау дағдарысы орнаған кездегі температура айырымы

12.3-сурет. Қайнау режимдері көрсетілген

12.3-суретте қайнау режимдері көрсетілген. жылулық жүктеме; жылу беру коэффициенті; қыздыру бетінің температурасы мен қайнап тұрған сұйық температурасының айырымы.

2.3-суретте қайнау дағдарысына сәйкес келетін экстремум бар. қайнау процесін екі режимге бөліп тұр. 1- көпіршікті қайнау режимі ( өскен сайын мен елеулі өседі); 2- қыздыру бетінде будың жұқа қабаты пайда болған кездегі (12.4-сурет) қайнау режимі ( өскен сайын мен күрт құлайды).

1-қыздыру беті; 2-алау; 3-көпіршік; 4-қайнап тұрған сұйық; 5-бу кеңістігі; жылулық жүктеме; жылу беру коэффициенті

12.-сурет. Көпіршіктің судан бөлініп шығу бейнесі

Қыздыру бетінде пайда болған будың жұқа қабаты елеулі термикалық кедергі болып табылады, берілген жылуды сұйық толық қабылдамады, осының нәтижесінде шәйнектің түбі немесе қазандықтың экрандық құбыры күйіп кетеді. Ал бұл ірі апатқа алып келуі мүмкін. Сондықтан сұйықты екінші режимде қайнатуға ұмтылмай керек.

Негізгі әдебиеттер: 1 – 14.

Қосымша әдебиеттер: 15-32.

№ 13 дәріс. Мөлдір ортадағы жылулық сәулелену теориясының негізі

Сәулелік жылуалмасу: Жылуберілу процесін екі категорияға бөліп қарастыруға болады. Біріншісі жылуалысу жолындағы ортаның структуралы элементтері жылуалмасу процестеріне қатыса алады. Бұл қарастырылып отырған жылуберілу немесе конвекция. Екінші категория бұл жағдайда орта жылуалмасуға қатыса алмайды. Яғни жылулық сәулелену деп аталады. Жылулық сәулелену тек қана шағылатын дененің оптикалық қасиеті мен температураға негізделген электромагнит толқын көмегімен жылудың таралу процесі. Бұл кезде дененің немесе ортаның ішкі энергиясы сәулелену энергиясына ауысады.заттың ішкі энергиясының сәулелену энергиясына айналу процесінде сәуленің тасымалдануы және оны заттың жұту құбылыстарын сәулелік жылуалмасу процестері деп атаймыз.

Электромагниттік тербелісті толқын ұзындығы мен жиілік арасындағы байланыс арқылы алуға болады.

(13.1)

-вакуумдағы жарық жылдамдығы

Жылулық сәулелендірумен, сәйкес келетін толқын ұзындығының үлкен бөлігі жарық сәуленің толқын ұзындығымен сәйкес келмейді. Толқын ұзындығының термиялық диапозонымен анықталған сәулелендіру инфрақызыл деп аталады, инфрақызыл сәулелену өзіне белгілі толқын ұзындығынан тұрады. Бұл интегралды сәулелену деп аталады. Бірақ жылулық сәулелену толқын ұзындығының барлық диапазонындағы тек қана бір немесе бірнеше бөліктерде пайда болуы мумкін.яғни бұл сәулелену спектральды сәулелену деп аталады. Жылулық немесе жарық сәулеленудің табиғаты,физикалық құрамы да бірдей болып табылады. Сондықтан табиғаттағы таралу,шағылу,сыну заңдары көрінетін сәулелерге ғана емес сонымен қатар жылулық сәулелену үшін де қарастырылады.

Жылулық сәулелену заңдары: Реал қатты денелердің сәулелену спектрлерінің әр түрлілігі соншалық оларды аналитикалық байланыс арқылы сипаттау мүмкін емес. Дәл солуақытта абсолют қара дене өзіне түскен сәулені толығымен жұтады,мұндай дененің сәулелену энергиясының таралу спектрі универсалды. Осыған байланысты жылулық сәулеленудің есептік негізі абсолют қара дененің сәулелену заңы болып табылады.

Планк заңы: Денемен шағылысатын энергия оның температурасымен анықталады. Дегенмен толқын бойымен энергияның таралуы біртекті жүрмейді. Бұдан басқа, энергияның сәулеленуі дискреттік,ол белгілі бір мөлшерлермен квантармен жүзеге асырылады. 1900жылы М.Планк әр түрлі температурада толқын бойымен интенсивтіліктің таралу заңын жазды

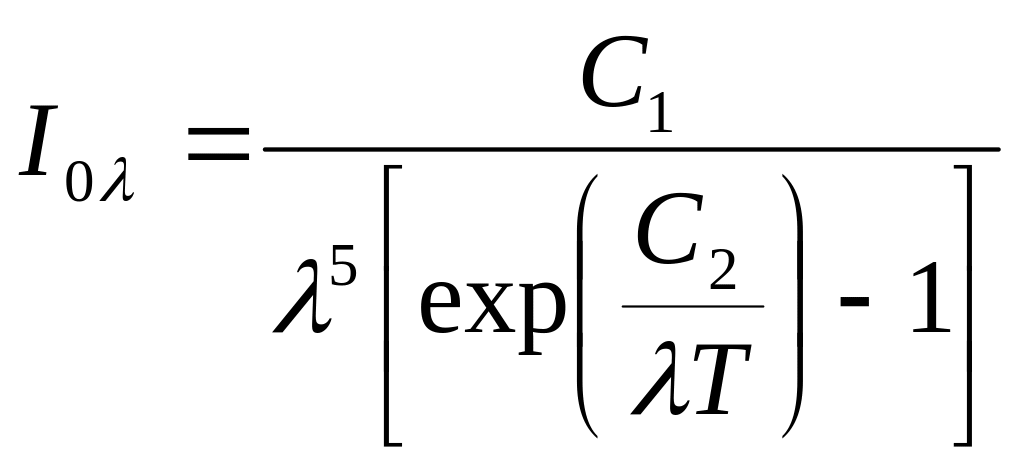(13.2)

Абсцисса осімен, изотерма және ординатамен шектелген аудан толқын ұзындығының интервалында уақыт бірлігінде температура кезінде энергия мөлшерінің өлшемінің қызметін атқарады.

(13.3)

нүктесіндегі сәулелену энергиясы толқын ұзындығының белгілі бір анықталған интервалында ғана шекті мәнге ие болады, себебі шекті мәндегі сәулелену энергиясының қосындысы барлық спектр бойымен таралады. Ендеше жалғыз толқын ұзындығы үшін қатаң монохроматты сәулелену теориялық жағынан мүмкін емес болып табылады,себебі ол шектік энергияға ие бола алмайды. Планк заңының математикалық түріне талдағанда (14.3)-теңдеу 2 жағдайға назар аудару қажет:

және . болған жағдайда қатынас мына түрде болады. . Енді егер шамасын көрсеткіш бойынша қатарларға бөлсек:

(13.4)

Онда шамасының аздығына байланысты қатардың алғашқы 2 мүшесімен шектелуге болады. Бұл жағдайда (13.3)-теңдеу Релей-Джинс формуласына ауысады:

(13.5)

болғанда, онда Планктың нақты формуласымен есептеулердің нәтижелері пайыздан артық емес шамаға сәйкес болады. болған екінші жағдайда шамасы үлкен болады және (13.1)-теңдеуден Вин формуласын аламыз:

(13.6)

Егер болса, онда нәтиже Планк заңымен есеплелген нәтижеден пайыздан да аз шамаға ерекшеленеді.

Вин ығысуларының заңы: Белгілі бір толқын ұзындығындағы әрбір изотерма үшін сәулелену интенсивтілігінің максимал мәніне сәйкес келеді. Сондай-ақ жоғары температуралар үшін экстрималды мән қысқа толқындарға қарай ығысады. Сәулелену интенсивтілігінің ең үлкен мәнін анықтау үшін туындысын нөлге теңестіру қажет:

(13.7)

Бұл жазылған теңдеуде толқын ұзындығы сәулелену интенсивтілігінің максималды мәніне тең, яғни . Теңдеудің шешімін мына түрде жазуға болады:

(13.8)

немесе, мәнін қойсақ:

мм*К (13.9)

Бұл теңдеу- Вин ығысу заңдарының математикалық түрі болып табылады. Заң температура сәулелендіргіші мен сәулеленудің ең үлкен интенсивтілігіне сәйкес келетін толқын ұзындығы арасында байланыс орнатады. Енді шамасын біле отырып, Планк заңы бойынша сәулелену интенсивтілігінің максималды мәнін анықтауға болады:

(13.10)

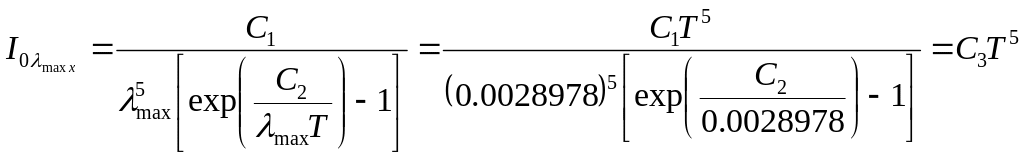
Яғни, ең үлкен сәулелену интенсивтілігі қара сәулелендіргіштің абсолют температурасының 5 дәрежесіне тең.

Стефан—Больцман заңы: Планк заңы сәулелену интенсивтілігінің толқын ұзындығына тәуелділігін анықтайды. Уақыт бірлігінде бірлік ауданда абсолют қара дененің энергия мөлшерінің қосындысы Стефан- Больцман заңы бойынша анықталады. Бұл заңды Стефан эксперименталды түрде- 1879 жылы, ал Больцман теориялық түрде 1884 жылы анықтады, Т температурасы кезінде абсолют қара дене шығаратын толық энергия мөлшерін (14.3)-теңдеуді интегралдап алуымызға болады:

(13.11)

Жаңа шамасын енгізейік , онда , бұдан , бірақ , ендеше,

(13.12)

Алынған нәтижелерді бастапқы теңдеуге қоямыз:

(13.13)

(13.14)

Интегралды бөліктеп аламыз. Интеграл астындағы функцияны қатарға жіктей отырып

(13.15)

Осыдан алатынымыз

(13.16)

(13.17)

мұндағы Вт/(м *К )

Бұл шаманы Стефан- Больцман тұрақтысы деп атаймыз. Абсолют қара дене щығаратын толық энергия мөлшері сәулелендіргіштің температурасының төртінші дәрежесіне тура пропорционал. Техникалық есептеулерде Стефан- Больцман заңын мына түрде қолдану ыңғайлы:

(13.18)

мұндағы - абсолют қара дененің сәулелендіру энергиясы. Стефан- Больцман заңы сұр денелер үшін де қолданылуы мүмкін. Ол үшін қаралық дәрежесі деген ұғым енгізіледі, ол тура сондай температурада сұр дененің сәулелік ағыны шамасын абсолют қара дененің ағын шамасына қатынасымен анықталады:

(13.19)

(13.20)

мұндағы -қаралық дәрежесі, сұр дененің сәулелендіру коэфффициенті, .

Стеффан- Больцман заңының аналитикалық түрі:

(13.21)

мұндағы , -интегралдау тұрақтысы, біртекті сәулеленудің меншікті энергиясы.

Кирхгоф заңы: Дененің сәулеленетін және жұтатын қасиеттерінің арасында байланыс орнатады. Бірінің сәулеленуі екіншісіне міндетті түрде шығынсыз түсетіндей етіп орналасқан екі бет арасындағы жылулық сәулеленуді қарастырамыз. Бірінші бет абсолют қара дене және температурасы деп, ал екіншісі - жұту қабілетіне ие және температурасы деп қарастырайық.

болғанда, беттер арасында жылулық сәулелену мына түрде болады:

(13.22)

мұндағы, қара денемен толық жұтылатын сұр дененің сәулелену энергиясы; сұр денемен ішінара жұтылатын қара дененің сәулелену энергиясы. Денелердің температурасы теңескен жағдайда жылуалмасу нөлдік эффектпен жалғасып отырады:

немесе (13.23)

Алынған нәтиже барлық денелер үшін таралатын болады:

(13.24)

Барлық денелер үшін және берілген температурада абсолют қара дененің энергиясы үшін дененің сәулелендіру энергиясының қатынастары бірдей болып келеді. Бұл температура функциясы болып табылады. Егер

(13.25)

Онда (14.19)- теңдеу мынандай түрге келеді:

(13.26)

(13.27)

(14.19)-теңдеудегі Кирхгоф заңы интегралды сәулелену үшін орындалады. Бірақ монохроматты сәулелер үшін де таралады:

(13.28)

Айта кететін жағдай Кирхгоф заңы температуралық тепе-теңдік шартына негізделген. Абсолют қара денені тусіну ол сәулелік жылуалмасу теориясында үлкен рөл атқарады. Оларға мысал ретінде ашық, радиоционды және түсті температуралар жатады. Осы түсініктер мен сәулелік температуралардың функционалды байланысы жоғары температураларды өлшеу әдістерінде көрсетілген.

Дене мен қабыршық арасындағы радиоционды жылуалмасу: Алдымен екі дене арасындағы сәулелік жылуалмасуды қарастырамыз. Олардың біреуі толығымен екіншісімен қоршалған. Екі дененікі сияқты ішкі бөлшектердің жағдайы да бірдей. Екі денедегі сәулелендіру диффузиялы, дене температурасы әртүрлі. Сол себепті алдынғы есептегідей талдаймыз. Бірінші денені сәулелендіру кезіндегі бөлшектің жылу мөлшері:

(13.29)

Сонымен қатар, денемен жанасқан бөлшектің сәулеленуі кезіндегі энергиясы:

(13.30)

Егер анықтау үшін деп аламыз, онда және немесе . Температуралары тең болмаған жағдайда жылу мөлшері мына теңдікпен анықталады:

(13.31)

ескерсек, онда (14.31)-теңдеу мына түрге келеді:

,

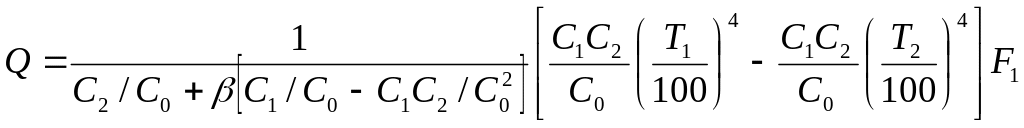(13.32)

Сәулелендіру коэффициентін баралық дәрежесіне ауыстыруға болады:

(13.33)

(13.32)

Негізгі әдебиеттер: 1 – 4.

Қосымша әдебиеттер: 1-2.

7. Семинарлық (практикалық) сабақтар жоспары (оқу жоспары бойынша жоспарланбаған)