Решение типовых примеров для контрольной работы № 2.
Задание № 1
Найти неопределенный интеграл
Решение.
Применим подстановку
,
тогда
и
;
Найти интеграл
.
Решение. Применим подставку t=3x3 – 5.
Тогда
;
,
откуда
.
Задание № 2
Найти
интеграл
Решение. Преобразуем знаменатель дроби, стоящей под знаком интеграла следующим образом:
x2 – 6x+13 = x2 – 6x + 9 + 4 = (x - 3)2 + 22. Тогда после подстановки t = x - 3 получаем
причем,
при вычислении интеграла
воспользуемся заменой переменной z
= t2+4,
тогда dz
= 2tdt,
откуда
.
Итак, учитывая, что t = x – 3, имеем
.
Задание № 3
Найти интеграл
.
Решение. Применим формулу интегрирования по частям
Положим
u = 3x+7, dv = cos5xdx,
тогда
du
= 3dx,
.
Следовательно,
.
Найти интеграл
.
Решение.
Положим
u = arctg4x, dv = dx,
тогда
v
= x.
Отсюда
.
Применяя в последнем интеграле подстановку t = 1+16x2,
получаем,
,
следовательно,
.
Отсюда
.
Задание № 4
Вычислить площадь, ограниченную параболами
y = 2x2 – x – 2,
y = - x2 + x – 1.
Решение.
Найдем абсциссы точек пересечения заданных парабол. Для этого приравняем правые части их уравнений:
2x2 – x – 2 = - x2 + x – 1. Отсюда 3x2 – 2x – 1 = 0, D = 4 + 4∙3 = 16,
Рисунок 3
,
Вычисление площади осуществляем по формуле:
,
где f1(x), f2(x) – кривые, ограничивающие фигуру (f2(x) f1(x)).
В нашем случае
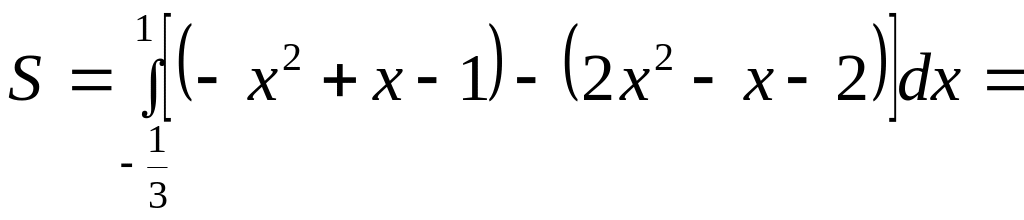
Задания к контрольной работе № 2
Задание №1
Найти неопределенные интегралы способом подстановки (методом замены переменной)
1 |
|
16 |
|
2 |
|
17 |
|
3 |
|
18 |
|
4 |
|
19 |
|
5 |
|
20 |
|
6 |
|
21 |
|
7 |
|
22 |
|
8 |
|
23 |
|
9 |
|
24 |
|
10 |
|
25 |
|
11 |
|
26 |
|
12 |
|
27 |
|
13 |
|
28 |
|
14 |
|
29 |
|
15 |
|
30 |
|
Задание №2
Найти неопределенные интегралы, используя выделение полного квадрата
1 |
|
16 |
|
|||
2 |
|
17 |
|
|||
3 |
|
18 |
|
|||
4 |
|
19 |
|
|||
5 |
|
20 |
|
|||
6 |
|
21 |
|
|||
7 |
|
22 |
|
|
||
8 |
|
23 |
|
|
||
9 |
|
24 |
|
|
||
10 |
|
25 |
|
|
||
11 |
|
26 |
|
|
||
12 |
|
27 |
|
|
||
13 |
|
28 |
|
|
||
14 |
|
29 |
|
|
||
15 |
|
30 |
|
|
||
Задание № 3
Найти неопределенные интегралы, используя метод интегрирования по частям
1 |
|
16 |
|
|
||
2 |
|
17 |
|
|
||
3 |
|
18 |
|
|
||
4 |
|
19 |
|
|
||
5 |
|
20 |
|
|
||
6 |
|
21 |
|
|
||
7 |
|
22 |
|
|
||
8 |
|
23 |
|
|
||
9 |
|
24 |
|
|
||
10 |
|
25 |
|
|||
11 |
|
26 |
|
|||
12 |
|
27 |
|
|||
13 |
|
28 |
|
|||
14 |
|
29 |
|
|||
15 |
|
30 |
|
|||
Задание № 4
Вычислить площадь, ограниченную заданными параболами
1 |
|
16 |
|
|
|||
2 |
|
17 |
|
|
|||
3 |
|
18 |
|
|
|||
4 |
|
19 |
|
|
|||
5 |
|
20 |
|
|
|||
6 |
|
21 |
|
|
|||
7 |
|
22 |
|
||||
8 |
|
23 |
|
||||
9 |
|
24 |
|
||||
10 |
|
25 |
|
||||
11 |
|
26 |
|
||||
12 |
|
27 |
|
||||
13 |
|
28 |
|
||||
14 |
|
29 |
|
||||
15 |
|
30 |
|
||||
