Министерство сельского хозяйства РФ ИНСТИТУТ АГРОЭКОЛОГИИ
– филиал ФГБОУ ВПО «Челябинской государственной агроинженерной академии»

КАФЕДРА “Механизация и электрификация сельскохозяйственного производства”

Математика методические указания

к выполнению контрольных работ

для студентов заочного отделения

Челябинск

2011

Методические указания предназначены для студентов-заочников агрономических специальностей. Указания содержат вопросы к экзамену, образцы решаемых задач, контрольные задания.

Составители:

Жаббарова М.Ж. – ассистент (кафедра «Механизация и электрификация сельскохозяйственного производства» (ГОУ Институт агроэкологии – филиал ФГОУ ВПО «ЧГАУ»))

Севостьянова Н.Н. – ст. преподаватель (кафедра «Механизация и электрификация сельскохозяйственного производства» (ГОУ Институт агроэкологии – филиал ФГБОУ ВПО «ЧГАУ»))

Рецензенты:

Рекомендованы к изданию учебно-методической комиссией Института агроэкологии – филиал ФГБОУ ВПО «ЧГАА» (протокол №__ от «___» ______2011 г.)

© Челябинская государственная агроинженерная академия, © Институт агроэкологии, 2011

Содержание

ВВЕДЕНИЕ 4

Решение типовых примеров для контрольной работы № 1 5

Задания к контрольной работе № 1 10

Решение типовых примеров для контрольной работы № 2. 18

Задания к контрольной работе № 2 20

Вопросы к экзамену 24

Приложение 25

Литература 28

Введение

Настоящее пособие предназначено для студентов заочного отделения. Пособие содержит образцы решения задач, задания для контрольных работ, вопросы к экзамену и список литературы.

При выполнении контрольных работ следует руководствоваться следующими указаниями.

1. Каждую работу следует выполнять в отдельной тетради, на обложке которой должны быть указаны фамилия и инициалы студентов, полный шифр, номер контрольной работы. Решения всех задач и пояснения к ним должны быть достаточно подробными. Все вычисления (в том числе и вспомогательные) необходимо делать полностью. Чертежи и графики должны быть выполнены аккуратно и четко с указанием масштаба, координатных осей и других элементов чертежа. Объяснения к задачам должны соответствовать тем обозначениям, которые даны на чертеже.

2. После получения работы (как зачтенной, так и незачтенной) студент должен исправить в ней все отмеченные рецензентом недостатки. В случае незачета студент обязан в кратчайший срок выполнить все требования рецензента и представить работу на повторное рецензирование, приложив при этом первоначально выполненную работу.

4. Студент выполняет тот вариант контрольных работ, который совпадает с двумя последними цифрами его учебного шифра.

Решение типовых примеров для контрольной работы № 1

Задание № 1 Вычислить пределы

1) ; 2) ,

3) , 4) .

Решение.

1) .

2) , при подстановке вместо переменной х ее предельного значения 3 получается неопределенность вида . Для избавления от этого типа неопределенности в нашем случае представим квадратные трехчлены числителя и знаменателя в виде произведения линейных множителей, воспользовавшись известной формулой

ax² + bx + c = a(x – x₁)∙(x – x₁),

где х₁, х₂ – корни квадратного трехчлена ax² + bx + c.

У нас , так как дискриминант квадратного трехчлена а следовательно, х₁ = 3, . Аналогично x² – x – 6 = (x - 3)∙(x + 2).

Теперь условие примера можно переписать в другом виде и продолжить решение:

;

3) .

Здесь сталкиваемся с неопределенностью , избавиться от которой можно вынесением за скобки в числителе и знаменателе дроби старшей степени переменной:

;

4)

В данном случае для освобождения от неопределенности будем использовать первый замечательный предел и одно из его очевидных следствий:

; .

Решение примера будет выглядеть следующим образом:

Задание № 2 Найти производные функций

1) ; 2) ;

3) ; 4) .

При решении всех последующих примеров на нахождение производных будут использованы известные правила дифференцирования суммы, разности, произведения, дроби и теорема о производной сложной функции:

а) ;

б) ;

в)

г) если задана сложная функция y = f(u), где u = (x), то есть y = f((х)); если каждая из функций y = f(u) и u = (x) дифференцируема по своему аргументу, то

Решение.

1) ,

2)

;

3)

;

4)

.

Задание № 3

Исследовать функцию и построить график

.

Решение.

1) Областью определения данной функции являются все действительные значения аргумента х, то есть

D(y): а это значит, что функция непрерывна на всей числовой прямой и ее график не имеет вертикальных асимптот.

2) Исследуем функцию на интервалы монотонности и экстремумы. С этой целью найдем ее производную и приравняем нулю:

.

Решая полученное квадратное уравнение, делаем вывод о том, что функция имеет две критические точки 1 рода х₁= - 5, х₂= - 1. Разбиваем область определения этими точками на части и по изменению знака производной в них выявляем промежутки монотонности и наличие экстремума:

х		-5	(-5, -1)	-1
	+	0	—	0	+
f(x)		max		min

.

3) Определим точки перегиба графика функции и интервалы его выпуклости и вогнутости. Для этого найдем вторую производную заданной функции и приравняем ее к нулю:

.

Итак, функция имеет одну критическую точку 2 рода х = -3;. разобьем область определения полученной точкой на части, в каждой из которых установим знак второй производной:

x		-3
	—	0 1	+
f(x)		т.п.

Значение х = - 3 является абсциссой точки перегиба графика функции, а ордината этой точки

.

4) Выясним наличие у графика заданной функции наклонных асимптот. Для определения параметров уравнения асимптоты

y = kx+b воспользуемся формулами

.

.

Таким образом, у графика заданной функции наклонных асимптот нет.

5) Для построения графика изобразим точки максимума

А₁( - 5; 4), минимума А₂( - 1 - 4), перегиба А₃(-3; 0) и точку

А₄(0; ).пересечения графика с осью Оу .

С учетом результатов предыдущих исследований построим кривую (см. рис. 2).

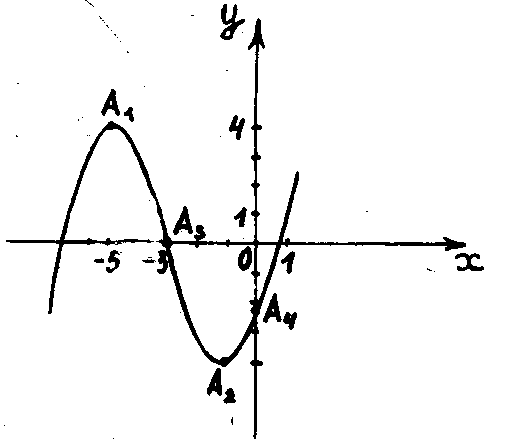
Рисунок2