3.3 Построение плана ускорений и определение линейных ускорений всех точек механизма.

Ускорение точки А

,

где - нормальное ускорение точки А, направленное от точки А к точке О;

- касательное (тангенциальное) ускорение точки А, направленное перпендикулярно ОА в сторону углового ускорения ε₁;

;

Принимаем масштабный коэффициент ускорений и находим отрезки, изображающие и :

Из полюса плана ускорений π откладываем отрезок πn₁ в направлении , а из точки n₁ – отрезок n₁а в направлении . Тогда отрезок πа изображает полное ускорение точки А:

Далее на основании теоремы о сложении ускорений в плоском движении составляем векторные уравнения в порядке присоединения структурных групп.

Для определения ускорения точки В используем уравнения

Ускорение точки B группы (2,3) находится графически из системы векторных уравнений:

,

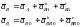
Где - нормальное и тангенциальное ускорений точки В при вращательном движении звена 2 относительно точки А,

,

(Точка В₀ неподвижна, так как принадлежит стойке);

- кориолисово ускорение точки B,

- относительное ускорение точки B по отношению к точке B₀

_{Нормальное ускорение точки В относительно точки А:}

a_BAⁿ=ω₂²∙l_AB=2.9²∙3,2=27 м/с².

Находим отрезок, изображающий a_BAⁿ:

Уравнения решаем графически. Для этого из точки а откладываем отрезок an₂ в направлении , через точку n₂ проводим линию в направлении .

Затем из полюсa π, проводим линию в направлении , т.е вертикальную прямую. В пересечении указанных линий получаем точку b

Точку S₁ центра масс кривошипа 1 строим на плане ускорений по свойству подобия посередине πа , так как l_AS1 =l_OA/2.

Точку S₂ центра масс шатуна 2 строим на плане ускорений по свойству подобия, замерив отрезок αb=100мм, и рассчитав отрезок αs₂:

αs₂= αb/3=104/3=35 мм.

Из плана ускорений находим линейные и угловые ускорения:

;

;

;

;

;

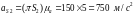Направление углового ускорения ε₂ звена 2 получим, поместив вектор тангенциального ускорения в точку В и рассматривая поворот точки В относительно точки А.

3.4 Силовой расчёт механизма

3.4.1 Определение сил инерции и моментов сил инерции звеньев

Силы тяжести звеньев:

Н;

Н;

Н;

Главные векторы сил инерции равны:

Силы инерции приложены в центрах масс и направлены противоположно ускорениям центров масс звеньев.

Главные моменты сил инерции:

;

;

Моменты сил инерции направлены противоположно угловым ускорениям звеньев.

3.4.2 Кинетостатический силовой анализ механизма

Отсоединяем группу Ассура (2,3) и строим её в масштабе μ_l=0,02м/мм.

(позиция 4 листа 1). Прикладываем к ползуну 3 внешние силы и к шатуну 2 . Действие отсоединенных звеньев 1(кривошипа) и 0(стойки) заменяем неизвестными реакциями (в точке А) и на ползуне (в точке B). Неизвестный вектор представляем как сумму

,

где - нормальная составляющая реакции ||AB

. - тангенциальная составляющая реакции , определяется из уравнения:

_{Реакцию} направим перпендикулярно направляющей ползуна 3.

_{Тангенциальную составляющую} . определим из уравнения

для звена 2:

_{Где АB, h2 и h3 – отрезки, измеренные на плане группы (2,3) в мм.}

_Тогда

Составляющая , полная реакция и реакция определяются из плана сил группы, который строится по векторному уравнению равновесия группы (2,3):

Принимаем масштабный коэффициент сил .

Отрезки сил: [1-2]= =523/30=17 мм

[2-3]= 5760/30=192 мм;

[3-4]= 75,3/30≈3мм;

[4-5]= 1336/30≈45 мм;

[5-6]= 16,5/30≈1 мм;

[6-7]= 4000/30=133 мм;

В соответствии с векторным уравнением последовательно откладываем отрезки и т.д. в направлении соответствующих сил. Затем из точки 7 проводим направление силы , а из точки 1 – направление силы . В пересечении этих направлений получаем точку 8. В результате, из плана сил находим.

=382∙30=11460H.

=383∙30=11490H.

74∙30=2220H.

Для определения реакции F₂₃ во внутреннем шарнире B рассмотрим равновесие звена 2:

Из уравнения звена 2 видно, что для определения F₂₃ достаточно на плане сил графически соединить точки 4 и 8.

193∙30=5790H.

В заключение рассматриваем начальное звено – кривошип 1. Прикладываем к кривошипу момент инерции М_и в сторону противоположную угловому ускорению ε₁. Момент уравновешивающий М_у в любую сторону. К центру тяжести прикладываем силу тяжести и силу инерции . В точке А прикладываем известную реакцию , а в точке О – реакцию со стороны стойки О, которую находим путём построения плана сил согласно уравнению равновесия:

Примем масштабный коэффициент 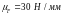. Отрезки, изображающие известные силы

мм; мм;

мм;

Откладываем отрезки … в направлении соответствующих сил, а затем, замыкая треугольник сил, соединяем точку 3 с точкой 1 отрезком [4-1]. Тогда

.

Уравновешивающий момент находим из уравнения моментов

Н·м.