1.Описание работы машины

Массы звеньев: .

_{Моменты
инерции звеньев:}

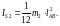
Положение центров масс звеньев l_S:

шатуна l_AS2 =l_AB/3.

_{кривошипа} l_AS1 =l_OA/2.

Схема кривошипно-ползунного механизма изображена на рисунке 1.

Таблица 1 - Исходные данные к проекту

Параметры	Обозн	Ед. изм.	Значения
Эксцентриситет	е	м	0,2
Длина кривошипа ОА		м	1.4
Длина шатуна AB		м	3.2
Угловая координата для силового рассчета		_град	60
Угол наклона цилиндров		_град	75
Угловая скорость кривошипа		с^-1	-12.57
Угловое ускорение кривошипа		с^-2	500
Сила сопротивления	_F	Н	-4000

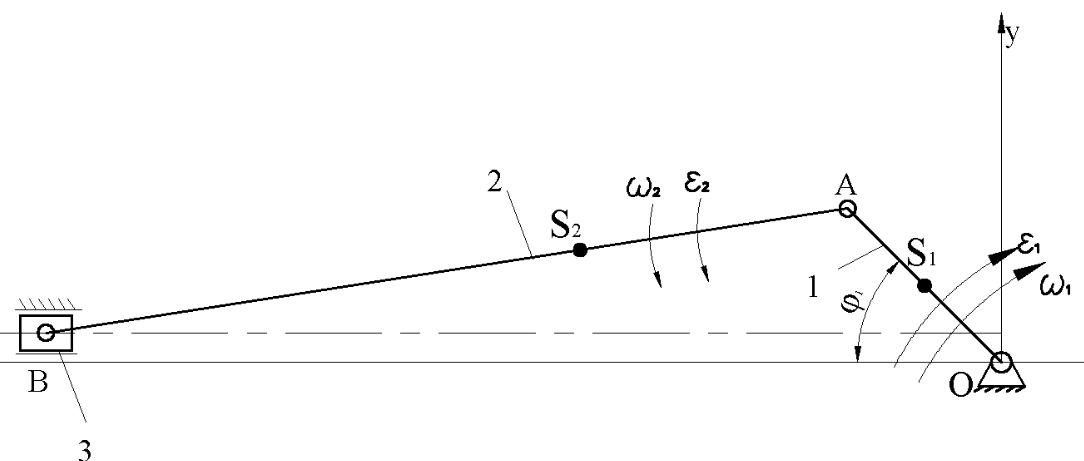
Рис 1.

2. Синтез и кинематический анализ рычажного механизма.

2.1. Структурный анализ рычажного механизма

Целью структурного анализа механизма является определение формулы строения механизма и классификация входящих в его состав структурных групп, так как формула строения определяет порядок выполнения кинематического и силового расчетов, а классы структурных групп - методы расчетов.

Структурная схема основного исполнительного механизма изображена на рис. 3.1. Число подвижных звеньев п = 3. Число низших кинематических пар p_H=4, в том числе вращательные пары - 0(1,0 ), А(1,2), В(2,3), поступательная пара В(3,0),. Число высших кинематических пар Рв ⁼0 • Число степеней свободы механизма

W=3n-2p_H-p_В=3∙3-2∙4-0=1

Рисунок.3.1

Таким образом, для того чтобы все звенья механизма совершали однозначно определенные движения, необходимо задать движение одному звену - в данном случае кривошипу 1. Тогда угловая координата кривошипа является обобщенной координатой механизма, а кривошип - начальным звеном.

Данный механизм образован последовательным присоединением к механизму 1-го класса (кривошипу 1 и стойке 0) структурной группы (2, 3) (рис. 3.2).

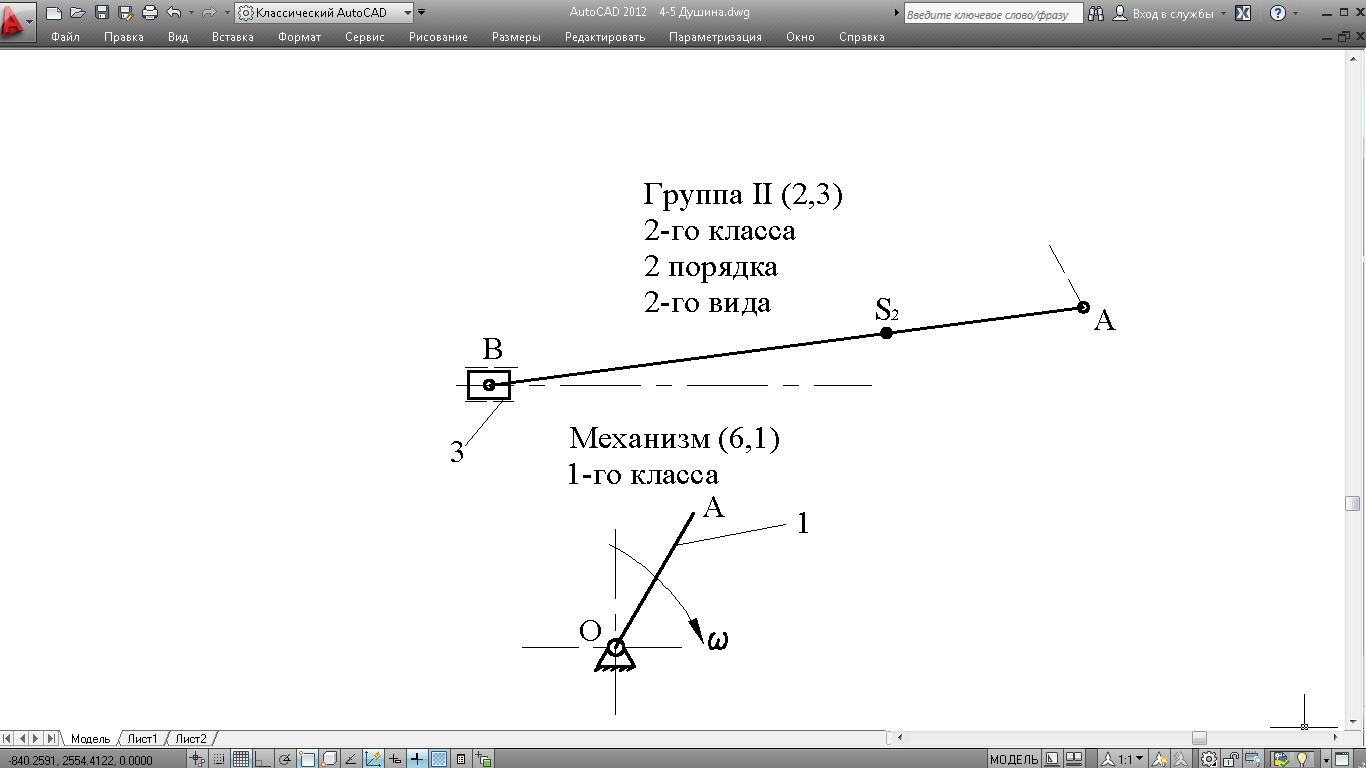
Рисунок.3.2

Формула строения механизма I(0,1)→II (2,3). Так как группа 2-го класса, то механизм относится ко 2-му классу.

Таким образом, кинематический анализ начинается с механизма I (0,1), а заканчивается группой II (2,3). Силовой расчёт выполняется в обратной последовательности II (2,3) → I (0,1).