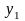5.4. Пример 1
Построить интерполяционный многочлен Лагранжа для следующей заданной таблично функции :
x |
0.75 |
1.50 |
2.25 |
3.00 |
3.75 |
y |
2.50 |
1.20 |
1.12 |
2.25 |
4.28 |
Если
имеется пять значений функции в заданных
точках, то интерполяционный многочлен
мы получим четвертой степени, имеющим
вид:
,
где
сами являются так же многочленами
четвертой степени от x.
Вот как они получаются:
Сам интерполяционный многочлен имеет вид:
5.5. Пример 2
Найти с помощью метода наименьших квадратов аппроксимирующий многочлен для следующей таблично заданной функции , приняв предположение, что является линейной:
x |
0.75 |
1.50 |
2.25 |
3.00 |
3.75 |
y |
2.50 |
1.20 |
1.12 |
2.25 |
4.28 |
Т.к. исходная функция предполагается линейной, то в качестве аппроксимирующего многочлена выберем многочлен первой степени вида:
.
Тогда
.
Система линейных уравнений для поиска
параметров
будет иметь следующий вид:
,
где значения коэффициентов при неизвестных параметрах равны:
Получаем
систему
,
решая которую методом Гаусса получаем
.
Следовательно,
функция, аппроксимирующая заданную
табличную
,
имеет вид:
.
5.6. Пример 3
Найти с помощью метода наименьших квадратов аппроксимирующий многочлен для той же таблично заданной функции, что и в предыдущем примере, но, приняв предположение, что зависимость является квадратичной.
x |
0.75 |
1.50 |
2.25 |
3.00 |
3.75 |
y |
2.50 |
1.20 |
1.12 |
2.25 |
4.28 |
Т.к. исходная функция предполагается квадратичной, то в качестве аппроксимирующего многочлена выберем многочлен второй степени вида:
.
Тогда
и система линейных уравнений для поиска
параметров
будет иметь следующий вид:
,
где значения коэффициентов при неизвестных параметрах равны:
Система уравнений запишется в виде:
Решение
этой системы методом Гаусса даст
следующие значения параметров:
.
Следовательно,
аппроксимирующая функция имеет вид
.
5.7 Упражнения для самостоятельного решения
Определение коэффициентов функциональной зависимости с помощью метода наименьших квадратов
5.7.1. Задача №1
При
пяти различных значениях температуры
было
измерено напряжение сдвига
.
Найти коэффициенты функциональной
зависимости напряжения сдвига от
температуры при двух различных
предположениях о характере этой
зависимости: предполагая в первый раз,
что эта зависимость имеет линейный
характер, т.е.
,
и второй раз, что она имеет квадратичный характер
.
В таблице в каждой строке даны пять значений напряжения сдвига, отвечающих следующим значениям температуры:
(в
градусах Цельсия).
№ вар. |
Значение
|
||||
|
|
|
|
|
|
1 |
14 |
16 |
20 |
26 |
44 |
2 |
15 |
17 |
20 |
26 |
45 |
3 |
16 |
18 |
21 |
28 |
46 |
4 |
16 |
17 |
20 |
26 |
44 |
5 |
13 |
17 |
20 |
26 |
45 |
6 |
15 |
18 |
21 |
28 |
46 |
7 |
14 |
17 |
20 |
26 |
44 |
8 |
15 |
18 |
20 |
26 |
45 |
9 |
16 |
19 |
21 |
28 |
46 |
10 |
14 |
16 |
21 |
26 |
44 |
11 |
15 |
17 |
22 |
26 |
45 |
12 |
16 |
18 |
23 |
28 |
46 |
13 |
14 |
16 |
20 |
25 |
44 |
14 |
15 |
17 |
20 |
26 |
45 |
15 |
16 |
18 |
21 |
27 |
46 |
16 |
14 |
16 |
20 |
26 |
43 |
17 |
15 |
17 |
20 |
26 |
44 |
18 |
16 |
18 |
21 |
28 |
45 |
19 |
14 |
16 |
20 |
24 |
44 |
20 |
15 |
17 |
21 |
26 |
45 |
21 |
16 |
17 |
21 |
28 |
46 |
22 |
13 |
16 |
20 |
26 |
44 |
23 |
15 |
16 |
22 |
27 |
45 |
24 |
16 |
18 |
21 |
28 |
47 |
º
º
º
º
º
