2.2. Метод хорд

Этим методом можно пользоваться в том случае, если функция непрерывна в некоторой окрестности корня уравнения.

Для начала ищется отрезок в этой окрестности, который содержал бы только один искомый корень уравнения, а значения функции на концах его были бы разных знаков. Так как функция непрерывна на этом отрезке, то ее график обязательно где-то внутри этого отрезка пересечет ось абсцисс. Эту точку х пересечения графика функции с осью ОХ, являющуюся корнем уравнения, и нужно найти.

Затем строится хорда, соединяющая точки графика функции, отвечающие концам имеющегося отрезка. Вычисляется точка пересечения этой хорды с осью ОХ. Назовем эту точку х₁. Затем определяется, на каком из отрезков или лежит корень уравнения. Если 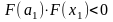, то корень лежит на отрезке и становится правым концом нового (уже меньшего) отрезка локализации корня, а – левым концом этого отрезка. При этом производят переименование и .

Если , то корень – на отрезке и становится левым концом нового отрезка локализации корня, а – правым концом этого отрезка, т.е. и .

Теперь имеется уже новый отрезок локализации корня. С ним проделывается та же процедура построения хорды и поиска точки ее пересечения с осью ОХ – точки . Остановка производится при нахождении отрезка , длина которого не больше . Тогда в качестве корня берут середину этого отрезка.

Этот процесс можно увидеть на рис.1.

Рис.1

Формула для получения точки пересечения хорды с осью ОХ на каждом шаге имеет следующий вид:

2.2. Метод касательных Ньютона

Этот метод можно использовать в случае выполнения следующих требований к функции :

На найденном отрезке локализации корня должна иметь единственный корень и значения функции на концах этого отрезка должны быть разных знаков, т.е. .
должна иметь непрерывную вторую производную на этом отрезке.
Кроме того, на отрезке вторая производная функции

должна сохранять свой знак.

Тогда в качестве начального приближения корня выбирается по следующему правилу:

Затем в точке с абсциссой строится касательная к графику функции . Точка пересечения этой касательной с осью ОХ берется в качестве следующего приближения корня . И так процесс продолжается до тех пор, пока не будет достигнута нужная точность .

Если достаточно получить точку, в которой не превышает по модулю заданное число , то производят остановку при выполнении этого условия.

Если же надо получить приближение корня, отстоящее от истинного его значения не более чем на , то процесс останавливают тогда, когда выполняется следующее условие:

, где