
- •Погрешности вычислений
- •1.1. Основные определения и свойства
- •1.2. Пример
- •Упражнения для самостоятельного решения
- •2. Методы решения нелинейных уравнений
- •2.1. Общие сведения
- •2.2. Метод хорд
- •2.2. Метод касательных Ньютона
- •2.3. Пример 1
- •2.4. Пример 2
- •2.5. Упражнения для самостоятельного решения:
- •3. Методы решения систем линейных уравнений
- •3.1. Основные понятия
- •3.2. Метод Гаусса
- •3.3. Итерационные методы
- •3.4. Пример 1
- •3.5. Пример 2
- •3.6. Упражнения для самостоятельного решения
- •5. Интерполяция и аппроксимация функции
- •5.1. Основные определения
- •5.2. Интерполяция функции
- •5.3. Аппроксимация функции
- •5.4. Пример 1
- •5.5. Пример 2
- •5.6. Пример 3
- •5.7 Упражнения для самостоятельного решения
- •5.7.1. Задача №1
- •5.8. Упражнения для самостоятельного решения
- •5.8.1. Задача №1
- •6. Численное интегрирование
- •6.1. Основные определения
- •6.2. Метод прямоугольников.
- •6.3. Метод трапеций
- •6.4. Метод Симпсона
- •6.9. Упражнения для самостоятельного решения
- •6.9.1. Задача №1
- •7. Методы решения задачи Коши для обыкновенных дифференциальных уравнений 1-го порядка
- •7.1. Основные понятия
- •7.2. Метод Эйлера
- •7.3. Модифицированный метод Эйлера
- •7.4. Метод Рунге-Кутта
- •7.5. Пример 1
- •7.6. Пример 2
- •7.8. Пример 3
- •7.9. Упражнения для самостоятельного решения
- •7.9.1. Задача №1
- •7.10. Упражнения для самостоятельного решения
- •7.10.1. Задача №1
- •7.10.2. Задача №2
7.8. Пример 3
Решить ту же задачу методом Рунге-Кутта:
Запишем формулы метода Рунге-Кутта:
, где
Проведем по ним расчеты.
Для
 имеем
имеем


Для
 имеем
имеем
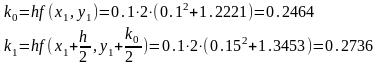


………………………………………………………………..
Для
 имеем
имеем


Выпишем полученные по методу Рунге-Кутта значения функции и значения точного решения в этих же точках в таблицу и проследим накопление ошибки:
|
Метод Рунге-Кутта |
Точное решение |
Ошибка вычислений |
|
1.2221 |
1.2221 |
0.0000 |
|
1.4977 |
1.4977 |
0.0000 |
|
1.8432 |
1.8432 |
0.0000 |
|
2.2783 |
2.2783 |
0.0000 |
|
2.8274 |
2.8274 |
0.0000 |
|
Метод Рунге-Кутта |
Точное решение |
Ошибка вычислений |
|
3.5201 |
3.5202 |
0.0001 |
|
4.3927 |
4.3928 |
0.0001 |
|
5.4894 |
5.4895 |
0.0001 |
|
6.8643 |
6.8645 |
0.0002 |
|
8.5834 |
8.5836 |
0.0002 |
Сравнивая картину погрешностей в методе Рунге-Кутта и в рассмотренных ранее методе Эйлера и модифицированном методе Эйлера, можно видеть, что погрешности этого метода на несколько порядков меньше соответствующих погрешностей двух других методов. Именно поэтому метод Рунге-Кутта находит наибольшее применение.
7.9. Упражнения для самостоятельного решения
Решение задачи Коши для дифференциального уравнения первого порядка методом Эйлера
7.9.1. Задача №1
Степень
радиоактивности пропорциональна
количеству остающегося вещества. Можно
написать дифференциальное уравнение,
отображающее скорость изменения
количества радиоактивного вещества:
 ,
где y
– это
количество вещества в момент времени
t.
Пусть k=0.01
и количество вещества, имеющегося на
момент времени t0=0
равно y0=100
г. Требуется найти количество вещества,
которое останется на момент времени
t=100.
,
где y
– это
количество вещества в момент времени
t.
Пусть k=0.01
и количество вещества, имеющегося на
момент времени t0=0
равно y0=100
г. Требуется найти количество вещества,
которое останется на момент времени
t=100.
Эта задача проста с точки зрения математики, и для нее можно указать аналитическое решение. Оно имеет следующий вид:
 ,
так что при t=100
получаем y(100)=36.788
г
,
так что при t=100
получаем y(100)=36.788
г
Это точное решение поможет нам сравнить работу разных методов и проследить накопление ошибки при подсчете значения y(100).
Решите задачу по данным своего варианта (указанным методом и с заданным шагом) и сравните значение y(100) с точным значением.
Данные по вариантам:
№ вар. |
1
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Ме-тод |
Эйле-ра |
Эйле-ра |
Эйле-ра |
Эйле-ра |
Моди-фици-рован-ный Эйле-ра |
Моди-фици-рован-ный Эйле-ра |
Рунге-Кутта |
Рунге-Кутта |
h |
25 |
10 |
5 |
1 |
20 |
10 |
100 |
50 |
7.10. Упражнения для самостоятельного решения
Решение задачи Коши для дифференциального уравнения первого порядка методом Рунге-Кутта
