1.4 Проекции силы на ось и на плоскость
Проекцией силы на ось называют скалярную величину, равную, взятой с соответствующим знаком, длине отрезка, заключенною между проекциями начала и конца вектора силы на эту ось.
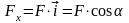
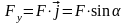
Проекция силы на ось равна произведению модуля силы на косинус угла между направлением силы и положительным направлением оси.
Проекция
будет положительной если угол α
острый; отрицательной – α
тупой. Если сила
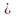к оси, то проекция равна 0.
Проекцией
силы на плоскость Oxy
называется вектор Fxy,
заключенный между проекциями начала и
конца вектора силы
на эту плоскость.
;
;
;
.
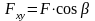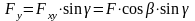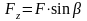1.4. Условия равновесия системы сходящихся сил. Теорема о равновесии трех непараллельных сил
Силы, линии действия которых пересекаются в одной точке, образуют систему сходящихся сил.
Пусть
задана система сходящихся сил (рис. 1.3)
,
,...
.
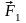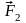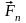Рис. 1.3
Равнодействующая система сходящихся сил равна векторной сумме всех сил системы и проходит через точку пересечения их линий действия.
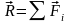
Проекции равнодействующей системы сходящихся сил на координатные оси равны алгебраической сумме проекций всех сил системы на соответствующие оси.
,
,
.
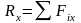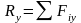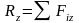Вычислив проекции равнодействующей, можно определить ее модуль и направляющие косинусы:
;
;
;
.
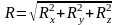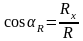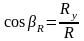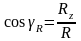где αR, βR и γR – углы, образуемые равнодействующей с осями x, y и z соответственно.
При равновесии системы сходящихся сил R=0 и сумма проекций всех сил системы на три координатные оси равна нулю.
;
;
;
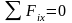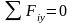Для системы сходящихся сил, расположенных в одной плоскости, получаем два уравнения равновесия:
; .
Если тело находится в равновесии под действием трех непараллельных сил, то эти силы лежат в одной плоскости и линии их действия пересекаются в одной точке.
Задача
Груз удерживается в равновесии двумя стержнями АС и ВС, шарнирно соединенными в точках А, В и С. Стержень ВС растянут силой F2 = 45 Н, а стержень АС сжат силой F1 = 17 Н. Определить вес груза, если заданы углы α = 15º и β = 60º.
______________________________________
Решение:
Шарнир
С
находится в равновесии под действием
плоской системы сходящихся сил:
.
Составим
уравнение равновесия:
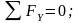
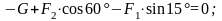
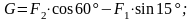
Подставляя
значения сил получим
Н.
Ответ: G = 18,1 Н.
1.5 Момент силы относительно точки
Момент
силы относительно точки (центра)
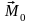– вектор, численно равный:
.
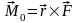Направление вектора перпендикулярно плоскости, проходящей через выбранную точку и линию действия силы в ту сторону, откуда «вращение», совершаемое силой вокруг точки, наблюдается происходящим против хода часовой стрелки (рис. 1.4).
Рис.1.4
Плечо силы h – кратчайшее расстояние от точки 0 до линии действия силы F (рис. 1.4).
На плоскости моментом силы относительно точки O считают положительным, если сила стремится вращать тело против хода часовой стрелки, в обратном – отрицательным.
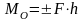
Задача
На плиту в ее плоскости действует две пары сил. Определить сумму моментов этих пар, если сила F = 8 Н, Q = 5 Н, расстояния АВ = 0,25 м, CD = 0,20 м, углы α = 60º и β = 70º.
________________________________
Решение:
Составим уравнение равновесия:
Н∙м.
Ответ: ΣМ = 0,79 Н∙м.