Решение

Взаимная индуктивность

,

где Ф – магнитный поток, пронизывающий рамку

.

Элементарный магнитный поток, пронизывающий площадку ,

.

Магнитная индукция B за пределами проводника с током (см. задачу 13.1)

.

Тогда

и

 Гн.

Задача 13.9

Н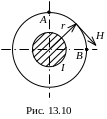 айти разность скалярных магнитных потенциалов между точками A и B, расположенными в магнитном поле линейного тока.  А,  см (рис. 13.10).

Решение

.

Напряженность поля H на расстоянии r от линейного тока (см. задачу 13.1)

.

Тогда

А.

Задача 13.10

Индуктивность однослойной короткой катушки на низкой частоте приближенно определяется выражение

 Гн,

где r – радиус витков, l – длина катушки, w – число витков.

Определить силу, стремящуюся сжать катушку, и силу, стремящуюся разорвать витки катушки, при токе  А, если  м,  м, .

Решение

Сила определяется как частная производная энергии поля по координате перемещения

.

Сила, стремящаяся уменьшить размер l (сжать катушку):

 Н.

Сила, стремящаяся разорвать витки катушки:

 Н.

Задача 13.11

П олый шар с радиусом стенок и , выполненный из материала с относительной магнитной проницаемостью , помещен во внешнее однородное магнитное поле с индукцией (рис. 13.11). Определить индукцию B в полости шара, если .

Решение

Экранирующее действие шара определяется тем, что линии магнитной индукции внешнего поля, стремясь пройти по пути с наименьшим магнитным сопротивлением, сгущаются внутри стенок экрана, почти не проникая в его полость.

Величина индукции в полости шара [2]

,

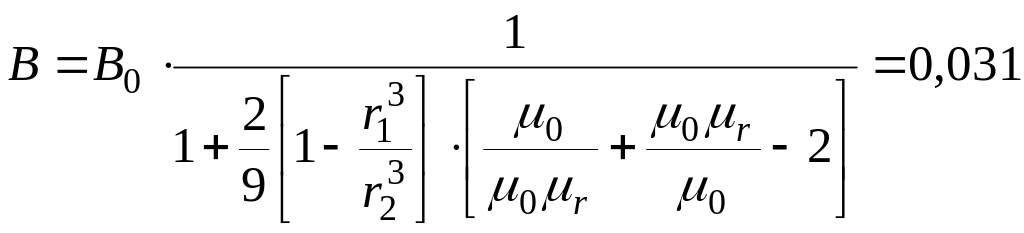
т.е. индукция внутри экрана составляет 3% от индукции внешнего поля.

Задача 13.12

Цилиндрический экран с радиусами стенок см, см, выполненный из материала с относительной магнитной проницаемостью , помещен во внешнее магнитное поле напряженностью (рис. 13.12). Определить напряженность поля во внутренней полости цилиндра.

Решение

Напряженность внутри цилиндра может быть приближенно рассчитана по формуле [3]

,

т.е. напряженность поля внутри экрана составляет всего 0,23% от напряженности внешнего поля.

Задача 13.13

Внутри длинной многослойной цилиндрической катушки расположен соосно магнитомягкий ферритовый цилиндрический сердечник (рис. 13.13). Известны геометрические размеры , , , ; число витков катушки w; магнитная проницаемость сердечника (  Гн/м – магнитная проницаемость вакуума).

Рассчитать приближенно индуктивность катушки с сердечником.

Общие сведения

Потокосцепление катушки с сердечником представим в виде суммы

,

г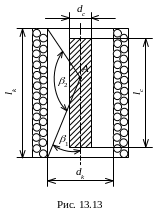 де – потокосцепление катушки с током без сердечника, – приращение потокосцепления катушки, обусловленное намагниченностью сердечника J. Тогда

,

где – индуктивность катушки без сердечника,

– приращение индуктивности катушки за счет увеличения потокосцепления, обусловленного намагниченностью сердечника.

Решение

1. Рассчитаем . Так как катушка длинная, приближенно можно считать, что магнитное поле внутри катушки однородно, а векторы напряженности и индукции направлены вдоль оси катушки и имеют значения

,

.

Эти выражения вытекают из закона полного тока в предположении, что выполняется условие: .

Тогда

,

где – магнитный поток, с которым, будем считать, сцепляются все витки катушки (такое допущение является приближенным). Расчет по этой приближенной формуле дает несколько завышенное значение индуктивности. Более точный расчет и в центре соленоида (точка А на рис. 13.13) дает формула [3]

,

которая при и имеет вид

.

Последняя формула была использована выше.

2. Рассчитаем . Для приближенного расчета цилиндрический сердечник заменим эллипсоидом вращения (показан пунктиром на рис. 158), длинная полуось его равна , которая равна . Известно, что эллипсоид вращения в однородном магнитном поле намагничивается однородно, т.е. результирующее магнитное поле внутри него имеет одно и то же значение индукции, которое пропорционально внешнему полю (в данном случае полю ). Тогда, используя теорему о потоке [5], можно записать

.

Для случая эллипсоида вращения ( ) в однородном поле [5]

,

где N – коэффициент размагничивания, – относительная магнитная проницаемость сердечника ( ).

Коэффициент N рассчитывается по формуле [6]

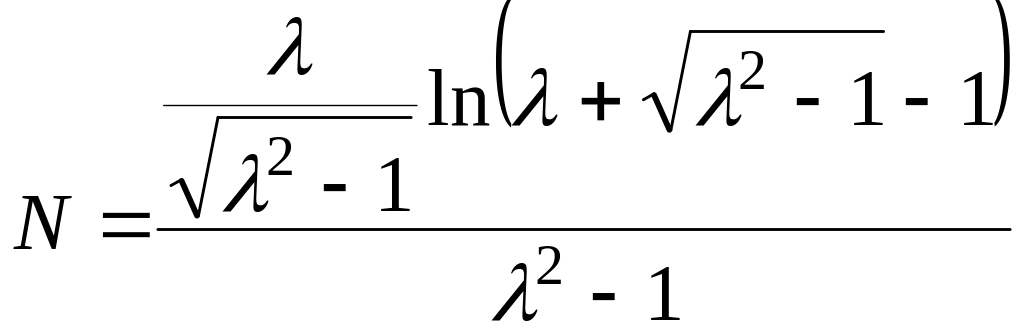, (13.18)

где .

Следовательно,

.

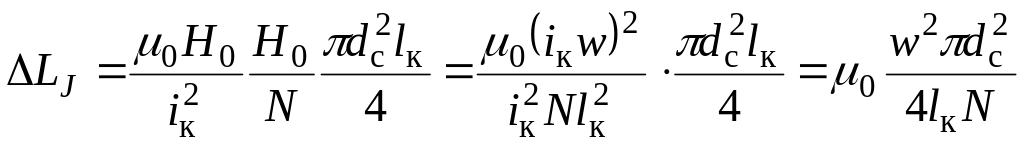Таким образом,

. (13.19)

Пусть мм, мм, , мм, мм. Для данного соотношения из (13.18) получаем . Расчет по формуле (13.19) дает следующий результат:

Гн.

Как видно из результатов расчета, введение сердечника в катушку увеличивает ее индуктивность почти в шесть раз.

Задача 13.14

Определить заряд Земли Q. Радиус Земли  км, напряженность у поверхности Земли  В/см.