Глава 13

МАГНИТНОЕ ПОЛЕ ПОСТОЯННОГО ТОКА

Теоретические положения

Закон полного тока:

. (13.1)

Закон Био-Савара:

. (13.2)

Закон Ампера:

. (13.3)

Зависимость между магнитной индукцией и напряженностью магнитного поля (изотропные среды):

, (13.4)

где  Гн/м – магнитная постоянная;

– относительная магнитная проницаемость.

Интенсивность намагничивания:

, (13.5)

где – относительная магнитная восприимчивость.

Первое уравнение Максвелла для постоянных токов:

(13.6)

где – абсолютная магнитная проницаемость.

Зависимость между напряженностью магнитного поля и векторным потенциалом:

(13.7)

Векторный потенциал магнитного поля:

. (13.8)

Основные уравнения магнитного поля:

(13.9)

Граничные условия в магнитном поле:

(13.10)

где – поверхностная плотность тока.

Энергия магнитного поля:

. (13.11)

Магнитный поток:

. (13.12)

Соленоидальность магнитного поля:

(13.13)

Векторный потенциал линейного тока:

. (13.14)

Примеры решения задач

Задача 13.1

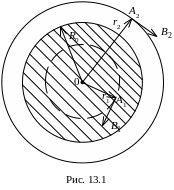
По неограниченно длинному стальному проводнику (рис. 13.1) радиусом  мм с относительной магнитной проницаемостью течет ток  А.

Определить магнитную индукцию в точках и , находящихся соответственно на расстоянии от оси проводника  мм и  мм.

Решение

Используя закон полного тока в интегральной форме

,

и учитывая, что на окружности радиусом r, получаем

, .

Отсюда индукция

,

здесь – ток, охватываемый контуром интегрирования.

Для точки , расположенной внутри проводника,

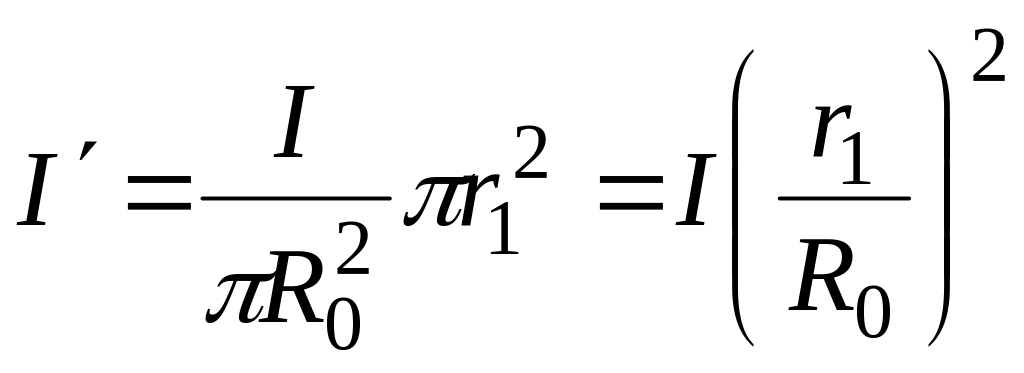
и

 Тл.

Для точки , расположенной вне проводника, величина . Учитывая, что у воздуха , получаем

Тл.

Задача 13.2

В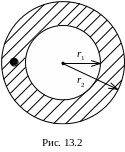 доль стальной трубы ( ) с внутренним радиусом  см и наружным  см течет постоянный ток  А (рис. 13.2). Построить график зависимости напряженности магнитного поля H на расстоянии r от оси трубы.

Решение

Выведем формулы для определения напряженности поля H во внутренней полости трубы, в теле трубы и снаружи трубы, для чего воспользуемся законом полного тока в интегральной форме:

,

где – ток, охваченный контуром интегрирования.

Учитывая, что на окружности радиусом r с центром на оси трубы, получим

, .

Окружность радиуса не охватывает тока, поэтому во внутренней полости трубы магнитное поле отсутствует .

Контур интегрирования радиусом охватывает ток

,

где – площадь поперечного сечения трубы,

– площадь с током, охваченная контуром интегрирования.

Тогда

.

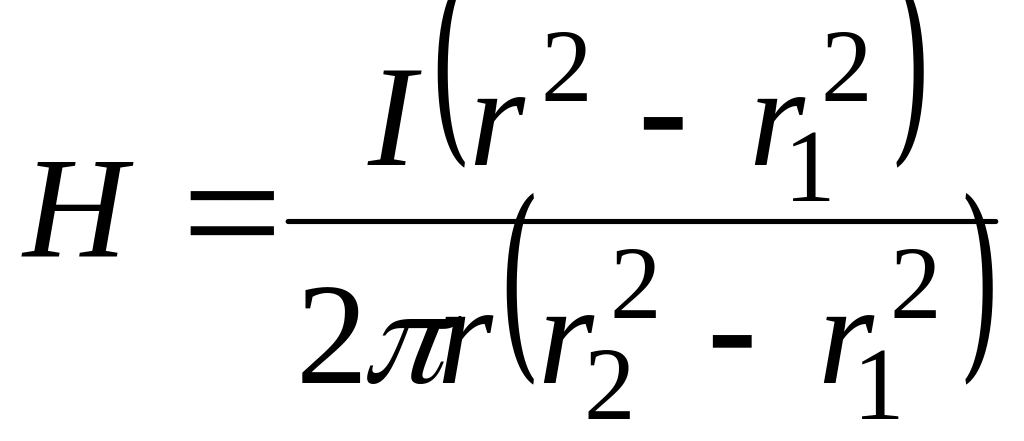Снаружи трубы ( ) контур интегрирования охватывает ток и напряженность поля убывает по гиперболическому закону

.

Максимальное значение напряженности имеет место на внешней поверхности трубы:

 А/м.

График распределения напряженности приведен на рис. 13.3.

Задача 13.3

П ровод с постоянным током  А находится на оси стальной трубы с относительной магнитной проницаемостью . Радиус провода  см. Внутренний радиус трубы  см, внешний радиус  см (рис. 13.4).

Определить напряженность и магнитную индукцию в точках  см, 4,5 см.