Любые совпадения имен в приведенном примере – случайны! Претензии к автору книги.
Кандидатуры характеризуются множеством значений параметров, например:
Критерий |
Кандидатуры |
|||
Маша |
Даша |
Глаша |
… |
|
Ум (уровень интеллекта), баллов |
7 |
5 |
3 |
… |
Красота, баллов |
4 |
6 |
7 |
… |
Рост, см |
170 |
155 |
162 |
… |
Вес, кг |
60 |
72 |
51 |
… |
… |
… |
… |
… |
… |
Для быстрой приближенной оценки ограничимся двумя параметрами – умом и красотой. Тогда все кандидатуры могут быть представлены точками в двумерном пространстве.
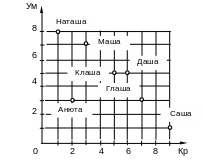
Видно, что кандидатуры с предельно высоким значением одного параметра имеют явно нежелательные значения по второму параметру. Требуется найти компромисс.
Для выбора конкретной кандидатуры могут быть использованы такие методы:
1. Выбрать один параметр в качестве критерия, а второй ограничить минимально допустимым значением (Метод главного критерия). Например, основной критерий – ум, минимальный балл по красоте – 5.
Решение: требуется найти в области допустимых решений точку с максимальным баллом по интеллекту и с показателем красоты не менее 5. Оптимальный вариант – Даша.
2. Установить количественное соотношение между значениями параметров (Метод скаляризации). Например, если по мнению потенциального жениха, ум вдвое ценнее, чем красота, то нужно обеспечить максимальное значение выражения (2 Ум + 1 Кр) max . (2 и 1 – это и есть весовые коэффициенты.)
Р
ешение:
Маша – взвешенная сумма баллов 18,
Наташа – 17, Даша – 16 и т.д.
3. Сокращение множества вариантов путем исключения явно бесперспективных (Множество Парето). Так, Анюта уступает Глаше, которая при том же уровне интеллекта красивее, по тем же причинам Даша перспективнее, чем Клаша.
Остаются только претендентки, характеризуемые крайними точками области – Наташа, Маша, Даша, Глаша, Саша. (Это и есть множество Парето.) Эти кандидатуры следует предложить лицу, принимающему решение (ЛПР, т.е. жениху), а дальше пусть он выбирает сам, руководствуясь неформальными соображениями.
Пример2 (Метод последовательной оптимизации): Многокритериальная оптимизация при формировании облика самолета [Егер и др. Основы автоматизированного проектирования самолетов, с. 134-137]:
Варианты конструкции самолета-истребителя, которые различаются площадью крыла, углом его стреловидности, удлинением и сужением, длиной средней части фюзеляжа и диаметром двигателя, обладают различными значениями взлетной массы и основных летных характеристик:
Критерии |
Вариант |
|||
1 |
2 |
3 |
... |
|
Скороподъемность, м/с |
315 |
331 |
312 |
... |
Максимальная угловая скорость разворота, град/с |
25.9 |
25.3 |
26.7 |
... |
Время разгона от 600 до 1300 км/ч, с |
18.0 |
17.0 |
18.1 |
... |
Взлетная масса, кг |
17691 |
18607 |
18780 |
... |
Подобные задачи также могли бы решаться с использованием весовых коэффициентов, однако в проектировании таких сложных объектов, как самолет, это не всегда допустимо.
[Там же, с.69]: В практических задачах далеко не всегда удается найти обобщенный показатель качества, включающий в себя частные критерии. В таких случаях возникает задача многокритериальной (векторной) оптимизации. Для многокритериальной задачи решение в общем случае не является оптимальным ни по одному из частных критериев. В то же время оно является компромиссным для векторного критерия
F = [f1, .. , fm] .
В этой же работе (с. 117-123) рассмотрен эффективный метод понижения размерности вектора конструктивных параметров – построение иерархии проектных задач и переход к последовательной оптимизации при формировании облика самолета. Взамен совместного рассмотрения 31 переменной выполняется последовательное решение задач оптимизации на следующих 5 уровнях:
1. Оптимизация геометрических параметров крыла и размеров двигателя.
2. Оптимизация геометрических и конструктивных параметров фюзеляжа и крыла (в части их взаимного расположения).
3. Оптимизация геометрических параметров горизонтального оперения.
4. Оптимизация геометрических параметров вертикального оперения.
5. Оптимизация силовой установки (согласование планера с двигателем).
Более подробное описание методов и математических моделей принятия решений при наличии многих критериев приведено, например, в работе [Разработка САПР. В 10 кн. Кн.2. Системотехнические задачи создания САПР / А.Н.Данчул, Л.Я.Полуян. Под ред. А.В.Петрова. 1990]
В работе [Перегудов, Тарасенко. Введение в системный анализ] описаны также методы принятия решений с использованием бинарных отношений и функций выбора, основанные не на количественной оценке отдельных альтернатив (что зачастую невозможно), а на их попарном сравнении, т.е. на ранговой оценке.