
- •Тема 3. Задачи многокритериальной оптимизации
- •1. Многокритериальная оптимизация
- •2. Определение множества Парето
- •Выбор критерия оптимальности.
- •Любые совпадения имен в приведенном примере – случайны! Претензии к автору книги.
- •Решение задач многокритериальной оптимизации с использованием генетических алгоритмов Matlab Optimtool
|
Кафедра информационных технологий проектирования летательных аппаратов |
Конспект лекций: СОВРЕМЕННЫЕ МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ ПРОЕКТИРОВАНИЯ |
|
Тема 3. Задачи многокритериальной оптимизации
Учебные вопросы:
Многокритериальная оптимизация.
Определение множества Парето.
Выбор критерия оптимальности.
Методы условной многокритериальной оптимизации
Генетические алгоритмы.
1. Многокритериальная оптимизация
На предыдущих лекциях мы рассмотрели задачи, в которых требуется выбрать решение, имеющее максимум (или минимум) единственного показателя эффективности (критерия) k. На практике часто возникает случай, когда эффективность проектируемого изделия приходится оценивать не по одному, а сразу по нескольким показателям k1 ,k2 ,…,kL.
Примеры:
1. Оценка деятельности завода: прибыль, средняя зарплата, объем производственных фондов.
2. Оценка учебы студента: оценки по предметам, посещаемость.
Одни из этих показателей необходимо сделать больше, другие меньше. Главной особенностью этой ситуации является то, что требования ко всем показателям в реальных системах несовместимы или противоречивы.
Для удобства сравнения значений векторов k=(k1, k2, … kL) – иногда удобно предварительно привести все показатели k1 , k2… kL к стандартному виду, чтобы все критерии минимизировались и чтобы они имели безразмерный масштаб измерения. Стандартный критерий (нормированный) можно задать в виде отношения: kст i=(1 – ki / kи i), где kи i – идеальное значение критерия (либо определенное значение, либо max ki)
При этом в L-мерном пространстве задаётся вектор k, каждая компонента которого изменяется от 0 до 1. Полностью идеальной системе соответствует k=0.
Прежде всего, анализ векторов, соответствующих альтернативам из области допустимых альтернатив, позволяет заранее отбросить явно нерациональные варианты решений, уступающие лучшим вариантам по всем показателям. Этот этап векторной оптимизации называется безусловной оптимизацией.
Пусть анализируется боевая операция, оцениваемая по двум показателям.
k1 – вероятность выполнения боевой задачи;
k2 – стоимость израсходованных средств.
Очевидно, первый из показателей желательно обратить в максимум, а второй в минимум. Пусть предлагается на выбор конечное число различных вариантов решения, обозначим их X1, X2, ..., Xn. Для каждого известны значения k1, k2 . Изобразим каждый вариант решения в виде точки на плоскости с координатами k1, k2. Когда X принимают значения из области допустимых решений (ОДР), точки k1, k2 заполняют критериальное пространство решений (Рис. 5.1).
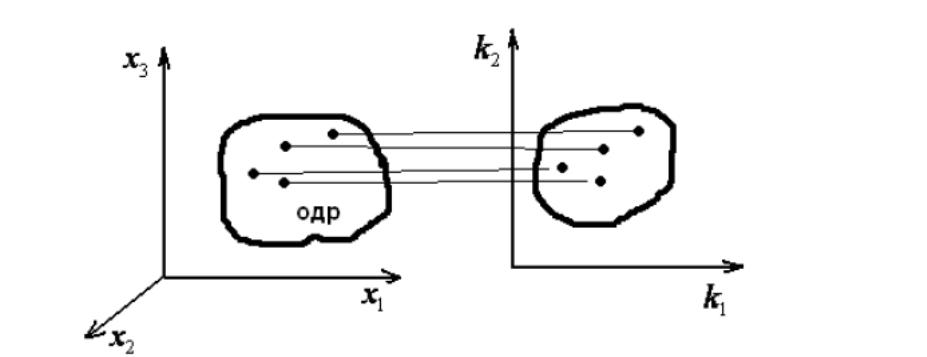 Рис.
5.1
Рис.
5.1
Итак, если некоторая операция оценивается несколькими критериями, то такая задача называется задачей многокритериальной или векторной оптимизации. Для стандартных k эта задача имеет вид
![]() (5.1)
(5.1)
![]() (5.2)
(5.2)
Существует принципиальная трудность в объективной (безусловной) оценке альтернатив при двух или более критериях. Она связана с проблемой сравнения двух векторов.
Безусловным критерием предпочтения называют критерий, основанный на сравнении компонент вектора. Два вектора критериев kA и kB безусловно сравнимы , если для любой l-й компоненты вектора выполняются неравенства
![]()
Если все kl→ min, то альтернатива B безусловно предпочтительнее (лучше) A. Это означает, что А никак не может быть оптимальной и поэтому должна быть отброшена. Если же знаки неравенств для различных компонент вектора различны, то такие альтернативы безусловно несравнимы. Рассмотрим пример.
Необходимо выбрать лучших по успеваемости студентов А, Б, В, Г, Д. Критериями служат оценки по предметам М, N, O, P.
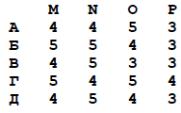
Проведем безусловное сравнение векторов оценок. Студент А не сравним с Б. В безусловно хуже Б – отбросим В. Д безусловно хуже Б – отбросим Д. А безусловно хуже Г – отбросим А. Остались две альтернативы Б и Г, которые безусловно несравнимы.
Определение. Множество безусловно несравнимых альтернатив, оставшихся после отбрасывания всех безусловно худших альтернатив, называется множеством Парето. Парето-оптимальное множество еще называют областью компромиссов. Ясно, что множество Парето можно получить в результате анализа критериального пространства.
Таким образом многокритериальная оптимизация включает два этапа.
1.Безусловная оптимизация. Здесь анализируется критериальное пространство, отсеиваются безусловно худшие варианты и получают множество Парето
2. Условная оптимизация. Так как множество Парето, как правило, состоит из более чем одной точки, то для получения единственного решения необходимо применить дополнительные принципы оптимальности (условия согласования критериев).

