Вопрос20.Производная обратной и сложной функций.

Пусть - дифференцируемая функция от аргумента x в некотором интервале . Если в уравнении y считать аргументом, а x - функцией, то возникает новая функция , где - функция обратная данной. Теорема (о дифференцировании обратной функции).Для дифференцируемой функции с производной, отличной от нуля, производная обратной функции равна обратной величине производной данной функции, т.е 2.Теорема Если функция x=φ(t) имеет производную в точке t0, а функция y=f(x) имеет производную в точкеx0=φ(t0), то сложная функция y(t)=f(φ(t)) имеет производную в точке t0 и справедлива формула: y/(t0)=f/(x0)·ϕ/(t0) .

Вопрос21. Логарифмическая производная. Производная функции .

Выбирается такая подстановка, в результате применения которой неопределенные интегралы от тригонометрических функций преоразющим в неопределённые интегралы от дробно рациональных функций вычисление интеграла вида SR(sinx,cosx)dx(1)

Теорема.

Неопределенный(1)подстановкой t=tgx/2(2)

Преобразует в неопределённость интеграл

Док-во:sinx=sinα x/2 cosx/2=

-числитель и знаменатель разделим на

Sinx=

Аналогично cosx=

X=2arctgt

dx=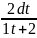

Интеграл(1) примет вид:SR(sinx,cosx)dx=SR( , )

-интеграл от рациональной дроби

Интегрируем и делаем обратную замену переменной

Замечание:В некоторых случаях применение универсальной подстановки(2)приводит к громоздким выкладкам.Если m и n – целые числа, то рассматривают следующие случаи при вычеслении интегралов вида.S xdx=S xdcosx

S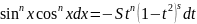

2=ns+1 Вторая подстановка- аналогично первой подстановке t=sinx

3) mtn=2s.Третья подстановка t=tgx.

S : -интеграл от рациональной функции

При вычеслении интегралов вида(1) при наличии равенства типа R(-sinx,cosx)=-R(sinx,cosx)целесообразна подстановка t=cos,если же подынтегральная функция нечетна относительна cosx, т.е

R(sinx,-cos)=-R’(sinx,cosx),то вычесление интеграла(1)значительно упрощается при использвании подстановки t=sin.В случае четности подынтегральной функции относительно sinx и cosx, т.е

R(-sinx,-cosx)=R(sinx,cosx)

Подстановка t tgx приводит к интегралу от рациональной функции

Для интегрирования функций sinx cosmx,cosnx cosmx,sinx sinmx могут быть использованы след. формулы:

Sina cosb=0,5/sin(a-b)+sin(a+b));

Cosa cob=0,5/cos(a-b)+cos(a+b));

Sina sinb=0,5/cos(a-b)-cos(a+b).

Производная функции u(x)^v(x): Найдем lny=ᵠ(x)lnf(x).Дифференцируя, получим y′/y=ᵠ′(x)lnf(x)+ᵠ(x)(lnf(x)′)=ᵠ′(x)lnf(x)+ᵠ(x)f′(x)/f(x). Учитывая, что y=f(x)^ᵠ(x), получим после преобразований y′=ᵠ(x)f(x)^ᵠ(x)-1 *f′(x)+f(x)^ᵠ(x) lnf(x)ᵠ′(x), т.е для того чтобы найти производную степенно-показательной функции, достаточно фиыыеринцировать ее вначале как степенную, а затем как показательную, и получкенные результаты сложить.

Вопрос22.Дифференцирование функций, заданных неявно и параметрически.

Неявно заданная функция

Если функция задана уравнением у=ƒ(х), разрешенным относительно у, то функция задана в явном виде (явная функция).

Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у.

Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот.

Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у+2х+cosy-1=0 или 2^у-х+у=0).

Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у'.

Производная неявной функции выражается через аргумент х и функцию у.

Функция, заданная параметрически

Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений где t — вспомогательная переменная, называемая параметром.

Найдем производную у'_х, считая, что функции (21.1) имеют производные и что функция х=x(t) имеет обратную t=φ(х). По правилу дифференцирования обратной функции Функцию у=ƒ(х), определяемую параметрическими уравнениями (21.1), можно рассматривать как сложную функцию у=y(t), где t=φ(х). По правилу дифференцирования сложной функции имеем: у'_х=y'_t•t'_x. С учетом равенства (21.2) получаем Полученная формула позволяет находить производную у'_х от функции заданной параметрически, не находя непосредственной зависимости у от х.