Ответы по математическому анализу 2012.

Вопрос 1. Предел последовательности. Геометрический смысл предела.

Пусть каждому по некоторому закону поставлено в соответствие действительное число xn. Тогда говорят, что определена последовательность чисел x1,x2,…,xn или {xn}. Число xn –элемент последовательности. Если xn=const, то последовательность называется постоянной. Последовательность {xn} ограничена, если . Число а называется пределом числовой последовательности {xn}, если для любого положительного числа ε существует номер N такой, что при всех n>N выполняется неравенство . Обозначение: или . Последовательность, имеющая предел называется сходящейся, не имеющая его – расходящейся. ГЕОМЕТР.СМЫСЛ: состоит в том, что все точки последо-ти, начиная с некоторого номера попадают в -окрестность точки А какой бы малой эта окрестноть не была. Вне окрестности остаются лишь конечное число точек.

Вопрос 2. Леммы о бесконечно малых величинах.

Переменная называется бесконечно малой, если её пределом является нуль.

ЛЕММА 1:Алгебраическая сумма конечного числа бесконечно малых, есть величина бесконечно малая. Доказательство: Рассмотрим, например, сумму 3-х бесконечно малых. 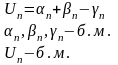Возьмем любое E > 0, т. к. ,то по определению существует номер n такой, что будет выполняться три неравенства: Существует номер n, такой, что при n > N выполняется неравенство: для , это и означает, что .

Лемма2:Произведение ограниченной переменной на бесконечно малую, есть велечина бесконечно малая. Док-во: Пусть(хn)- ограниченная переменная, т.е сущ., такое число М>0, что для всех n выполняется неравенство(xn)≤M. Пусть (Лямбn) есть БМ послед-ть. Тогда для любого E>0 сущ. Номер N, что при n>N выполняется неравенство (Лn)<E/M. Имеем( Лn*Xn)=(Лn)*(Xn)≤E/M*M=E.

Вопрос 3. Существование предела у ограниченной монотонной последовательности.

Если (Xn)-монотонно возрастающая и ограниченная сверху послед-ть, то она имееь конечный предел. Док-во: Итак, Xn не превосходит Xn+1 для всех, nа также существует такое число M, что для всех элементов Xn выполняеться неравенство Xn<=M. Данная послед-ть представляет обой числовое множество, ограниченное сверху и непустое. Тогда это множество имеет точную верхнюю грань ,обозначим это число через А и док-м, что она явл., пределом данной послед-ти. По св-ву верхней грани числового множества( Xn) для любого E >0. Существует N; XN≥a-E. Т.к. (Xn)-неубывающая послед-ть, то для всех n>N будет Xn> a-E. Но по определению верхней грани, для любого Xn≤ a+E.Следовательно, при n>N справедливы неравенства a-E<Xn, <a+E, т.е (Xn-a)<E окуда след., что число a- предел послед-ти.

Вопрос 4. Арифметические операции над сходящимися последовательностями.

Теорема: Предел суммы двух сходящихся послед-ей равен сумме их пределов, т.е lim( Xn+yn)=a±b. Док-во: Представим общие члены послед-ей в виде: Xn= a+λn; yn= b+βn, где dn=>0 и βn>0. Имеем: Xn±yn=(a±b)+(λn±βn). По лемме1 переменная(λn±βn), значит lim( Xn+yn)=a±b. Теорема: Предел произведении двух сходящихся послед-ей равен произведению их пределов, т.е lim( Xn+yn)=a*b. Теорема: Предел частного двух сходящихся послед-ей равен отношению их пределов. Если предел знаменателя отличен от нуля, т.е limXn/Yn=a/b, причем b≠0