
- •2. Способы изображения статистических данных
- •3. Виды, методы и способы формирования выборочной совокупности
- •5. Статистические показатели. Средние величины
- •2. Расчет месячной заработной платы рабочих по заводу за май осуществляется по формуле средней гармонической:
- •Задача 5
- •Задача 6
- •6. Показатели вариации
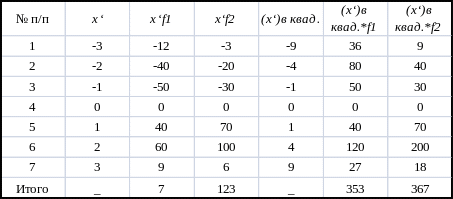
- •Задача 7
- •8. Индексный метод в исследовании социально-экономических процессов
- •Задача 11
- •Задача 12
- •9. Структура населения. Показатели статистики населения
- •Задача 14
- •Задача 15
- •Задача 16
- •Задача 17
- •Задача 18
Задача 6
Имеются данные о среднемесячной заработной плате рабочих фабрики.

Вычислить по каждому цеху среднюю заработную плату способом моментов.
Решение
Рассчитаем сокращенные значения вариант по формуле:
![]()
где A – 18000 руб., i – величина интервала, равная 100.
Для первого цеха.
1. Момент первого порядка — средняя арифметическая из новых значений вариант (х'):
![]()
2, Средняя арифметическая способом моментов:
![]() - средняя заработная плата рабочих
первого цеха.
- средняя заработная плата рабочих
первого цеха.
Рассчет по второму цеху аналогичен.
Задача решена.
Средняя геометрическая величина применяется в тех случаях, когда индивидуальные значения признака представляют собой относительные величины динамики, построенные в виде цепных величин как отношение каждого уровня в ряду динамики к предыдущему уровню.Она характеризует средний коэффициент роста.
Средняя геометрическая исчисляется извлечением корня степени п из произведений отдельных значений — вариантов признака х:
(7.4)![]()
где п — число вариантов; П — знак произведения; i = 1, 2, ..., п.
Наиболее широкое применение средняя геометрическая получила для определения средних темпов изменения в рядах динамики, а также в рядах распределения.
Структурные средние применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана.
Мода (Мо) — значение случайной величины, встречающееся с наибольшей вероятностью в дискретном вариационном ряду, т. е. вариант, имеющий наибольшую частоту.
Мода широко используется в статистической практике при изучении покупательского спроса, регистрации цен и т. п.
Медиана (Me) — это вариант, который находится в середине вариационного ряда. Медиана делит ряд на две равные (по числу единиц) части — со значениями признака меньше и больше медианы. Чтобы найти медиану, необходимо отыскать значение признака, которое находится в середине упорядоченного ряда.
Медиана находит практическое применение в маркетинговой деятельности.
Мода и медиана в отличие от степенных средних являются конкретными характеристиками, их значение имеет какой-либо конкретный вариант в вариационном ряду. Также они являются дополнительными к средней характеристиками совокупности и используются в математической статистике для анализа формы рядов распределения.
6. Показатели вариации
Средняя величина дает обобщающую характеристику признака изучаемой совокупности, но она не раскрывает строения совокупности, которое весьма существенно для ее познания. Средняя не показывает, как располагаются около нее варианты осредняемого признака, сосредоточены ли они вблизи средней или значительно отклоняются от нее. Вот почему ограничиваться вычислением одной средней в ряде случаев нельзя. Нужны и другие показатели, характеризующие отклонения отдельных значений от общей средней.
Возникает необходимость измерять вариацию признака в совокупностях. Для этой цели в статистике применяют ряд обобщающих показателей — показатели вариации. Вариация — это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени. Например, работники фирмы различаются по доходам, затратам времени на работу, росту, весу и т. д. К показателям вариации относятся: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации.
Самым элементарным показателем вариации признака является размах вариации (R), представляющий собой разность между максимальным и минимальным значениями признака в изучаемой совокупности:
(8.1)![]()
Однако размах вариации показывает лишь крайние отклонения признака и не отражает отклонений всех вариантов в ряду. Колебания варьирующего признака и их обобщенную характеристику дает среднее линейное отклонение.
Среднее линейное отклонение (![]() )
представляет собой среднюю арифметическую
абсолютных значений отклонений отдельных
вариантов от их средней арифметической
(при этом всегда предполагают, что
среднюю вычитают из варианта х-
)
представляет собой среднюю арифметическую
абсолютных значений отклонений отдельных
вариантов от их средней арифметической
(при этом всегда предполагают, что
среднюю вычитают из варианта х-![]() .).
.).
Среднее линейное отклонение рассчитывается по формуле:
для несгруппированных данных —
(8.2)![]() ,
,
где п — число членов ряда;
для сгруппированных данных —
(8.3)![]() ,
,
Где Σf сумма частот вариационного ряда.
Среднее линейное отклонение как меру вариации признака применяют в статистической практике редко (только в тех случаях, когда суммирование показателей без учета знаков имеет экономический смысл).
Дисперсия (σ2) Признака представляет собой средний квадрат отклонений вариантов от их средней величины и вычисляется по формулам простой и взвешенной дисперсий (в зависимости от исходных данных):
Простая дисперсия для несгруппированных данных:
(8.4)σ2 = ![]() ;
;
взвешенная дисперсия для вариационного ряда –
(8.5)![]() ;
;
Среднее квадратическое отклонение (σ) — это обобщающая характеристика размеров вариации признака в совокупности. Оно показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения.
Среднее квадратическое отклонение (σ) равно корню квадратному из дисперсии:
для несгруппированных данных —
(8.6)![]()
для вариационного ряда -
(8.7)![]() ;
;
В статистической практике часто возникает необходимость сравнения вариаций различных признаков. Для осуществления такого рода сравнений, а также сравнений колеблемости одного и того же признака в нескольких совокупностях с различным средним арифметическим используют относительный показатель вариации — коэффициент вариации.
Коэффициент вариации (v) представляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:
(8.8)![]() .
.
Коэффициент вариации используют не только для сравнительной оценки вариации единиц совокупности, но и для характеристики однородности совокупности. Совокупность считается количественно одно» родной, если коэффициент вариации не превышает 33 %.
Расчет показателей вариации способом моментов менее трудоемок, Дисперсия по способу моментов равна квадрату величины интервала, умноженному на разность момента второго порядка и квадрата момента первого порядка:
(8.9)![]()
где i — величина интервала; т1 — момент первого порядка; m2— момент второго порядка. Рассмотрим пример.
