1.4.2. Евклидовы пространства

В евклидовых пространствах вводится понятие скалярного произведения, а уже на

его основе определяется норма.

Пусть в действительном линейном пространстве L задан функционал .

Значение этого функционала называется скалярным произведением и обозначается x,y

если выполняются следующие условия:

1.

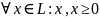
2.

3.

4.

5.

Линейное пространство с заданным в нем скалярным произведением называется

евклидовым пространством. Иногда евклидовы пространства называются предгиль-

бертовыми пространствами, а для скалярного произведения используется обозна-

чение .

Норма в евклидовом пространстве вводится формулой

Можно проверить, что все аксиомы нормы оказываются при этом выполненными.

В евклидовом пространстве может быть задан угол между векторами. Для ненуле-

вых векторов x L,y угол определяется выражением

cos =

Можно доказать, что, как и должно быть, правая часть равенства не превосходит

единицы.

Если для ненулевых векторов x L,y имеем x, y =0 , то , а векторы

x и y называются ортогональными.

Система ненулевых векторов из L называется ортогональной, если они попар-

но ортогональны:

Счетность множества не предполагается.

Упражнение 1.6

Доказать, что если векторы ортогональны, то они линейно независимы.

Если система векторов (семейство элементов) ортогональна и полна в L, то

она называется ортогональным базисом пространства L. Если при этом

, то имеем ортогональный нормированный базис или ортонормальный

базис. Если — ортогональная система, то — ортонормальная.

Примеры евклидовых пространств.

1. Пространство действительных чисел R. Скалярное произведение — обычное

произведение действительных чисел.

2. — n- мерное арифметическое пространство с элементами вида , где — действительные числа. Операции сложения и умножения на числа — общеизвестны, а скалярное произведение задается соотношением ,

3. Линейное пространство a, b непрерывных на a, b действительных функ-

ций со скалярным произведением

является евклидовым пространством. Можно установить, что все аксиомы ска-

лярного произведения оказываются выполненными.

В этом случае норма, очевидно, задается выражением

Индуцированная этой нормой метрика имеет вид

что совпадает с ранее введенной метрикой при наделении данного множества

функций структурой метрического пространства и выборе обозначения a, b .

Одним из ортогональных базисов пространства a, b является тригонометрическая система функций:

n=1,2,….,

4. Ранее рассматривалось также метрическое пространство a, b с метрикой

Норма определялась формулой

(Было установлено, что это банахово пространство.)

Поставим вопрос, можно ли наделить данное нормированное пространство

структурой евклидова пространства. Для этого достаточно задать вышеприве-

денную норму с помощью некоторого скалярного произведения:

Можно показать, что ответ будет отрицательным. Норму пространства C a, b нель-

зя задать с помощью скалярного произведения. Таким образом, не все нормирован-

ные пространства можно "превратить" в евклидовы пространства. Евклидовы про-

странства составляют лишь часть нормированных пространств. Еще раз отметим, что

пространство C a, b дает пример банахова, но не евклидова пространства.

Можно доказать следующее утверждение (характеристическое свойство евклидовых пространств).

Теорема 1.8 . Для того чтобы нормированное пространство L было евклидовым, необходимо и достаточно, чтобы для выполнялось равенство

Доказательство опускаем.

Теорема 1.9 (процесс ортогонализации Шмидта). Пусть

есть линейно независимая (счетная) система векторов в евклидовом пространстве

L. (Ясно, что в эту систему не могут входить нулевые векторы, иначе получим ли-

нейную зависимость). Тогда в L существует система векторов

Такая что

1. -ортонормальна

2.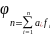 причем

(Переход от линейно независимой системы векторов к ортогональной называет-

ся процессом ортогонализации.)

Доказательство. Положим

В этом случае вектор будет ортогонален всем векторам , i=1, ..., . n Дейст-

вительно,

Для n=1 имеем

Но

,

Установлена ортогональность и 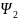. Покажем по индукции, что система векто-

ров , . ., , . ., построенная согласно выражению (1.3), ортогональна.

Пусть , . ., , . ., уже построены и ортогональны. Покажем, что тогда вектор ,

будет ортогонален всем , . ., 1, ..., n

Имеем (для любого фиксированного j =1, . ., n :

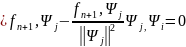
(Очевидно, в данном выражении только одно слагаемое суммы не равно нулю,

а именно слагаемое с индексом i= j . Остальные слагаемые равны нулю, т. к. ,

i=1, ..., n ортогональны и =0, i j .)

Последнее соотношение может выполняться и если в результате процедуры (1.3)

будут все время получаться нулевые векторы. Покажем, что это невозможно из-за

линейной независимости системы векторов Действительно, пусть

получили, 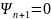тогда

что противоречит линейной независимости . Следовательно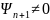 . Для окончательного доказательства теоремы достаточно положить

Теорема доказана.