1.3.2. Выпуклые множества

Пусть L — линейное действительное пространство и . Замкнутым

отрезком (или сегментом) в L, соединяющим точки и , называется совокупность элементов вида

В случае 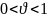имеем открытый отрезок.

Множество A L называется выпуклым, если выполняется следующее соотношение

Таким образом, выпуклое множество вместе с любыми своими двумя точками

должно содержать и отрезок, соединяющий эти точки. Очевидно, само пространст-

во L — выпукло.

Ядром J E произвольного подмножества E L называется множество, удовле-

творяющее следующим условиям: x J E тогда и только тогда, когда для y L

существует число 0 такое, что для всех t,

Здесь y задает направление, а число t — продвижение по этому направлению. Оче-

видно, элементы ядра принадлежат E, но не все элементы E входят в ядро.

Множество E L называется телом, если J E

. Если выпуклое множество

E — тело, то оно называется выпуклым телом.

Примеры.

1. В пространстве куб и шар являются примерами выпуклых тел. Отрезок,

плоскость, треугольник в том же пространстве — выпуклые множества, но не

выпуклые тела.

2. Рассмотрим множество C непрерывных на отрезке a, b функций и его под-

множество, удовлетворяющее условию . (Сами функции из

G вовсе не обязаны быть выпуклыми в обычном смысле.) Можно доказать, что

G — выпуклое тело.

Докажем утверждение из примера 2. Множество G — выпукло. Действительно, ес-

ли g, f G , то . При 0 имеем

Таким образом, отрезок, соединяющий точки g, f, также входит в множество G и,

следовательно, G — выпукло. Проверим, является ли это множество выпуклым

телом. Для этого необходимо и достаточно доказать, что J G

. Рассмотрим во множестве G функцию тождественно равную нулю. Покажем, что

и, следовательно, J G

. Действительно, рассмотрим и выражение

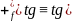. Ясно, что 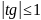при . Таким образом, G — выпуклое тело.

Теорема 1.5. Пересечение любого числа выпуклых множеств есть выпуклое мно-

жество.

Доказательство ясно.

Пересечение выпуклых тел, будучи выпуклым множеством, также будет выпуклым

множеством, но выпуклым телом может и не быть. Например, если рассечь куб в

трехмерном пространстве плоскостью, то обе части куба будут выпуклыми телами,

а само сечение — нет.

1.4. Нормированные пространства

В теории метрических пространств сформулировано понятие расстояния между

элементами произвольного множества. В этом смысле метрические пространства

являются частным случаем более общих топологических пространств. Концепция

же линейных пространств позволяет наделить множество некоторой алгебраиче-

ской структурой с помощью определения операций сложения элементов и умноже-

ния их на числа. Нормированные пространства являются одновременно линейными

и метрическими пространствами и относятся к важному классу топологических ли-

нейных пространств. Развитие теории нормированных пространств связано с име-

нем Стефана Банаха и целого ряда других авторов. Структура нормированных про-

странств оказывается чрезвычайно удобной для изучения основных конструкций

теории оптимизации в достаточно общем виде.