Билет 1.

1.Состояние как фундаментальная характеристика термодинамических систем. Виды тернмодинамических состояний.

Состояние это фундаментальная характеристика, определяет запас энергии внутренней и направления ее переноса.

Состояние в термодинамике

1 Равновесное (внутренная энергия имеет миним значение, все процессы обратимы, равновесные процессы изображены в диаграмме состояния (она же диаграмма равновесия, фазовая диаграмма плавкости)

2 Неравновесное (избыток внутр энергии до максим, может самопроизвольно перейти в равновесное состояние)

3 Метастабильное (с промежуточным запасом внутр энергии, самостоятельно перейти в стабильное состояние не может)

4 Стационарное (в системе развиваются процессы независящие от времени, поцесс кристаллизации)

Параметры термодинамической системы.Состояния систем характеризуются параметрами состояния и функциями состояния.Параметры состояния системы – это свойства, однозначно характеризующие однородные части системы. Например, для идеального газа параметрами являются четыре свойства – давление P, объём V, температура T и количества молей µ . Любые три из них – независимы. Это означает, что, задав произвольно любые три из четырех параметров, мы по уравнению состояния (в данном случае это будет уравнение Клапейрона- Менделеева) найдем четвертый:PV= µ RT. Для более сложных систем могут появиться дополнительные параметры состояния – например, химический состав. Параметры делятся на интенсивные и экстенсивные. Интенсивные параметры не зависят от количества вещества в системе (давление,температура, напряженность электрического поля и др.), а экстенсивные –зависят (объем, масса, заряд и др.)Функци состояния термодинамической системы:Параметры состояния связаны друг с другом функциональными зависимостями. Те из функций, которые не зависят от истории системы,т.е. от того, как она попала в данное состояние, называются функциями состояния. Они однозначно характеризующие это состояние. По аналогии с первым и вторым началами термодинамики, каждое из которых ( как это будет показано в последующем) устанавливает существование определенной величины - функции равновесного состояния термодинамической системы.

Второй закон термодинамики представляет собой ряд положений, относящихся к различным состояниям и процессам в термодинамической системе. Равновесным состоянием термодинамической системы называют состояние, при котором параметры состояния неизменны при неизменных внешних условиях.

В термодинамике внутренняя энергия определяется следующим образом. Примем произвольное равновесное состояние термодинамической системы за нулевое, то есть будем считать, что внутренняя энергия системы в этом состоянии равна нулю. Внутренней энергией системы в каком-либо равновесном состоянии называется работа внешних сил по переводу системы любым адиабатическим путем из нулевого состояния в рассматриваемое состояние. Если такой перевод невозможен, внутренней энергией называется взятая с противоположным знаком работа внешних сил по переводу системы любым адиабатическим путем из рассматриваемого состояния в нулевое.

Отыскание равновесного состояния изолированной системы методами классической термодинамики сводится к отысканию состояния, для которого ( fS) E равно нулю. Этот метод отыскания равновесного состояния термодинамической системы аналогичен методу возможных перемещений в теоретической механике.

Мы знаем, что равновесное состояние термодинамической системы полностью описывается заданием ее внутренней энергии, объема и числа частиц. И, поскольку объем и число частиц разных тел, находящихся в тепловом контакте, могут оставаться неизменными при выравнивании их температуры, мы должны заключить, что изменение последней происходит в этом случае только вследствие перераспределения между ними энергии.

Положение о существовании температуры может быть сформулировано также следующим образом. мы установили, что равновесное состояние термодинамической системы характеризуется внешними и внутренними параметрами, причем внутренние параметры зависят от положения и движения молекул системы и значений внешних параметров.

Положение о существовании температуры может быть сформулировано также следующим образом. мы установили, что равновесное состояние термодинамической системы характеризуется внешними и внутренними параметрами, причем внутренние параметры зависят от положения и движения молекул системы и значений внешних параметров. Положение же о существовании температуры устанавливает, что состояние термодинамического равновесия определяется совокупностью внешних параметров и температурой. Термодинамика изучает законы взаимных превращений различных видов энергии, состояния равновесия и их зависимость от различных факторов, атакже возможность, направление и предел протекания самопроизвольных процессов. Термодинамика использует свой особый так называемыйфеноменологический метод подхода к решению тех или иных вопросов. Сущность этого метода состоит в обобщении опытных данных в виде трех законов — начал термодинамики — с их дальнейшим применением к различным вопросам и конкретным условиям без учета детального строения рассматриваемых систем.Особенностью термодинамического метода является его применимость только к системам, состоящим из очень большого числа отдельных частиц, а также определение лишь возможности рассматриваемых процессов. Вопрос о скоростипроцесса термодинамическим методом также не может быть рассмотрен.     Подразделяя признаки системы на параметры и функции состояния, мы только утверждаем, что в состоянии равновесия определенным значениям параметров соответствуют определенные значения каждой функциисостояния. Однако в громадном числе случаев или неизвестен вид этих функций или наши знания недо-достаточно полны, и мы не в состоянии, пользуясь одними только термодинамическими соотношениями, установить численные значенияизменений различных признаков по приращениям параметров. Чтобы пояснить эту мысль, приведем три примера.     Если же продукт реакции получается с хорошим выходом, то это означает, что или равновесие сдвинуто в сторону образования данного продукта, или он образуется с заметной скоростью при необратимом процессе. В первом случаедействует фактор равновесия, или термодинамический контроль(термодинамика имеет дело с физическими или химическими системами всостоянии равновесия), во втором — фактор скорости, или кинетический контроль. Важно знать, какой вид контроля действует в каждой конкретной реакции, так как увеличение выхода продукта реакции в обоих случаях достигается совершенно различными способами.

2. Характеристики прочности материалов при статическом растяжении.Истинные и условные напряжения течения. Критерий статической прочности.

Статическое растяжение — одно из наиболее распространённых видов испытаний для определения механических свойств материалов.

Виды и характеристика прочности

Одной из наиболее важных характеристик конструкционных материалов являются механические свойства, которые определяются их способностью сопротивляться действию внешних сил или нагрузок. К таким свойствам прежде всего относятся прочность и пластичность.

Прочностью называется свойство твердых тел (материалов) сопротивляться разрушению или деформации под действием внешних нагрузок.

Пластичностью называется свойство твердых тел (материалов) изменять под действием внешних сил без разрушения свою форму и размер и устойчиво сохранять эти изменения после снятия нагрузок.

Прочность и пластичность являются комплексными характеристиками твердых тел и зависят как от внутренних (присущих собственно материалу), так и внешних (обусловленных условиями эксплуатации) факторов. К внешним факторам относятся - температура, время и скорость нагружения, характер приложения нагрузки (постоянная, знакопеременная), схема напряженного состояния. К внутренним факторам относятся – химический и фазовый состав материалов, их кристаллическая и зеренная (форма и размер зерен) структура, состояние (литое, деформированное, закаленное, отожженное, состаренное, отпущенное), дефектность и др. Прочность и пластичность материалов напрямую зависят от сил внутренних межатомных связей и от препятствий пластическому деформированию.

Различают несколько видов прочности:

- статическую (кратковременную),

- конструкционную,

- динамическую (ударную),

- длительную (жаропрочность),

- усталостную - циклическую и контактную,

- удельную,

- механическую.

Определяющими видами прочности являются: статическая с критерием – временное сопротивление, конструкционная – критерии – прочность, надежность и долговечность, жаропрочность – пределы ползучести и длительной прочности, усталостная – выносливость.

Статическая (кратковременная) прочность – это прочность, которой обладает материал при статическом (быстром или медленном) нагружении в режиме растяжения, сжатия, кручения, изгиба. Разрушение материала происходит вследствие разрыва – хрупкое разрушение или сдвига – вязкое разрушение. На практике разрушение происходит при совместном действии отрыва и сдвига. Чаще всего статическая прочность определяется при испытаниях на одноосное растяжение, поскольку одноосное растяжение сравнительно легко поддается анализу, позволяет по результатам одного опыта определять сразу несколько важных механических характеристик материалов, являющихся критерием его качества и лежащих в основе инженерных расчетов. Статической прочности соответствует закаленное состояние сплавов, со структурой мартенсита или пересыщенного твердого раствора.

Характеристики прочности

 

1. Предел пропорциональности Опц =  Fпц / Ao - наибольшее напряжение растяжения, при котором еще справедлив закон Гука. Здесь Fпц - нагрузка, определяемая по отклонению диаграммы (рис. 6, а) от первоначального прямолинейного участка.

 

2. Предел упругости  Oу = Fy / Ao - представляет собой напряжение,

при котором остаточные деформации незначительны (0,001 - 0,003 %).

Практически можно считать предел упругости совпадающим с пределом пропорциональности.

 

3. Предел текучести От = Fт / Ao - напряжение, при котором наблюдается рост деформаций при постоянной нагрузке.

 

4. Предел прочности или временное сопротивление материалов Oв = Fmax / Ao - напряжение, вызванное наибольшей нагрузкой.

 

5. Истинное сопротивление разрыву  Sk = Fk / Ak - напряжение, определяемое отношением нагрузки Fк в момент разрыва к площади поперечного сечения образца в месте разрыва.

  Напряжения Oпц, От, Oпч являются уловными, т.к. они определяются по отношению к первоначальной площади поперечного сечения образца без учета уменьшения этой площади в процессе роста нагрузки.

7 Механические напряжения бывают истинными и условными в зависимости от изменения площади поперечного сечения. Если изменения незначительны, т.е. F₀ = F_K , то такие напряжения называются условными – σ, τ . Если первоначальное сечение со временем меняется существенно, то соответствующие напряжения называются истинными. Нормальные обозначаются буквой S, а касательные - t. Поскольку F_K < F₀, то всегда при растяжении истинные напряжения будут больше условных. Физический смысл имеют только истинные напряжения, однако на практике для описания реальных конструкций и сооружений, когда ΔF ≈ 0, удобно пользоваться условными напряжениями.

На основании вышеизложенного, можно дать следующие определения напряжения:

- Усилие, действующее на единицу площади, называется напряжением.

- Напряжением называется приложенная к телу нагрузка, отнесенная к единице площади его сечения.

Кратковременная или статическая прочность определяется в экспериментах на растяжение при комнатной температуре на испытательных машинах механического или гидравлического типа до разрушения (ГОСТ 1497-73). Полученные результаты фиксируются графически в виде зависимости между приложенным усилием и уд­линением образца (рисунок 4.1). Первичная кривая испытаний называется диаграммой деформации.

Если нагрузку относить к действительному сече­нию, то получают значения истинных напря­жений. Диаграммы истинных напряжений дают представление о физических процессах, протекающих в материале, и имеют особое зна­чение для прочностных расчетов и технологии обработки металлов давлением.

Деформация образца при нагружении сплава сначала является макроупругой, а затем постепенно и в разных зернах при неодина­ковой нагрузке переходит в пластическую, про­исходящую путем сдвигов по дислокационному механизму. Накопление дислокаций в результате деформации ведет к упрочнению металла, но при значительной их плот­ности, особенно в отдельных участках, возникают очаги разрушения, приводящие в конечном счете к полному разрушению образца в целом. Схематически процесс деформации от упругой до пластической представлен на рисунке 4.2.

При испытаниях на растяжение определяют следующие характеристики:

- предел пропорциональности (условный) σ_пц - напряжение, при котором от­ступление от линейной зависимости между осевой растягивающей нагрузкой Р и удлинением (Δl = l_к – l₀) достигает такой величины, что тангенс угла наклона, образованного касательной к кривой деформации Р – Δ1 в точке Р_пц с осью нагру­зок, увеличивается на 50 % от своего значения на линейном упругом участке; соответствует точке р

- предел упругости (условный) σ_0,05 – напряжение, при котором остаточное уд­линение достигает 0,05 % от длины участка образца, равного базе тензометра, МПа;

- предел текучести (физический) σ_т – наименьшее напряжение, при котором об­разец деформируется без заметного увеличения растягивающей нагрузки, МПа;

- предел текучести (условный) σ_0,2 – напряжение, при котором остаточное удли­нение достигает 0,2 %, МПа;

- временное сопротивление σ_в – напряжение, соответствующее наибольшей на­грузке Р_max, предшествующей разрушению образца, МПа;

- S_к – истинное сопротивление разрыву (разрушению),

- σ – напряжение, определяемое отношением нагрузки Р_max в момент разрыва к площади поперечного сечения образца в месте разрыва F_к, МПа;

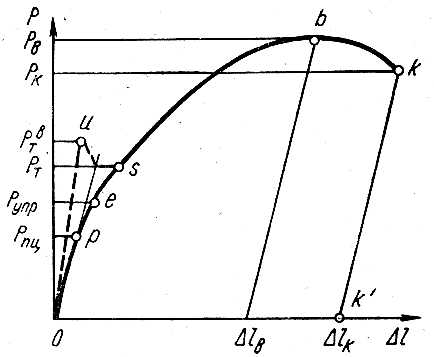
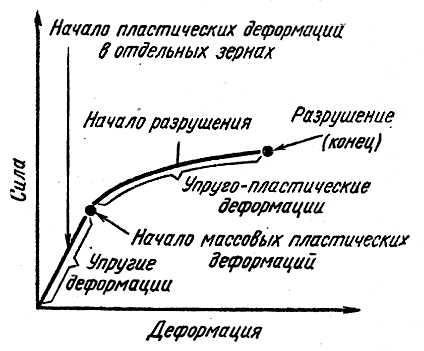
Рисунок – 4.1 Характерные точки на диаграмме растяжения для расчета прочностных характеристик	Рисунок – 4.2 Схема процесса деформации

За меру статической прочности принимается временное сопротивление σ_в=Р_макс./F_o, по достижении которого пластическая деформация переходит от равномерной к сосредоточенной (локальной) на определенном участке образца, что проявляется в образовании шейки. Можно сказать, что при данном значении напряжения образец (материал) теряет прочность как целостный объект испытаний, поскольку начинается его разрушение.

Билет 2

1.Жаропрочность и критерии ее оценки. Температурные интервалы проявления жаропрочных свойств и их характеристика

Жаропрочность - весьма сложное свойство и характеризует способность материалов сопротивляться деформации и разрушению при повышенных температурах в течение длительного времени. Определяющими, как и в прочности вообще, являются процессы деформации (ползучести) и разрушения. Однако в поведении металлов под нагрузкой при высоких температурах (Т ≥ 0,4 Т_пл) имеется специфика, связанная с возрастанием роли температурного фактора. Особое значение приобретает стабильность заданной структуры. При высоких температурах возрастает интенсивность диффузионных процессов, что способствует изменению структуры и свойств. В условиях высокотемпературной деформации. в ди­слокационных моделях, описывающих ползучесть и разрушение металлов и сплавов, необходимо учитывать и диффузионные процессы.

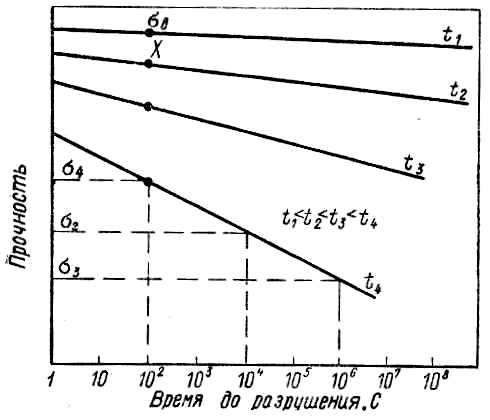
Рисунок – 7.1 Зависимость прочности от продолжительности испытания

Отличительной особенностью жаропрочности является ее зависимость от продолжительности приложения нагрузки (рисунок 7.1). Напряжение, которое вызывает разрушение материала может быть высоким при кратковременном нагружении и резко снижаться при длительном воздействии нагрузки. Вместе с тем, чем выше нагрузка. тем ниже разрушающее напряжение при заданном времени ее действия. Следовательно, в общем случае при повышенных температурах прочность материала определяется двумя факторами – температурой и временем. Как следует из рисунка 7.1, прочность металлов и сплавов при пониженной температуре мало зависит от продолжительности нагружения, и время до разрушения обычно исчисляется годами (прямые t₁, t₂). При более высоких температурах зависимость прочности от времени становится сильнее (угол наклона соответствующих прямых возрастает – t₃, t₄).

Пределом длительной прочности называют напряжение, которое приводит к разрушению образца при заданной температуре за определенное время, соответствующее условиям эксплуатации изделий. Предел длительной прочности обозначают  , где индексы t и   указывают температуру (^оС) и время испытаний (ч).

Пределом ползучести называют напряжение, вызывающее заданную суммарную деформацию за определенное время при заданной температуре. Предел ползучести обозначают  , где t – температура, ^оС;   – суммарное удлинение, %;   – время, ч. Для деталей, длительное время работающих при повышенных температурах, задается обычно скорость ползучести на установившейся стадии процесса, например 0,1 % за 10⁴ ч или за 10⁵ ч.

2 Деформационное упрочнение металлов и сплавов. Стадии и механизм реализации деформационного упрочнения

Деформационное упрочнение существенно влияет на величину физических свойств. Так, объемная пластическая деформации приводит к увеличению твердости, удельного электросопротивления ( максимально до 6 %), коэрцитивной силы; возрастает склонность к коррозии, и, наоборот, снижаются плотность, магнитная проницаемость и величина остаточной индукции ферромагнитных материалов; поверхностная - повышает твердость, сопротивление коррозии.Деформационное упрочнение обычно не возникает при горячем деформировании. Деформационное упрочнение при пластической деформации возникает из-за затруднения движения дислокаций, когда исчерпываются возможности скольжения (двойникования) в данных плоскостях. При этом происходит повышение плотности и увеличение кривизны дислокаций, образуются точечные дефекты и барьеры типа Ломера — Коттрелла, фрагменты и пересечения плоскостей скольжения, ступеньки на дислокациях, узлы и другие сложные дислокационные построения.[17, С.8]  Некоторые теории объясняют деформационное упрочнение полями близкодействующих напряжений [238, 239]. Например, Базинский [238] связывает упрочнение с упругим взаимодействием дислокаций, движущихся в данной плоскости скольжения, и лесом дислокаций, пересекающих эту плоскость (рис. 3.1, в). При этом напряжение течения[5, С.99]  В соответствии с этой моделью деформационное упрочнение на начальной стадии деформации (вплоть до 5 %) может быть объяснено увеличениемдислокационной плотности от 5 хЮ14 до 1015 м~2. Увеличение внутренних напряжений влияет на процесс образования дислокаций, препятствуя их выгибанию, и, таким образом, увеличивая величину приложенных напряжений, необходимых для продолжения деформации. В то же время увеличение внутреннего гидростатического давления при растяжении активизирует зернограничную диффузию и, как следствие, способствует протеканию процессов возврата. Схематическое изображение двух областей металлического кристалла, деформируемого силами сдвига (два слоя, непосредственно примыкающих к плоскости скольжения) [144] измерений [137] было показано, что каждой стадии деформационного упрочнения соответствует определенный тип субструктур, возникающих в начале стадии в недрах старой субструктуры и охватывающих к ее концу практически весь объем кристалла.

Бифуркационные диаграммы для фазовых переходов II (а) и 1(6) родов [147] упрочнения.

Последние относятся к сплавам со сверхструктурой L/2 (Ni3Ge, Ni3Ga, Ni3Al) и характеризуются аномальным поведением механических свойств или термическим упрочнением [153].

ГЦК-твердых растворов на основе никеля и меди появление элементов полосовой структуры соответствует переходу от стадии II деформационного упрочнения к стадии III.

Для ГЦК-кристаллов, продеформированных до начала II стадии упрочнения, указанное отношение составляет величину 0,07 ± 0,01, не зависящую от кристаллографической ориентации оси растяжения [171].

Так как основной вклад в запасенную энергию Ws вносят дислокации первичной системы скольжения, указанный экспериментальный результат согласуется с теоретической оценкой, вытекающей из классической теории деформационного упрочнения.

Как отмечалось ранее, в пластически деформируемых кристаллах в широком интервале температур и деформаций с удалением от термодинамического равновесия наблюдается образование субструктур дефектов, например, ячеистой дислокационной структуры на II—Ш стадиях упрочнения.

Для объяснения эффекта деформационного упрочнения исследуется устойчивость популяции s-дислокаций, которые рассматриваются как составляющие нелинейного нелокального континуума, находящегося вдали от термодинамического равновесия.

Периодические решения системы уравнений (115), (116), соответствующие образованию клубковой XK и ячеистой Хя субструктур [190] (а), и схема образования ячеистой дислокационной субструктуры [191] (б) плотностью s-дислокации: , е) = т0 + )F(r\) p(x + r\, где т0 — предел текучести материала, а интегральный член отвечает за нелокальность деформационного упрочнения на масштабах порядка 1 мкм.

При однородном распределении s-дислокаций уравнение (115) описывает обычное линейное упрочнение т = Т0 + Я0р, Я0 = }F(r\)dr\.

В результате анализа системы уравнений (115), (116) было показано, что для идеализированного случая, исключающего из рассмотрения эффект локализации пластической деформации, процесс деформационного упрочнения включает три основные стадии:

3) стадия стабилизации процессов производства и аннигиляции s-дисло-каций, соответствующая на кривой деформационного упрочнения стадии установившегося течения.

Указанные выше синергетические модели не только позволяют формально описать процесс образования дислокационных структур, но и способствуют более глубокому пониманию физической природы деформационного упрочнения [190].

Переход от ранней стадии деформационного упрочнения к установившейся стационарной стадии, на которой практически отсутствует эффект упорядочения, можно объяснить стремлением системы (деформируемого твердого тела) к минимуму своей внутренней энергии.

Действительно, на всех стадиях деформационного упрочнения общее количество произведенных в процессе деформации дислокаций существенно превышает то их количество, которое необходимо для поддержания самой пластической деформации.

В работах [192, 193] при теоретическом анализе кривых деформационного упрочнения получено уравнение эволюции суммарной плотности дислокаций с деформацией dp/dy-Ko + Kyp1/2-^.

Подробный анализ уравнения (118) позволил описать характерные стадии деформационного упрочнения ГЦК-монокристаллов, а также получить параболический закон упрочнения поликристаллов [192].

Деформационное упрочнение металлов обусловливается сложными коллективными процессами, включающими формирование диссипативных структур в виде пространственно-неоднородных стационарных состояний.

7,1 Механизмы разрушения жаропрочных материалов. Способы образования клиновидных трещин.

В зависимости от условий работы деталей при ползучести в жаропрочных материалах различают три вида разрушений:

– вязкое разрушение;

– образование и рост клиновидных трещин;

– разрушение порообразованием.

Вязкое разрушение часто имеет место при повышении температуры при работе труб поверхностей нагрева в условиях ползучести. Разрушение путем образования клиновидных трещин вызвано повышенным уровнем неучтенных расчетом напряжений в условиях стесненной деформации в зонах концентрации напряжений, а также может быть связано с охрупченным состоянием металла. Разрушение порообразованием обычно происходит в результате длительной эксплуатации.

Вязкое разрушение при ползучести по структурным признакам аналогично вязкому разрушению пластичных материалов при непрерывно возрастающих нагрузках (кратковременные испытания). Так же как и при непрерывно возрастающей нагрузке, вязкому разрушению при ползучести всегда предшествует большая макроскопическая пластическая деформация с образованием шейки .

При больших степенях деформации зерна структурных составляющих вытягиваются в направлении действующих напряжений. Внутри зерен формируется направленная субструктура. Несплошности типа полостей образуются на границах зерен и субграницах в направлении деформации. Разрушение происходит путем поперечного слияния несплошностей и носит внутризеренный характер.

Вязкое разрушение при ползучести происходит при высоких уровнях нагрузок. Снижение нагрузок приводит к развитию межзеренного разрушения. В зависимости от уровня температур и напряжений разрушение происходит преимущественно по одному из двух типов - образование клиновидных трещин или образование пор.

Клиновидные трещины образуются преимущественно в стыках трех зерен, развиваются вдоль одной из границ и связаны с заторможенным межзеренным проскальзыванием. Поперечные границы являются препятствием для распространения трещин, поэтому на начальной стадии процесса разрушения трещины распространяются от одного узла границы до другого.

Билет 3,4 (Фарида)

Билет 5 Билет № 5

1. Упрочнение материалов при твердорастворном механизме и механизме упрочнения избыточными фазами.

Твердорастворное упрочнение

При легировании металлов растворимыми добавками наблюдается повышение всех прочностных характеристик. В частности, предел текучести поликристаллических сплавав - твердых растворов замещения прямо пропорционален концентрации легирующего элемента до 10-30% (ат.). На рисунке 11.1 показаны, в качестве приме­ра, зависимости условного предела текучести σ_т твердых растворов на основе меди от содержания добавки. Видно, что разные легирующие элементы оказывают различное упрочняющее воздействие. Для твердых растворов замещения характерна линейная зависимость прочности от концентрации легирующего элемента, а для твердых рас­творов внедрения на основе о. ц. к. металлов чаще ха­рактерна пропорциональность предела текучести корню квадратному из кон­центрации. Важно подчерк­нуть, что, зная концентра­ционные зависимости пре­дела текучести двойных сплавов, можно с достаточно высокой точностью (при отсутствии упорядочения) рассчитывать предел текучести малолегиро­ванных многокомпонент­ных твердых растворов, ис­пользуя правило аддитивно­сти. Если, например, известно, что добавление 1 % (ат.) AI к меди вызывает прирост σ _0,2 на 60 МПа, то таким же будет эффект при легировании α-латуни, т.е. мо­жно без эксперимента определить σ _0,2 тройного твердого раствора Сu-Zn-Аl.

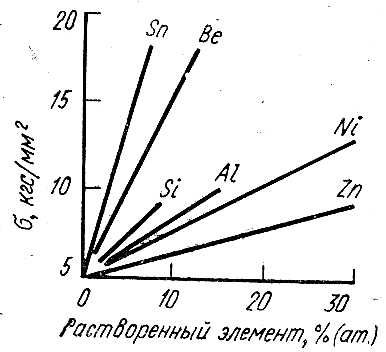
Рисунок – 11.1 Влияние концентрации легирующих элементов на прочность твердых растворов меди

Наиболее важными для теории легирования являют­ся вопросы механизма упрочнения и целенаправленного выбора легирующих элементов, дающих наибольший прирост прочностных свойств.

Повышенная прочность сплавов - твердых растворов по сравнению с чистыми металлами обусловлена:

1) увеличением сил трения при движении дислокаций;

2) образованием примесных атмосфер;

3) изменением дислокационной структуры при легировании.

Главной причиной увеличения сил трения является упругое взаимодействие скользящих дислокаций с ра­створенными атомами. Последние можно разделить на две большие группы: вызывающие вокруг себя искажения кристаллической решетки с шаровой симметрией (например, атомы элементов замещения) и вызывающие тетрагональные искажения решетки (например, атомы внедрения в металлах с о. ц. к. решеткой). Растворенные атомы, вызывающие тетрагональные искажения, приводят к возникновению больших упругих напряжений. В результате прирост сил трения и соответственно напряжений течения оказывается значительно больше, чем при введении атомов, вызывающих искажение ре­шетки с шаровой симметрией.

Величина упругих искажений решетки определяется также разницей в атомных размерах растворителя и до­бавки. Чем больше эта разница, тем сильнее прирост со­противления движению дислокаций в твердых растворах любого типа.

Даже при малых концентрациях второго компонента расстояния между его атомами настолько малы, что «проталкивания» дислокаций между ними не происхо­дит. Увеличение сопротивления движению дислокаций в решетке твердого раствора определяется статистической суммой положительных и отрицательных напряжений вокруг растворенных атомов. Количество этих атомов, приходящихся на длину дислокации L, пропорциональ­но L, а статистическая сумма напряжений пропорциональна L^1/2.

Известно, что сила, действующая на длину L дисло­кации

F = tbL (11.1)

Следовательно,

tbL = KL^1/2 (11.2)

откуда

t = K/bL^1/2 , (11.3)

где К – коэффициент.

Для расчета напряжения t необходимо оценить усредненную длину движущихся дислокационных петель L. Это весьма сложно сделать расчетным путем. По Моту и Набарро

t = Gθ²C (11.4)

Уточненные расчеты дают выражение

t = 2,5Gθ^4/3 C (11.5)

где θ – мера величины поля внутренних напряжений, определяемая разницей в размерах атомов основы и добавки;

С – атомная концентрация растворенного элемента.

Размерный фактор

, (11.6)

где a - межатомное расстояние.

Сопоставление расчетных значений t с эксперимен­тальными величинами критического напряжения сдвига монокристаллов показало, что предсказываемое упроч­нение примерно на порядок больше реального. Причиной такого расхождения может быть действие других механизмов твердорастворного упрочнения, которые не учитываются теорией Мотта и Набарро.

В частности, помимо упругого взаимодействия дви­жущихся дислокаций с растворенными атомами, увели­чение сил трения при легировании может вызываться различием упругих характеристик основы и добавки, упорядочением, влиянием легирования на силу Пайерл­са. Увеличение сил трения при образовании твердых рас­творов должна вызывать прирост всех характеристик сопротивления пластической деформации, начиная от предела упругости и кончая истинным сопротивлением разрыву.

Второй основной механизм твердорастворного уп­рочнения - образование примесных атмосфер на дис­локациях - действует в большинстве случаев лишь на начальных стадиях пластической деформации и влияет в основном на пределы упругости и текучести. Однако если при растяжении в образце идет динамическое де­формационное старение, то механизм закрепления дис­локаций примесными атмосферами может «работать» вплоть да поздних стадий деформации, обуславливая, в частности, прирост предела прочности.

Большое влияние оказывают примеси внед­рения, образующие атмосферы Коттрелла, на предел текучести о. ц. к. металлов. В твердых растворах с г. ц. к. и г. к. решетками важное значение имеет закреп­ление растянутых дислокаций атмосферами Сузуки, возникающими из-за разницы в растворимости легирующего элемента в дефекте упаковки и окружающей его матрице. Если коттрелловские атмосферы «размываются» при относительно низких температурах (часто <0,3-0,4 Т_пл.), то атмосферы Сузуки сохраняются вплоть до 0,5 - 0,55 Т_пл. Они соответственно обеспечивают прирост прочностных характеристик в более широком интервале тем­ператур испытания.

Притяжение растворенных атомов к дислокациям можно объяснить также их электростатическим взаимо­действием: ядра дислокации имеет электрический заряд и взаимодействует с дополнительным зарядом, который возникает у инородного атома с отличной от растворите­ля валентностью. Чем больше разница в валентностях, тем сильнее электростатическое взаимодействие. По рас­четным оценкам оно составляет около 20% упругого взаимодействия.

Третий механизм твердорастворного упрочнения свя­зан с влиянием легирования на дислокационную струк­туру. Мы уже знаем, что легирование может существенно сказываться на энергии дефекта упаковки в твердых растворах (обычно снижать ее). Наблюдающееся в ре­зультате этого затруднение поперечного скольжения вносит определенный вклад в прирост характеристик прочности, особенно на поздних стадиях деформации. Легирование, вызывая, блокировку дислокаций, уве­личение сил трения, изменение энергии дефекта упаков­ки, естественно приводит к формированию иных дислока­ционных структур во время растяжения. В результате на­блюдается определенное изменение механических свойств, связанное с влиянием собственно субструкту­ры.

Итак, легирование металлов растворимыми добав­ками вызывает упрочнение по целому ряду причин. Ме­ханизмы упрочнения весьма разнообразны и часто действуют совместно. В большинстве случаев мы еще не можем количественно оценивать вклад того или иного механизма в общее упрочнение. Однако даже качественный анализ этих механизмов позволяет наметить прин­ципиальные критерии выбора легирующих элементов для получения максимального твердорастворного уп­рочнения. К таким критериям можно отнести:

1) величину растворимости легирующего элемента в основе (прочностные свойства растут с увеличением легированности);

2) способ растворения атомов добавки (замещение или внедрение); .

3) разницу в атомных размерах добавки и основы;

4) разницу в валентностях легирующего элемента и растворителя;

5) разницу в упругих константах основы и добавки (чем больше эта разница, тем значительнее прирост прочностных характеристик).

При создании высокопрочных сплавов легирующие элементы стремятся выбрать таким образом, чтобы в максимальной степени использовать все перечисленные критерии. Однако сделать это на практике затрудни­тельно. Например, создание сильнолегированных твер­дых растворов внедрения невозможно из-за низкой раст­воримости элементов внедрения в металлах и высокой хрупкости растворов внедрения. Следует отметить, что вообще сильное твердорастворное упрочнение часто соп­ровождается снижением характеристик пластичности, по­скольку существенное ограничение подвижности дисло­каций должно вызывать уменьшение производимой ими деформации. Это не значит, однако, что любому твердора­створному упрочнению должно соответствовать снижение пластичности. Достаточно, часто, например, при увели­чении концентрации цинка в α-латунях, наблюдается па­раллельное .повышение прочности и пластичности твердых растворов.

Повышенная прочность твердых растворов по срав­нению с металлом - основой сохраняется лишь до тем­ператур испытания не выше 0,5-0,55 Т_пл. При более высоких температурах разница в их прочностных харак­теристиках нивелируется, так как блокировка и тормо­жение движущихся дислокаций растворенными атома­ми здесь уже не эффективны.

Прочностные свойства металла или твердого раство­ра заданного состава могут существенно изменяться в зависимости от их структурного состояния. Выше уже отмечалось, что измельчение зерна опосо6ствует повы­шению прочностных и пластических характеристик. Уп­рочнению способствует также повышение плотности дис­локаций, создание полигонизованных структур.В деформированных металлах и сплавах, для кото­рых характерно наличие текстуры, механические свойст­ва образцов, вырезанных и растягиваемых при испыта­нии вдоль направления деформации (прокатки, прессования), обычно выше, чем в поперечном направлении.

Влияние выделений избыточных фаз

Выделения избыточных фаз обеспечивают сохранение высокой прочности до предплавильных температур, что лежит в основе разработки жаропрочных сплавов. Степень упрочнения сплава зависит от следующих факторов:

- свойств и структуры основной и избыточных фаз;

- их связи со структурой матрицы;

- формы и размера частиц;

- расстояния между ними;

- характера распределения в матрице.

В общем случае максимальное упрочнение может быть достигнуто в следующих случаях:

- вторая фаза когерентна или полукогерентна матрице;

- дисперсна и равномерно распределена в объеме сплава;

- имеет высокую собственную прочность;

- расстояние между ее частицами мало.

Большая часть этих условий реализуется при дисперсионном и дисперсном упрочнении сплавов. В соответствии с этими механизмами упрочнения различают два вида сплавов- дисперсионно-твердеющие и дисперсно-упрочненные.

Дисперсионное упрочнение, или твердение, достигает­ся при старении (отпуске) в результате распада образо­вавшегося после закалки пересыщенного твердого рас­твора (метастабильной фазы). Аналогичный эффект мож­но получить и другими способами. В частности, в пос­ледние годы все более широко применяется внутреннее окисление, при котором диффундирующий в образец при окислительном отжиге кислород взаимодействует с химически активными легирующими элементами, образуя равномерно распределенные в объеме дисперсные выделения окислов.

Дисперсное упрочнение реализуется в порошковой металлургии, когда к металлу-основе добавляют порошок заранее приготовленной фазы-yпрочнителя, не взаимодействующей с матрицей (например, ThО₂ к вольф­раму). Затем эту смесь порошков подвергают, обработке и получают материал, структура которого состоит из зерен матрицы с равномерно распределенными в ней включениями избыточной фазы. Дисперсионно- и дис­персноупрочненные материалы обладают, как правило, более низкой пластичностью, чем неупрочненная матрица.

Основой механизма упрочнения сплавов за счет частиц из­быточных фаз заключается в том, что эти частицы пересекают плоскости скольжения дислокаций матрицы и препятствуют их перемещению. Если частицы дисперсны, близко расположены друг от друга и когерентны матрице, то дислокации могут проходить через них - происходит «перерезание» частиц (рисунок 11.2а). Если же частицы некогерентны матрице, и достаточно далеки друг от друга, то дислокации «проталкиваются» между ними, оставляя петли вокруг час­тиц (рисунок 11.2б). Напряжение; необходимое для тако­го проталкивания

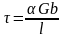, (11.7)

где l – расстояние между частицами.

В первом приближении это напряжение должно соответствовать напряжению течения гетерофазного сплава (с монокристальной матрицей). Зависимость напряжения течения от объемной доли Q некогерентных частиц определяется уравнением

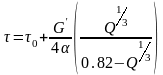, (11.8)

где τ₀ – напряжение течения материала матрицы без выделений;

G′- модуль сдвига избыточной фазы;

α – коэффициент.

Как видно из формулы (11.7), прочностные свойства растут обратно пропорционально расстоянию l между частицами. Происходит это до тех пор, пока l не станет величиной того же порядка, что и минимально возмож­ный радиус изгиба дислокационной линии (150-100 меж­атомных расстояний). При меньших расстояниях между выделениями дислокации могут перемещаться только через них. Это становится возможным при условии хотя бы частичной когерентности структур выделения и мат­рицы, когда определенные плоскости и направления кристаллической решетки матрицы находят плавное продолжение в решетке выделения. Такая ситуация воз­никает обычно на ранних стадиях старения, когда внут­ри твердого раствора образуются зоны Гинье - Престо­на или промежуточные фазы.

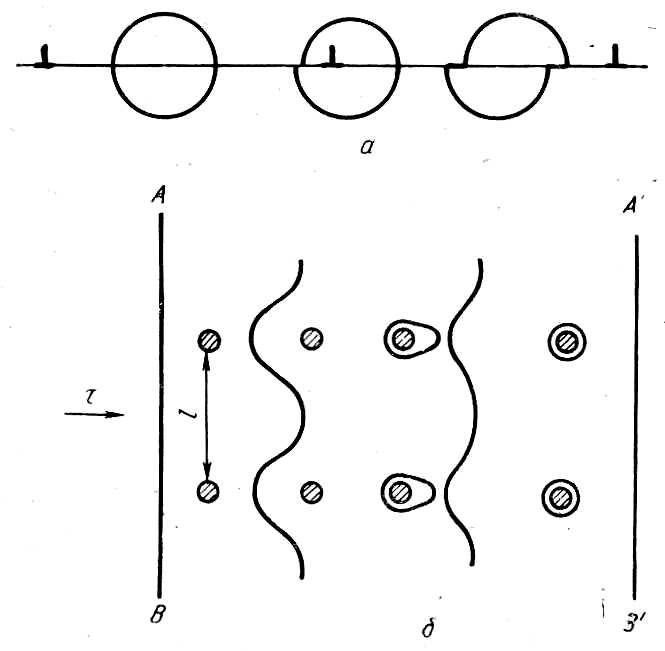
а – перерезание частиц; б – проталкивание между частицами с образованием петель Рисунок – 11.2 Взаимодействие дислокаций с частицами второй фазы

При перерeзании дислокациями выделений упрочнение достигается вследствие целого ряда причин. Движе­нию дислокации препятствует поле упругих напряже­ний вокруг выделения. Для перемещения дислокаций внутри частиц требуются более высокие напряжения, так как их модуль сдвига обычно выше, чем у матрицы. Если выделение имеет упорядоченную структуру, то не­обходимо затратить дополнительную энергию для разу­порядочения в плоскости скольжения. Как видно из схе­мы, приведенной на рисунке 11.2а, после прохождения дисло­кации через частицу образуются новые поверхности раз­дела между ней и окружающей матрицей. Это также требует дополнительного напряжения. Если частицы со средним радиусом r имеют неупорядоченную структуру, то напряжение течения необходимое для перерезания частиц, определяется выражением

, (11.9)

где Q - объемная доля выделений;

γ_s - поверхностная энергия на границе раздела матрица - выделение.

Из рассмотренного следует, что дисперсионное упрочнение может быть обусловлено как обходом, так и перерезанием частиц дислокациями. При дисперсном упрочнении вторая фаза, как правило, некогерентна матрице, а расстояние между отдельными частицами намного боль­ше минимального радиуса изгиба дислокации. Поэтому здесь дислокации не должны проходить через частицы, а максимальная степень упрочнения должна быть меньше. Однако на практике этот вывод подтверждается только при относительно низких температурах, когда в резуль­тате дисперсионного упрочнения действительно можно получить значительно больший относительный прирост прочности, чем при дисперсном упрочнении. В условиях же высоких температур (>0,5-0,6 Т_пл) продукты ста­рения, как правило, становятся уже весьма грубыми (они коагулируют в процессе работы при высокой тем­пературе) и к тому же менее стабильными, чем частицы в дисперсноупрочненных материалах. В результате их высокотемпературное упрочнение более значительно, чем в закаленных и состаренных сплавах.

Частицы избыточных фаз содержатся в структуре многих сплавов, не подвергающихся дисперсионному или дисперсному упрочнению. Они могут образовывать­ся при кристаллизации, выделяться или видоизменять­ся в процессе деформации, отжига и т.д. Такие части­цы по размерам и расстоянию между ними обычно на порядки больше, чем те, которые обеспечивают макси­мальное упрочнение, например при старении или внут­реннем окислении. Двyx- и многофазные сплавы с такими частицами рассматривают как механичес­кие смеси, свойства которых аддитивно складыва­ются из свойств отдельных фаз, составляющих дан­ную смесь. Строго говоря, правило аддитивности должно выполняться только в том случае, если в процессе испытания все фазы принимают одинаковое учас­тие в деформации образца. В реальных сплавах свойст­ва разных фаз обычно существенно различаются. Если, например, основная фаза относительно мягка и пластична, а избыточная - тверда и xpyпкa, то деформация образца осуществляется в основном в результате дефор­мации матрицы и правило аддитивности строго не вы­полняется, хотя, конечно, с увеличением объемной доли твердой фазы прочностные свойства сплава растут, а пластичность падает.

Важное значение имеет характер распределения крупных частиц избыточных фаз в гетерофазныx сплавах. Если они хрупки и располагаются в виде сплошных це­почек по границам зерен, то сплав имеет низкие плас­тичность (δ и ψ близки к нулю) и прочность. Если же они равномерно распределены по объему сплава в виде компактных включений, то механические свойства выше. Компактные (например, сферические) включения второй фазы повышают характеристики предельной прочности и пластичности в сравнении с игольчатыми и пластинчатыми частицами, даже если последние распределены только по телу зерна. Все эти факты можно объяснить большей легкостью зарождения и развития трещин вдоль или вблизи границ зерен, занятых избыточными выделениями, и вытянутых частиц хрупкой фазы.

Выше отмечалось, что частицы из6ыточных фаз, бо­лее хрупкие, чем матрица, снижают характеристики пластичности. Однако в некоторых случаях возможно и повышение пластичности при введении дозированного количества частиц определенной формы благодаря умень­шению длины зародышевых трещин. Та­кой путь повышения пластичности используют, в частно­сти, применительно к тугоплавким металлам с о. ц. к. решеткой. Например, введение в вольфрам определенно­го количества частиц двуокиси тория повышает не только прочность, но и пластичность.

2. Равномерная и локальная деформация. Роль дислокаций в процессах пластического течения металлов и сплавов.

Наименьшая локальная деформация наблюдается в крупных зернах 1 - 3 балла, наибольшая - в группах зерен 5 - 6 баллов, расположенных по границам больших зерен, а также в приграничных областях. Неоднородность деформации приводит к появлению внутренних локальных напряжений, что может привести к появлению микротрещин в условиях эксплуатации и особенно при переменных режимах и гидравлических ударах. [2]

Фактическая локальная деформация много выше исходной начального состояния трубопровода, поэтому несущую способность конструкции необходимо рассматривать с учетом пластической составляющей.

За счет локальной деформации в шейке другие участки краевого элемента, расположенные вне шейки, должны получать меньшие деформации по сравнению с деформациями, которые имели бы место при равномерном деформировании. В то же время смежный элемент, получивший меньшую деформацию, деформируется равномерно, без образования шейки. Если дополнительные растягивающие напряжения, возникающие в элементе, более удаленном от края, не способны вывести этот элемент за пределы устойчивой деформации, то он будет продолжать равномерно деформироваться ( в тангенциальном направлении) и тем затруднит образование шейки в краевом элементе.

Кроме того, малые локальные деформации, которые обычно появляются при хрупком разрушении, позволяют конструктору рассматривать отдельно центробежные и температурные аспекты общей конструктивной проблемы, а затем обобщать их для определения упругопластической зоны. [1]

Однако при вспышке локальной деформации во время появления зародыша ротационной пластичности может происходить разделение зарядов и в первичной системе. В первичной системе скольжения формируется дислокационная лавина. Вследствие одновременного прохождения лавины и диполя образуется бездислокационный канал с переориентированной кристаллической решеткой. Упругие поля дислокационного скопления в голове лавины и дисклинационного диполя на фронте полосы способствуют развитию друг друга.

Билет №6

1. Особенности твердорастворного упрочнения при образовании твердых растворов замещения и внедрения. Аналитическая и графическая формы описания.

По степеням растворимости компонентов различают твердые растворы:

• с неограниченной растворимостью компонентов;

• с ограниченной растворимостью компонентов.

При неограниченной растворимости компонентов кристаллическая решетка компонента растворителя по мере увеличения концентрации растворенного компонента плавно переходит в кристаллическую решетку растворенного компонента.

Для образования растворов с неограниченной растворимостью необходимы:

1. изоморфность (однотипность) кристаллических решеток компонентов;

2. близость атомных радиусов компонентов, которые не должны отличаться более чем на 8…13 %.

3. близость физико-химических свойств подобных по строение валентных оболочек атомов.

При ограниченной растворимости компонентов возможна концентрация растворенного вещества до определенного предела, При дальнейшем увеличении концентрации однородный твердый раствор распадается с образованием двухфазной смеси.

По характеру распределения атомов растворенного вещества в кристаллической решетке растворителя различают твердые растворы:

• замещения;

• внедрения;

• вычитания.

В растворах замещения в кристаллической решетке растворителя часть его атомов замещена атомами растворенного элемента (рис. 4.4 а). Замещение осуществляется в случайных местах, поэтому такие растворы называют неупорядоченными твердыми растворами.

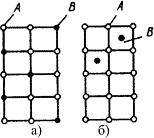
Рис.4.4. Кристаллическая решетка твердых растворов замещения (а), внедрения (б)

При образовании растворов замещения периоды решетки изменяются в зависимости от разности атомных диаметров растворенного элемента и растворителя. Если атом растворенного элемента больше атома растворителя, то элементарные ячейки увеличиваются, если меньше – сокращаются. В первом приближении это изменение пропорционально концентрации растворенного компонента. Изменение параметров решетки при образовании твердых растворов – важный момент, определяющий изменение свойств. Уменьшение параметра ведет к большему упрочнению, чем его увеличение.

Твердые растворы внедрения образуются внедрением атомов растворенного компонента в поры кристаллической решетки растворителя (рис. 4.4 б).

Образование таких растворов, возможно, если атомы растворенного элемента имеют малые размеры. Такими являются элементы, находящиеся в начале периодической системы Менделеева, углерод, водород, азот, бор. Размеры атомов превышают размеры межатомных промежутков в кристаллической решетке металла, это вызывает искажение решетки и в ней возникают напряжения. Концентрация таких растворов не превышает 2-2.5%

Твердые растворы вычитания или растворы с дефектной решеткой. образуются на базе химических соединений, при этом возможна не только замена одних атомов в узлах кристаллической решетки другими, но и образование пустых, не занятых атомами, узлов в решетке.

К химическому соединению добавляют, один из входящих в формулу элементов, его атомы занимают нормальное положение в решетке соединения, а места атомов другого элемента остаются, незанятыми.

2. Роль дислокаций в пластичности и разрушении. Дислокационные механизмы разрушения материалов.

Пластическая деформация происходит в результате скольжения или двойникования. Ранее предполагали, что при скольжении одна часть кристалла сдвигается относительно другой части на целое число периодов как единое целое. Необходимое для этого напряжение получается на несколько порядков выше действительного сдвигового напряжения.

Для железа теоретическое значение сдвигового напряжения МПа, _.

В основу современной теории пластической деформации взяты следующие положения:

• скольжение распространяется по плоскости сдвига последовательно, а не одновременно;

• скольжение начинается от мест нарушений кристаллической решетки, которые возникают в кристалле при его нагружении.

Схема механизма деформации представлена на рис.6.6 а.

В равновесном состоянии дислокация неподвижна. Под действием напряжения экстраплоскость смещается справа налево при незначительном перемещении атомов. Нижняя часть плоскости Р^/S (SR) сместится вправо и совместится с нижним краем экстра- плоскости РQ.

QR- остаточная деформация.

При дальнейшем движении дислокация пройдет всю плоскость скольжения и выйдет на поверхность зерна. При этом верхняя часть зерна сдвинута относительно нижней на один межатомный период решетки (рис. 6.6 б).

При каждом перемещении дислокации на один шаг необходимо разорвать связь только между двумя рядами атомов в плоскости Р^/S, а не между всеми атомами, расположенными выше и ниже плоскости скольжения. Необходимое сдвиговое напряжение при этом мало, равно практически действительному..

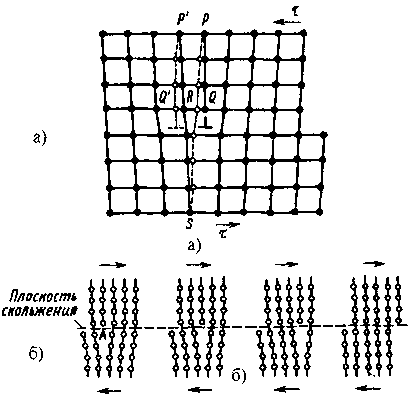
Рис. 6.6. Схема дислокационного механизма пластической деформации а – перемещение атомов при двихении краевой дислокации на одно межатомное расстояние; б – перемещение дислокации через весь кристалл

Разрушение металлов.

Процесс деформации при достижении высоких напряжений завершается разрушением. Тела разрушаются по сечению не одновременно, а вследствие развития трещин. Разрушение включает три стадии: зарождение трещины, ее распространение через сечение, окончательное разрушение.

Различают хрупкое разрушение – отрыв одних слоев атомов от других под действием нормальных растягивающих напряжений. Отрыв не сопровождается предварительной деформацией. Механизм зарождения трещины одинаков - благодаря скоплению движущихся дислокаций перед препятствием (границы субзерен, фазовые границы), что приводит к концентрации напряжений, достаточной для образования трещины. Когда напряжения достигают определенного значения, размер трещины становится критическим и дальнейший рост осуществляется произвольно.

Для хрупкого разрушения характерна острая, часто ветвящаяся трещина. Величина зоны пластической деформации в устье трещины мала. Скорость распространения хрупкой трещины велика - близка к скорости звука (внезапное, катастрофическое разрушение). Энергоемкость хрупкого разрушения мала, а работа распространения трещины близка к нулю.

Различают транскристаллитное разрушение – трещина распространяется по телу зерна, интеркристаллитное – по границам зерен (всегда хрупкое).

Результатом хрупкого разрушения является блестящий светлый кристаллический излом с ручьистым строением. Хрупкая трещина распространяется по нескольким параллельным плоскостям. Плоскость излома перпендикулярна нормальным напряжениям.

Вязкое разрушение – путем среза под действием касательных напряжений. Ему всегда предшествует значительная пластическая деформация.

Трещина тупая раскрывающаяся. Величина пластической зоны впереди трещины велика. Малая скорость распространения трещины. Энергоемкость значительная, энергия расходуется на образование поверхностей раздела и на пластическую деформацию. Большая работа затрачивается на распространение трещины. Поверхность излома негладкая, рассеивает световые лучи, матовая (волокнистый) излом. Плоскость излома располагается под углом.

По излому можно определить характер разрушения.

7,2 Хладноломкость тугоплавких металлов. Роль примесей внедрения в проявлении тепловой хрупкости.

В металлах атомы примесей внедрения (кислород, азот, водород и углерод) располагаются в междоузлиях решетки, которые значительно меньше, чем их атомные диаметры. Это вызывает искажение кристаллической решетки и приводит к изменению механических свойств. Степень влияния примесей внедрения на свойства зависит от их предельной растворимости в металле, типа решетки и характера образующихся соединений; чем меньше растворимость и атомный радиус элемента, тем больше это влияние.

По современным представлениям, примеси внедрения создают так называемые атмосферы Коттрелла, являющиеся препятствием для движущихся дислокаций. Кроме того, выделившись из твердого раствора, примеси скапливаются по границам зерен в виде сегрегаций или избыточных фаз. Из-за высокой хрупкости этих выделений прочность границ снижается, что приводит к возникновению трещин.

Технические чистые металлы IVA (Zr) н VA (V, Nb, Та) групп обычно содержат количество примесей внедрения, меньшее предела их растворимости и представляют разбавленные твердые растворы по отношению к этим примесям. Они пластичны даже при криогенных температурах. Основной причиной хрупкого разрушения таких металлов является высокотемператур­ное насыщение примесями внедрения.

8,1 Разрушение с позиций мгновенного разрыва межатомных связей. Роль пластической деформации в хрупком разрушении.

При рассмотрении хрупкого разрушения Гриффитсом были сделаны следующие допущения:

1 Разрушение происходит на стадии упругой деформации при разрушающем напряжении, меньше предела упругости.

2 Объектом разрушения является пластина единичной толщины, жестко закрепленная с обеих сторон и имеющая зародышевую трещину (рисунок 6.1).

3 Трещина имеет форму эллипса с полуосями, равными с и 2с (рисунок 6.1а). Объем трещины равен объему цилиндра, т.е.V=2π c².

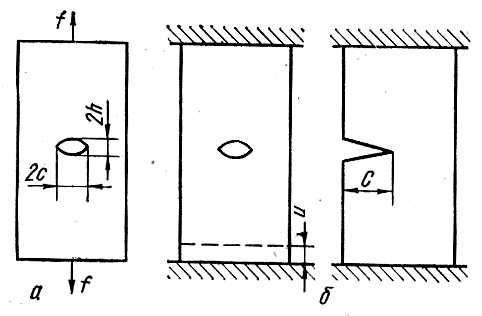
а – свободное нагружение; б – нагружение в фиксированных зажимах Рисунок – 6.1 Различные схемы нагружения

Рассмотрим последовательность процессов, предшествующих разрушению:

1 При упругой деформации ε, запасенная упругая энергия в единице объема пластины без трещины равна работе, затраченной на эту деформацию, при условии, что напряжение на участке. описываемом законом Гука, изменятся от нуля до значения σ_макс.. В таком случае среднее действующее напряжение σ будет равно ½ σ_макс, а работа. равная произведению силы на пройденный путь

А= ½ σ ε =½ σ²/Е, (6.1)

где ε = σ/Е.

2 Предполагается, что при внезапном (очень высокой скорости) возникновении в теле трещины длиной 2с под прямым углом к направлению действующего напряжения σ высвобождается часть запасенной упругой энергии в зоне эллипсоидальной трещины, пропорциональная объему трещины V=2π c². Упругая энергия пластины при этом уменьшится на величину W

W = ½ σ²/Е 2π c² = π σ² c²/ Е, (6.2)

3 При возникновении трещины образуются две новые поверхности с удельной поверхностной энергией γ_s, что приведет к увеличению внутренней энергии пластины на величину U, пропорциональную площади поверхности трещины равную 2с, так как толщина пластины принята за единицу:

U = 4 γ_s с. (6.3)

Площадь трещины определяется произведением длины трещины 2с на толщину, равную по условию задачи единице.

4 Энергетический баланс при возникновении трещины равен разнице между энергией, затраченной на образование трещины W и энергией, способствующей увеличению внутренней поверхностной энергии U. Затраченная энергия считается отрицательной, а приобретенная – положительной.

ΔU = U – W = 4 γ_s с - π σ²/Е c². (6.4)

5 В зависимости от соотношения между U, W и ΔU баланс может быть положительным и отрицательным.

5.1 Если ΔU будет больше нуля, то для увеличения трещины необходим подвод энергии, что противоречит законам хрупкого разрушения. Следовательно, баланс энергий должен быть отрицательным.

5.2 Если ΔU меньше нуля, общая энергия пластины уменьшается, и трещина развивается самопроизвольно за счет упругой энергии пластины.

Условие перехода к нестабильному росту трещины при данном внешнем напряжении σ определится при равенстве нулю первой производной от dΔU по dc:

dΔU/ dc = 0 или 4 γ_s - 2π σ²/Е c = 0, (6.5)

т.е.

σ = ( 2Е γ_s/π с)^1/2 (6.6)

Полученное выражение характеризует критическое условие начала нестабильного распространения хрупкой трещины и означает следующее:

Чем больше длина трещины, тем меньшее напряжение требуется для ее распространения. Однако на практике разрушающие напряжения, на несколько порядков меньше рассчитанных по данной формуле. Исключение составляют идеально хрупкие материалы ( стекла ), для которых пластическая деформация полностью отсутствует. Отсюда следует, что для большинства металлов и сплавов основная причина расхождения расчетного и действительного разрушающего напряжения состоит в том, что в модели Гриффитса не учитывается возможность развития при хрупком разрушении пластической деформации. Следовательно, его предположение о внезапном (мгновенном, т.е. время слишком мало, чтобы могла развиться пластическая деформация) не верно.

Орован, проанализировав большое количество экспериментальных результатов, пришел к заключению о том, что часть недостающей энергии тратится на пластическую деформацию вблизи вершины хрупкой трещины. Как любая пластическая деформация, она осуществляется путем движения дислокаций в сравнительно тонком слое толщиной 10 мкм - 0,1 мм, в котором напряжения достигают величины, большей макроскопического предела текучести. При этом структурное состояние в этом слое эквивалентно структурному состоянию того же самого материала, подвергнутого статической деформации в несколько процентов. Орован предложил в формуле (6.6) вместо поверхностной энергии γs использовать сумму поверхностной энергии и энергии, затраченной на пластическую деформацию, т.е. γs + γр, после чего расчетные и действительные значения разрушающего напряжения стали максимально близки.

8,2 Роль пластической деформации при распространении хрупкой и вязкой трещины

В окрестности хрупкой трещины развивается небольшая пластическая деформация, которая управляет процессом ее роста. Лишь при большой скорости трещины пластическая деформация может представлять собой сопутствующее явление.

Процесс роста "вязкой" трещины невозможен без пластической деформации, которая достигает значительной величины.

8 билет 2 вопрос,16 по списку

С практической точки зрения хрупкое разрушение гораздо важнее, чем вязкое, так как это наиболее опасный вид катастрофического разрушения. В отличие от вязкого хрупкое разрушение как и упругая деформация, достаточно хорошо описываются математическими моделями, на основании которых с определенной степенью приближения выводятся основные закономерности взаимосвязи процессов нагружения и деформирования. Впервые физические основы теории хрупкого разрушения разработаны Гриффитсом.

При рассмотрении хрупкого разрушения Гриффитсом были сделаны следующие допущения:

1 Разрушение происходит на стадии упругой деформации при разрушающем напряжении, меньше предела упругости.

2 Объектом разрушения является пластина единичной толщины, жестко закрепленная с обеих сторон и имеющая зародышевую трещину (рисунок 6.1).

3 Трещина имеет форму эллипса с полуосями, равными с и 2с (рисунок 6.1а). Объем трещины равен объему цилиндра, т.е.V=2π c².

4с 2с

а – свободное нагружение; б – нагружение в фиксированных зажимах Рисунок – 6.1 Различные схемы нагружения

Рассмотрим последовательность процессов, предшествующих разрушению:

1 При упругой деформации ε, запасенная упругая энергия в единице объема пластины без трещины равна работе, затраченной на эту деформацию, при условии, что напряжение на участке. описываемом законом Гука, изменятся от нуля до значения σ_макс.. В таком случае среднее действующее напряжение σ будет равно ½ σ_макс, а работа. равная произведению силы на пройденный путь

А= ½ σ ε =½ σ²/Е, (6.1)

где ε = σ/Е.

2 Предполагается, что при внезапном (очень высокой скорости) возникновении в теле трещины длиной 2с под прямым углом к направлению действующего напряжения σ высвобождается часть запасенной упругой энергии в зоне эллипсоидальной трещины, пропорциональная объему трещины V=2π c². Упругая энергия пластины при этом уменьшится на величину W

W = ½ σ²/Е 2π c² = π σ² c²/ Е, (6.2)

3 При возникновении трещины образуются две новые поверхности с удельной поверхностной энергией γ_s, что приведет к увеличению внутренней энергии пластины на величину U, пропорциональную площади поверхности трещины равную 2с, так как толщина пластины принята за единицу:

U = 4 γ_s с. (6.3)

Площадь трещины определяется произведением длины трещины 2с на толщину, равную по условию задачи единице.

4 Энергетический баланс при возникновении трещины равен разнице между энергией, затраченной на образование трещины W и энергией, способствующей увеличению внутренней поверхностной энергии U. Затраченная энергия считается отрицательной, а приобретенная – положительной.

ΔU = U – W = 4 γ_s с - π σ²/Е c². (6.4)

5 В зависимости от соотношения между U, W и ΔU баланс может быть положительным и отрицательным.

5.1 Если ΔU будет больше нуля, то для увеличения трещины необходим подвод энергии, что противоречит законам хрупкого разрушения. Следовательно, баланс энергий должен быть отрицательным.

5.2 Если ΔU меньше нуля, общая энергия пластины уменьшается, и трещина развивается самопроизвольно за счет упругой энергии пластины.

Условие перехода к нестабильному росту трещины при данном внешнем напряжении σ определится при равенстве нулю первой производной от dΔU по dc:

dΔU/ dc = 0 или 4 γ_s - 2π σ²/Е c = 0, (6.5)

т.е.

σ = ( 2Е γ_s/π с)^1/2 (6.6)

8 билет 16 вопрос