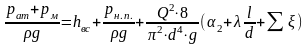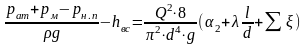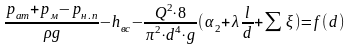3.2. Определение минимального диаметра всасывающего трубопровода

Определим минимальный диаметр всасывающего трубопровода из условия отсутствия кавитации.

Дано:

Подача насоса Q=610^-3м³/с ; длина трубопровода l=30м; высота всасывания =2,0 м; коэффициент сопротивления фильтра _ф= 6,2; коэффициент сопротивления поворота _пов = 1,32; давление насыщенного пара ацетона при температуре 4С - р_н.п. = 2410³ Па; абсолютная шероховатость поверхности трубопровода _э = 0,5 мм; атмосферное давление равно 10⁵Па, манометрическое давление на поверхности жидкости во всасывающем резервуаре равно 0,06 МПа.

Последовательность решения задачи

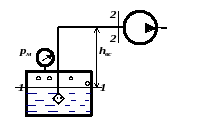
Рис.10. К определению минимального диаметра трубопровода.

Минимальный диаметр определяем из условия, что давление в сечении 2-2 равно давлению насыщенного пара. Тогда уравнение Бернулли для сечений 1-1 и

2-2 имеет вид:

(39)

Преобразуем уравнение Бернулли следующим образом: в левой части сгруппируем слагаемые, не зависящие от диаметра, а в правой части - зависящие от диаметра.

(40)

Задача заключается в определении диаметра из уравнения (40). Поскольку при разных значениях диаметра может быть различный режим движения в трубопроводе (Re=d/), и коэффициент гидравлического трения  зависит от диаметра сложным образом: =64/Re при ламинарном режиме и  =0,11(68/Re+ _э /d)^0,25 при турбулентном режиме, уравнение (40) в общем случае является трансцендентным. Трансцендентным называется уравнение, которое не решается алгебраическими методами. Такие уравнения решаются графическим способом или численными методами с помощью ЭВМ.

Графический метод решения уравнения (40).

Обозначим:

Задается несколькими значениями диаметра d, вычисляем значение функции f (d) и строим график этой функции. Далее определяем диаметр в точке пересечения графика функции с осью х. Результаты расчётов приведены в таблице 2, на рисунке 11.

Таблица 2. Определение минимального диаметра всасывающего трубопровода.

Определение минимального диаметра всасывающего трубопровода
Абсол. шероховатость м	0,0005	0,0005	0,0005	0,0005	0,0005	0,0005
Кинемат. коэф. вязкости , м2/c	3,10E-01	3,10E-01	3,10E-01	3,10E-01	3,10E-01	3,10E-01
Плотность жидкости , кг/м3	792	792	792	792	792	792
Расход жидкости Q, м3/с	0,006	0,006	0,006	0,006	0,006	0,006
Высота всасывания H1, м	2	2	2	2	2	2
Длина трубопровода l1, м	30	30	30	30	30	30
Диаметр трубопровода d1, м	0,04	0,08	0,12	0,16	0,2	0,24
Cумма коэф.местных.сопротивлений	7,54	7,54	7,54	7,54	7,54	7,54
Давление избыточное в сеч н-н, МПа.	0,06	0,06	0,06	0,06	0,06	0,06
Давление насыщенного пара, Па	24000	24000	24000	24000	24000	24000
Число Рейнольдса Re1	5,69E+02	2,85E+02	1,90E+02	1,42E+02	1,14E+02	9,49E+01
Коэффициент трения λ1	0,112	0,225	0,337	0,450	0,562	0,674
Коэффициент Кориолиса	2	2	2	2	2	2
Потери напора h1	145,54	9,10	1,80	0,57	0,23	0,11
Скоростной напор	3,17	0,20	0,04	0,01	0,01	0,00
f(d)	133,19	-6,23	-13,69	-14,94	-15,28	-15,41

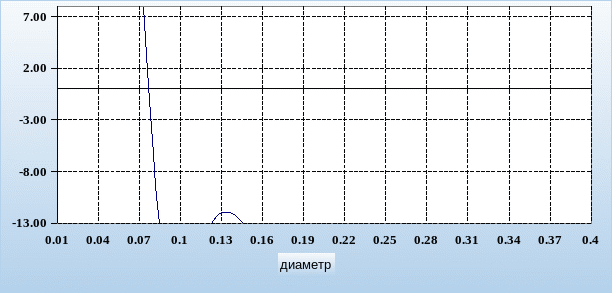
Рис.11. Определение минимального диаметра всасывающего трубопровода.

На пересечении графика функции f(d) с осью диаметров получаем точку, абсцисса которой равна 85 мм. Это и есть искомое минимальное значение диаметра трубопровода из условия отсутствия кавитации: d_min = 85 мм. Поскольку заданное значение диаметра равно 140мм. Минимальное значение диаметра (85мм) меньше диаметра всасывающего трубопровода (140мм) значит кавитации нет.

.3.4. Регулирование подачи центробежного насоса