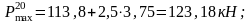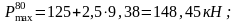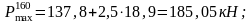- •1 Методика расчета пути
- •2 Расчет пути под действием вертикальных сил
- •2.1 Учет динамических воздействий
- •2.2 Расчет напряжений в элементах верхнего строения пути
- •2.3 Расчет напряжений на основной площадке земляного полотна
- •3 Расчет бесстыкового пути на прочность и устойчивость
- •3.1 Допускаемое изменение температуры по условиям обеспечения прочности подошвы рельса и стыков на разрыв
- •3.2 Допускаемое изменение температуры рельса по условиям устойчивости пути
- •3.3 Определение границ температурного интервала закрепления рельсовых плетей

Содержание
Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1 Методика расчета пути . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
2 Расчет пути под действием вертикальных сил . . . . . . . . . . . . . . . . . . . . . . . . 7
2.1 Учет динамических воздействий . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.2 Расчет напряжений в элементах верхнего строения пути . . . . . . . . 13
2.3 Расчет напряжений на основной площадке земляного полотна . . . 17
3 Расчет бесстыкового пути на прочность и устойчивость . . . . . . . . . . . . . . . 27
3.1 Допускаемое изменение температуры по условиям обеспечения прочности подошвы рельса и стыков на разрыв . . . . . . . . . . . . . . . . . . .27
3.2 Допускаемое изменение температуры рельса по условиям устойчивости пути . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
3.3 Определение границ температурного интервала закрепления рельсовых плетей . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
Заключение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
Список использованной литературы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
Введение
Железнодорожный путь – сложная техническая система, предназначенная для осуществления движения поездов, в виде комплекса расположенных в полосе отвода линейных и инженерных сооружений, и обустройств, образующих дорогу с рельсовой колеей, направляющей колеса подвижного состава.
От технического состояния пути зависит непрерывность и безопасность движения поездов, объемы перевозок, а также эффективность использования подвижного состава.
Комплексные расчеты прочности, устойчивости, долговечности и экономичности конструкции пути при заданных эксплуатационных и природно-климатических условиях, его состоянии и сопротивляемости различным воздействиям дают возможность определить напряженно-деформированное состояние, степень прочности, устойчивости (степень надежности), долговечности (прогнозируемые сроки службы) и экономичности пути, и элементов, его составляющих. В результате сравнения получаемых из расчетов характеристик с их рекомендуемыми и допускаемыми значениями, а также сравнения с другими вариантами конструкции пути определяется оптимальный вариант. Указанными расчетами решается также обширный круг задач по определения допускаемых скоростей движения подвижного состава; в первую очередь это относится к подвижному составу, ранее не обращавшемуся на рассматриваемом участке сети. Условия обращения новых типов подвижного состава и сферы применения новых конструкций пути устанавливаются на основе экспериментальных исследований и данных эксплуатации на опытных участках.
В данной курсовой работе был выполнен расчеты железнодорожного пути на прочность и устойчивость.
1 Методика расчета пути
От подвижной поездной нагрузки и температуры верхнее строение пути испытывает воздействие вертикальных, поперечных и продольных знакопеременных сил, вызывающих напряжения и деформации во всех его элементах.
В соответствии с
Инструкцией по расчету пути на прочность
определяют напряжения в таких элементах
верхнего строения пути, как кромочные
напряжения в рельсах,
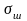 - напряжения под подкладкой,
- напряжения под подкладкой,
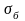 - напряжения в балласте под шпалой,
- напряжения в балласте под шпалой,
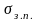 - напряжения на основной площадке
земляного полотна.
- напряжения на основной площадке
земляного полотна.
В основу расчетов пути на прочность и устойчивость приняты следующие предпосылки и допущения:
1 Железнодорожный путь рассчитывается так, как будто он состоит из одного рельса и половины шпалы, подвижная нагрузка также действует на один рельс, поперечные колебания учитываются эмпирическими коэффициентами.
2 Рельс рассматривается как балка бесконечной длины на сплошном однородном упругом основании.
3 Вертикальные силы считаются приложенными в центре головки рельса.
4 Влияние действия горизонтальных поперечных сил и эксцентриситет приложенной вертикальной нагрузки на рельс учитывается коэффициентом, зависящим от рода подвижного состава и плана пути.
Путь и подвижной состав считаются исправными, если их состояние отвечает требованиям ПТЭ.
6 Полагается, что колеса подвижного состава не отрываются от рельса, а траектория их центра тяжести при движении описывает неровности без удара.
7 Упругая реакция основания является двухсторонней, линейно зависящей от осадки основания (гипотеза Винклера).
8 Характеристики пути (модуль упругости подрельсового основания и др.) считаются детерминированными.
9 Метод расчета пути на прочность- статический.
10 В расчетное сечение устанавливается колесо с максимальной нагрузкой, влияние соседних колес учитывается при условии, что они создают среднюю нагрузку.
11 Продольная сила, возникающая при изгибе рельса, не учитывается.
12 Принят закон независимости действия сил.
13 Максимальная вертикальная сила от колеса определяется из условия, что вероятность ее превышения будет равна 0,0062 (соответственно вероятность не превышения взятой в расчет максимальной величины вертикальной силы составит 0,9937).
2 Расчет пути под действием вертикальных сил
2.1 Учет динамических воздействий
В соответствии с допущением о том, что максимальная сила случайна, в 0,6% случаев она может превысить взятое в расчет значение:
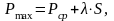 (2.1)
(2.1)
где 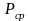 - среднее значение нагрузки колеса на
рельс, кН;
- среднее значение нагрузки колеса на
рельс, кН;
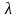 -
нормирующий множитель, приводящий
максимальное значение расчётной силы
к величине, вероятность непревышения
которой составляет 0,994 при
=2,5;
-
нормирующий множитель, приводящий
максимальное значение расчётной силы
к величине, вероятность непревышения
которой составляет 0,994 при
=2,5;
S – суммарное среднее квадратичное отклонение дополнительных динамических сил, кН.
Для современного
подвижного состава (без учетов паровозов)
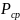 находят по формуле:
находят по формуле:
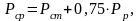 (2.2)
(2.2)
где 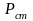 - статическая нагрузка колеса на рельс,
кН;
- статическая нагрузка колеса на рельс,
кН;
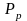 - дополнительная динамическая нагрузка,
вызванная колебаниями рессор, кН.
- дополнительная динамическая нагрузка,
вызванная колебаниями рессор, кН.
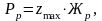 (2.3)
(2.3)
где 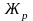 - жесткость рессорного комплекта, 0,91
МН/м;
- жесткость рессорного комплекта, 0,91
МН/м;
 - максимальный прогиб рессор расчетного
экипажа, м, определяемый по формуле:
- максимальный прогиб рессор расчетного
экипажа, м, определяемый по формуле:
 (2.4)
(2.4)
Средние значения дополнительных инерционных сил, возникающих от наличия неровностей на пути и на колесах, близки к нулю и поэтому не учитываются в расчете.
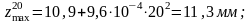
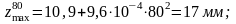
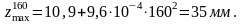
Определяем дополнительную динамическую нагрузку, вызванную колебаниями рессор:
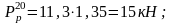
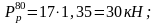
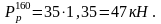
Находим среднее значение нагрузки колеса на рельс:
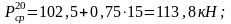
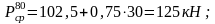
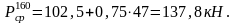
Суммарное среднее квадратическое отклонение от композиции всех динамических сил в соответствии с теорией вероятности равно:
 (2.5)
(2.5)
Среднее квадратическое отклонение каждой из дополнительных динамических сил зависит от:
- колебания рессор
 (2.6)
(2.6)
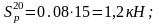
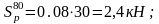
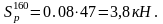
- наличия неровностей в пути:
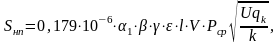 (2.7)
(2.7)
где 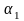 - коэффициент, учитывающий влияние
величины колеблющейся массы пути на
железобетонном подрельсовом основании
по сравнению с путем на деревянных
шпалах, 0,843;
- коэффициент, учитывающий влияние
величины колеблющейся массы пути на
железобетонном подрельсовом основании
по сравнению с путем на деревянных
шпалах, 0,843;
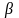 - коэффициент, учитывающий тип рельсов,
(Р65
=0,75);
- коэффициент, учитывающий тип рельсов,
(Р65
=0,75);
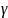 -
коэффициент, учитывающий влияние рода
балласта на образование динамической
неровности на пути (для щебня
=1);
-
коэффициент, учитывающий влияние рода
балласта на образование динамической
неровности на пути (для щебня
=1);
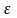 - коэффициент влияния материала рельсовых
опор (дерево, железобетон) на уклон
динамической неровности пути (для
железобетона
=0,332);
- коэффициент влияния материала рельсовых
опор (дерево, железобетон) на уклон
динамической неровности пути (для
железобетона
=0,332);
 - расстояние между осями шпал (или опор
рельсов),м;
- расстояние между осями шпал (или опор
рельсов),м;
V – скорость движения поезда, м/с;
U– модуль упругости подрельсового основания, на кривых 167 Мпа, на прямых 150 Мпа;
 - нагрузка необрес. массы на рельс,
19,25кН;
- нагрузка необрес. массы на рельс,
19,25кН;
К –коэффициент относительной жесткости подрельсового основания и рельса, на кривых 0,01536 см-1, на прямых 0,01578 см-1 при приведенном износе 6мм.
На прямых:

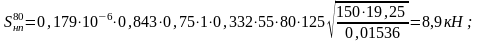
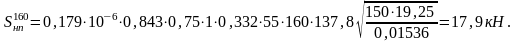
На кривых:
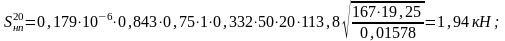
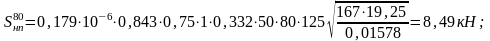

- наличия непрерывных неровностей на колесах
 (2.8)
(2.8)
где  - отношение массы колеса к суммарной
массе колеса и пути, равно 0,365;
- отношение массы колеса к суммарной
массе колеса и пути, равно 0,365;
d – диаметр колеса по кругу катания, 125 см.
На прямом участке:
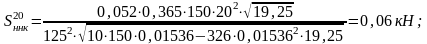
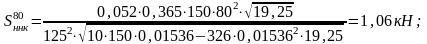
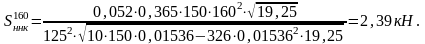
На кривом участке:
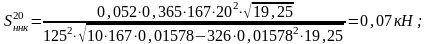
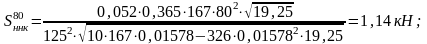
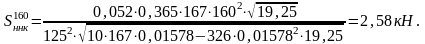
- наличия изолированных неровностей на колесах
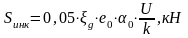 (2.9)
(2.9)
где  - дополнительный максимальный прогиб
рельса, отнесенный к единице глубины
неровности, максимальное его значение
равно 1,47 см;
- дополнительный максимальный прогиб
рельса, отнесенный к единице глубины
неровности, максимальное его значение
равно 1,47 см;
е0 – расчетная глубина изолированной неровности на колесе, принимаемая равной для локомотивов и мотор-вагонного подвижного состава при подшипниках качения 0,047 см.
На прямом участке:

На кривом участке:
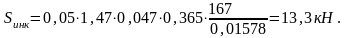
Находим суммарное среднее квадратическое отклонение от композиции всех динамических сил:
На прямом участке:

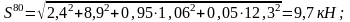
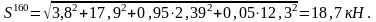
На кривом участке:
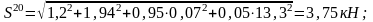
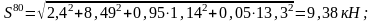

Находим максимальную силу:
На прямом участке:
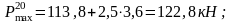
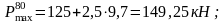
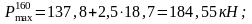
На кривом участке: