
- •1.Тепловое излучение. Проблемы излучения абсолютно черного тела.
- •2. Орбитальный момент электрона. Гиромагнитное отношение.
- •1.Элементарная боровская теория водородного атома.
- •2. Нормальный эффект Зеемана
- •2.Внутренний и внешний фотоэффект
- •2.Квантовая гипотеза. Фотоны.
- •2.Соотношение неопределенности Гейзенберга
- •7 Билет
- •1. Уровни энергии в планетарной модели атома. Постулаты бора
- •2) Внутренний момент электрона
- •15 Билет
- •2. Движение свободной частицы
- •16 Билет
- •1.Корпускулярно-волновой дуализмсвойств веществ...
- •2. Эффект Комптона
- •17 Билет
- •1. Стационарное состояние. Волновая ф-ия.Усл-ие нормиповки
- •18 Билет
- •1. Операторы важнейших физ-их величин оператором пространственной координаты
- •21 Билет
- •2. Опыты Франка Герца
- •22 Билет
- •1.Закон смещения Вина
- •2. Аномалтный эффект Зеемана
- •23 Билет
- •1. Классическая теория изл-ия черного тела. Законы Вина
- •24 Билет
- •1. Закон Кирхгофа. Амплтуда вероятности.
- •2. Системы тождественных частиц
2) Внутренний момент электрона
Чётное число проекций момента возможно только в том случае, если его абсолютная величина имеет полуцелое значение. В 1925 г. Уленбек и Гаудсмит предложили гипотезу спина, иливнутреннего момента электрона. По аналогии с l введём безразмерный вектор s, абсолютная величина которого может быть равна нулю и положительному целому либо полуцелому числу:
(2.1) s = 0, 1/2, 1, 3/2, 2, 5/2, 3, …
Целому значению s, как и l, соответствует нечётное число проекций, среди которых обязательно присутствует компонента, равная нулю. В случае полуцелого спина набор проекций получается чётным, и нулевой компоненты нет. Результаты опытов Штерна и Герлаха для перечисленных выше элементов получают своё объяснение при s = ½.
Гиромагнитное отношение электрона γe в случае внутреннего момента вдвое больше, чем для орбитального:
(2.2) μ = –2μ0s.
Спин — новая характеристика частицы, наряду с массой и зарядом. Он является более фундаментальной величиной, чем орбитальный момент, который может принять разные значения, в зависимости от условий эксперимента. Спин любой частицы всегда сохраняет своё значение, меняться может лишь его проекция на выбранное направление.
Итак, внутренний механический момент системы выражается через безразмерный вектор s:
M = ħ·s,
квадрат модуля которого равен |s|² = s(s+1).
Для электрона
(2.3) s = ½.
Спину s соответствует набор проекций, аналогичный (12.3.5):
![]()
но s может принимать полуцелое значение и тогда среди чисел ряда (2.4) отсутствует нуль.
В отличие от орбитального момента, спин любой системы частиц ограничен. Поэтому при переходе в классическую область он стремится к нулю вместе с постоянной Планка. Таким образом, спин является чисто квантовым понятием, не имеющим аналога в классической механике.
№10
1) Тепловое излучение тел, находящихся в термодинамическом равновесии, называется равновесным излучением или температурным. В термодинамическом равновесии тепловое излучение, тел компенсируется поглощением такого же количества энергии падающего на него излучения.
Для
спектральной характеристики теплового
излучения тела вводится понятие
лучеиспускательной способности тела,
которую называют также просто
испускательной способностью или
спектральной плотностью энергетической
светимости
 .
.
Лучеиспускательной
способностью
тела называется энергия электромагнитного
излучения
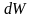 изл
, испускаемого
с единицы площади поверхности тела за.
единицу времени в интервале частот от
изл
, испускаемого
с единицы площади поверхности тела за.
единицу времени в интервале частот от
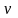 до
до
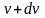 .
Таким образом
.
Таким образом
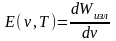 .
(1.1)
.
(1.1)
Лучеиспускательная способность в системе СИ выражается в Дж/м2.
Для
спектральной характеристики поглощения
электромагнитных волн телом вводится
понятие поглощательной
способности
тела
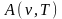 .
Поглощательная способность показывает,
какая доля энергии
,
падающей на единицу площади поверхности
тела за единицу времени в интервале
частот от
до
поглощается телом, т.е.
.
Поглощательная способность показывает,
какая доля энергии
,
падающей на единицу площади поверхности
тела за единицу времени в интервале
частот от
до
поглощается телом, т.е.
 .
(1.2)
.
(1.2)
Как
поглощательная, так и лучеиспускательная
способности твердого тела зависят от
частоты
излучаемых или поглощаемых волн, от
температуры тела, от его химического
состава и состояния поверхности. Если
тело полностью поглощает падающую на
него энергию электромагнитного излучения
при любой температуре и для всех частот,
то такое тело называют абсолютно черным.
Поглощательная способность абсолютно
черного тела по определению равна
единице
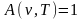 .
.
Лучеиспускательная
способность абсолютно черного тела
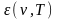 зависит только от частоты
и
абсолютной температуры. Реальные тела
не являются абсолютно черными. Достаточно
хорошим приближением абсолютно черного
тела являются сажа, платиновая чернь,
черный бархат. Наиболее близкой моделью
абсолютно черного тела является
поверхность малого отверстия в
непрозрачной стенке замкнутой полости.
зависит только от частоты
и
абсолютной температуры. Реальные тела
не являются абсолютно черными. Достаточно
хорошим приближением абсолютно черного
тела являются сажа, платиновая чернь,
черный бархат. Наиболее близкой моделью
абсолютно черного тела является
поверхность малого отверстия в
непрозрачной стенке замкнутой полости.
Законы Вина Следующий шаг в нахождении явного вида функции Кирхгофа был предпринят В. Вином в 1893 году, который рассмотрел задачу об адиабатическом сжатии излучения абсолютно черного тела в цилиндрическом сосуде с подвижным зеркальным поршнем и зеркальными стенками. В результате он получил следующее выражение для функции Кирхгофа:
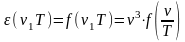 (1.9)
(1.9)
где
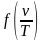 - некоторая
неизвестная в явном виде функция.
- некоторая
неизвестная в явном виде функция.
Хотя сам В. Вин не установил явного вида функции, однако, из формулы Вина (1.9) вытекает закон Стефана-Больцмана.
Из опытов было известно, что зависимость лучеиспускательной способности абсолютно черного тела от частоты при различных температурах имеет вид, показанный на рисунке 1.3.
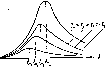
Рис. 1.3
Из
этого рисунка видно, что с ростом
температуры увеличивается максимальное
значение лучеиспускательной способности
абсолютно черного тела. Кроме того, сам
максимум лучеиспускательной способности
черного тела смещается с ростом
температуры в сторону более высоких
частот. Формула В.Вина позволила
сформулировать эти явления в виде
законов Вина. При данной температуре
частота излучения
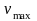 ,
на которую приходится максимум
лучеиспускательной способности абсолютно
черного тела легко определяется из
условия равенства нулю частной производной
от функции Кирхгофа:
,
на которую приходится максимум
лучеиспускательной способности абсолютно
черного тела легко определяется из
условия равенства нулю частной производной
от функции Кирхгофа:
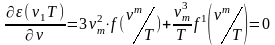 . (1.10)
. (1.10)
Из последнего равенства следует
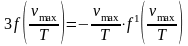
Окончательно получаем закон смещения Вина
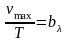 ,
(1.11)
,
(1.11)
который гласит, что частота соответствующая максимальному значению лучеиспускательной способности абсолютно черного тела, прямо пропорциональна его абсолютной температуре.
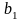 -
постоянная величина, зависящая от явного
вида функции Вина
-
постоянная величина, зависящая от явного
вида функции Вина
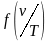 .
Обычно, закон смещения Вина записывают
через длину волны излучения
.
Обычно, закон смещения Вина записывают
через длину волны излучения
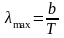 (1.12)
(1.12)
-
длина волны, на которую приходится
максимум лучеиспускательной способности
абсолютно черного тела с ростом
температуры смещается в сторону коротких
длин волн. Постоянная
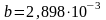 мК
носит название постоянной Вина,
определяется опытным путем.
мК
носит название постоянной Вина,
определяется опытным путем.
Из формулы Вина (1.9) и закона смещения Вина (1.11) следует, что максимум лучеиспускательной способности абсолютно черного тела прямо пропорционален пятой степени абсолютной температуры:
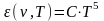 .
(1.13)
.
(1.13)
Последнее
утверждение носит название второго
закона Вина, где
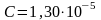 Вт/(м3К5)-
постоянная второго закона Вина.
Вт/(м3К5)-
постоянная второго закона Вина.
Формула Рэлея-Джинса Для нахождения среднего значения энергии гармонического осциллятора Рэлей и Джинс воспользовались классическим законом о равновероятном распределении энергии по степеням свободы осцилляторов, находящихся в термодинамическом равновесии, Из, курса классически статистической физики известно, что на одну степень свободы колебательного движения в среднем приходится энергия равная
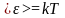
Подставляя эту энергию в формулу (1.14) окончательно получаем формулу Рэлея и Джинса в виде
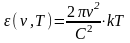 .
(1.15)
.
(1.15)
О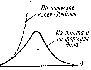 днако,
формула Рэлея и Джинса достаточно хорошо
согласовывалась с опытом только в
области низких частот (рис. 1.4).
днако,
формула Рэлея и Джинса достаточно хорошо
согласовывалась с опытом только в
области низких частот (рис. 1.4).
Рис. 1.4
В области же высоких частот (коротких длин волн) формула Рэлея и, Джинса резко расходится с экспериментальными значениями . Это значительное расхождение теории и опыта при высоких частотах получило название «ультрафиолетовой катастрофы». Кроме того, энергетическая светимость абсолютно черного тела на основе представлений Рэлея и Джинса оказалась равной
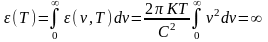
Таким
образом, формула Рэлея и Джинса находилась
в противоречии с законом Стефана-Бoльцмана,
согласно которому
 .
Но, не следует думать, что работы Рэлея
и Джинса оказались бесплодными. Они
показали, что последовательное применение
представлений классической физики
к исследованию теплового излучения не
позволяет объяснить наблюдаемые на
опыте закономерности.
.
Но, не следует думать, что работы Рэлея
и Джинса оказались бесплодными. Они
показали, что последовательное применение
представлений классической физики
к исследованию теплового излучения не
позволяет объяснить наблюдаемые на
опыте закономерности.
2) Квантовые числа. Общее решение уравнения Шредингера (1.3) записывается в виде
Ψ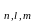 (r,
(r,
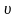 ,φ)
= Rn,l(r) θl,ml
(υ)Ф ml
(φ),
,φ)
= Rn,l(r) θl,ml
(υ)Ф ml
(φ),
где
Rn,l
(r)
—
радиальная волновая функция, зависящая
только от
r(n
и l
— целые числа), функция в
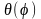 имеет
два целочисленных
индекса: l
и ml
функция Ф
(φ)
—
один целочисленный индекс
ml.
имеет
два целочисленных
индекса: l
и ml
функция Ф
(φ)
—
один целочисленный индекс
ml.
Целое число n, называемое главным квантовым числом, совпадает с номером уровня энергии, определяя энергию электрона в атоме; оно может принимать только целые положительные значения:
Целые числа l и ml представляют собой орбитальное и магнитное квантовые числа.
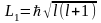
(определяет модуль момента импульса электрона) и Llz= ħ·ml. (определяет проекцию момента импульса электрона на направление Z внешнего магнитного поля).
Оказывается, что решения удовлетворяют стандартным условиям для значений l, не превышающих n-1. Следовательно, 1 при заданном п может принимать значения
l = 0, 1, 2, 3, …,n-1, т. е. всего п значений.
Так как
проекция вектора не может быть больше
модуля этого
вектора, то
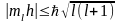 ,
т. е. максимально возможное
значение |ml|=l.
Следовательно, при
заданном l
магнитное
квантовое
число ml
может принимать 2l+1
различных значений:
,
т. е. максимально возможное
значение |ml|=l.
Следовательно, при
заданном l
магнитное
квантовое
число ml
может принимать 2l+1
различных значений:
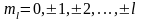
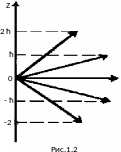
Состояния, соответствующие возможным значениям орбитального квантового числа l, обозначают буквами: для l = 0, 1, 2, 3,... используют буквы s, p, d, f,… и далее по алфавиту. Например, состояние, характеризующееся l = 0, называют s -состоянием, а электрон в этом состоянии — s -электроном. Значение главного квантового числа указывают перед условным обозначением орбитального квантового числа. Например, электроны в состоянии с n = 2, l = 0 и l = 0 и l обозначают соответственно символами 2s и 2р.
Физический смысл магнитного квантового числа можно понять, учитывая, что момент импульса (механический орбитальный момент) электрона L есть вектор; тогда (рис.1.2) величина Llz=ħml определяет проекцию этого вектора на ось 2 (на рисунке рассмотрено d -состояние).
Хотя
энергия электрона (1.5) и зависит только
от главного квантового
числа n,
но каждому собственному значению Еn
(кроме
Е1
соответствует
несколько собственных функций
 отличающихся
значениями l
и ml.
Следовательно, атом водорода может
иметь одно и то же значение энергии,
находясь в нескольких
различных состояниях. Состояния с
одинаковой энергией называют
вырожденными,
а
число состояний с одинаковой энергией
— кратностью
вырождения.
отличающихся
значениями l
и ml.
Следовательно, атом водорода может
иметь одно и то же значение энергии,
находясь в нескольких
различных состояниях. Состояния с
одинаковой энергией называют
вырожденными,
а
число состояний с одинаковой энергией
— кратностью
вырождения.
Так как при данном п орбитальное квантовое число l может принимать значения от 0 до n-1, а каждому значению l соответствуют 2l+1 различных значений ml, то кратность вырождения уровней водорода
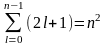 (1.6)
(1.6)
Так как при движении электрона в атоме существенны волновые свойства электрона, квантовая механика вообще отказывается от классического представления об электронных орбитах. Согласно квантовой механике, каждому энергетическому состоянию соответствует волновая функция, квадрат модуля которой определяет плотность вероятности обнаружения электрона в окрестности данной точки пространства.
Вероятность обнаружения электрона в различных частях атома различна. Электрон при своем движении как бы «размазан» по всему объему, образуя электронное облако, плотность (густота) которого характеризует вероятность нахождения электрона в различных точках объема атома. Квантовые числа п и l характеризуют размер и форму электронного облака, а квантовое число ml характеризует ориентацию электронного облака в пространстве.
Правилами отбора в квантовой механике называются условия, накладываемые на изменения квантовых чисел.
Для
гармонического осциллятора возможны
лишь переходы между соседними подуровнями,
т.е. переходы, удовлетворяющие
правилу отбора:
 .
Следовательно, энергия гармонического
осциллятора может изменяться только
порциями
.
Следовательно, энергия гармонического
осциллятора может изменяться только
порциями
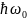 и гармонический осциллятор испускает
и поглощает энергию квантами.
и гармонический осциллятор испускает
и поглощает энергию квантами.
Квантово-механическое
решение задачи о квантовом осцилляторе
показывает, что имеется отличная от
нуля вероятность, обнаружить частицу
за пределами области
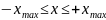 .
Cуществование
отличных от нуля значений вероятности
обнаружения частицы за пределами
потенциальной ямы объясняется возможностью
прохождения микрочастиц сквозь
потенциальный барьер.
.
Cуществование
отличных от нуля значений вероятности
обнаружения частицы за пределами
потенциальной ямы объясняется возможностью
прохождения микрочастиц сквозь
потенциальный барьер.
На
рис
5 приведена
квантовая плотность вероятности
обнаружения осциллятора при
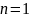 ,
имеющая конечные значения для
,
имеющая конечные значения для
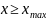 .
.
№11
1) Химические связи. Экспериментально доказано, что рентгеновские спектры тяжелых элементов не зависят от того, в состав какого химического соединения входит данный элемент. Отсюда следует, что силы, удерживающие атомы в молекуле, вызваны взаимодействием внешних электронов. Электроны внутренних оболочек при объединении атомов в молекулу остаются в прежних состояниях.
Ограничимся рассмотрением только двухатомных молекул. Различают два вида связи между атомами в молекуле. Один из них осуществляется в том случае, когда электроны в молекуле можно разделить на две группы, каждая из которых все время находится около одного из ядер. Электроны распределяются так, что около одного из ядер образуется избыток электронов, а около другого- их недостаток. Таким образом, молекула как бы состоит из двух ионов противоположных знаков, притягивающихся друг к другу. Связь этого типа называется гетерополярной (или ионной.). Примером молекул с гетерополярной связью могут служить NaCl, KBr, HCl и т.д.
Второй вид связи наблюдается в тех молекулах, в которых часть электронов движется около обоих ядер. Такая связь называется гомеополярной (или ковалентной, или атомной). Она образуется парами электронов с противоположно направленными спинами. Среди молекул этого типа следует различать молекулы с одинаковыми ядрами (H2 , N2 , O2) и молекулы с разными ядрами (например, CN). В молекулах первого рода электроны распределены симметрично. В молекулах второго рода имеется некоторая асимметрия в распределении электронов, благодаря чему молекулы приобретают электрический дипольный момент.
Энергия молекулы. Потенциальные поверхности и потенциальные кривые.
Простейшей молекулой с гомеополярной связью является молекула водорода. Вскоре после создания квантовой механики Гайтлер и Лондон (1927) предприняли успешную попытку квантовомеханического расчета основного состояния молекулы H2 . Им удалось решить уравнение Шредингера для системы, состоящей из двух протонов (ядер атома водорода) и двух электронов (рис.5.1).

Потенциальная энергия такой системы равна
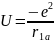
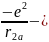
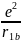
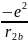 +
+
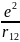 +
+
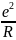 (1)
(1)
Ядра имеют массу, примерно в 2000 раз превышающую массу электрона. Поэтому они движутся гораздо медленнее электронов, и в первом приближении их можно считать неподвижными. В этом приближении уравнение Шредингера имеет вид.
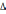 1ψ
+
2
ψ +
1ψ
+
2
ψ +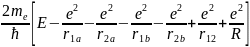 ψ=0 (2)
ψ=0 (2)
Здесь 1 –оператор Лапласа, содержащий координаты одного электрона, а 2 - оператор Лапласа, содержащий координаты другого электрона.

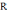 , т.е.
, т.е.
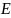 =
=
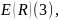 причем в случаях параллельной и
антипараллельной ориентации спинов
электронов характер этой зависимости
существенно различен (рис.2).
причем в случаях параллельной и
антипараллельной ориентации спинов
электронов характер этой зависимости
существенно различен (рис.2).

Образование
молекулы возможно лишь при сближении
атомов с антипараллельными спинами.
Асимптотическое значение
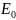 ,
к которому стремится энергия молекулы
при
,
к которому стремится энергия молекулы
при
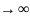 для обеих изображенных на рисунке
кривых, одинаково и равно сумме энергий
изолированных атомов.
для обеих изображенных на рисунке
кривых, одинаково и равно сумме энергий
изолированных атомов.
Аналогично обстоит дело и в случае других двухатомных молекул. Энергия, обусловленная электронной конфигурацией (электронная энергия), имеет минимум при некотором значении и изображается кривой такого же вида, как для водородной молекулы (см. кривую 1 на рис. 3).
В основном изменение энергетического запаса молекулы происходит, как и в атоме, в результате изменений в электронной конфигурации, образующей периферическую часть молекулы. Однако при заданной электронной конфигурации ядра молекулы могут различным образом колебаться и вращаться относительно общего центра масс. С этими видами движения связаны запасы колебательной и вращательной энергии, которые должны быть учтены в общем балансе. Введем обозначения:
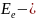 энергия,
обусловленная электронной конфигурацией
(электронная энергия);
энергия,
обусловленная электронной конфигурацией
(электронная энергия);
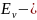 энергия,
соответствующая колебаниям молекулы
(колебательная или вибрационная энергия);
энергия,
соответствующая колебаниям молекулы
(колебательная или вибрационная энергия);
 –энергия, связанная с вращением молекулы
(вращательная или ротационная энергия).
–энергия, связанная с вращением молекулы
(вращательная или ротационная энергия).
В первом приближении отдельные виды молекулярных движений – движение электронов, колебание и вращение молекулы - можно считать независимыми друг от друга. Поэтому полную энергию молекулы можно представить в виде
E=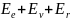 .
(3)
.
(3)
Из уравнения (2) волновая функция рассматриваемой системы определяется как
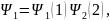 при перемене мест электронов, энергия
системы не меняется, а волновая функция
определяется
при перемене мест электронов, энергия
системы не меняется, а волновая функция
определяется
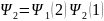 .
Волновая функция двух электронной
системы определяется как линейная
суперпозиция, выше приведенных,
произведений функций:
.
Волновая функция двух электронной
системы определяется как линейная
суперпозиция, выше приведенных,
произведений функций:
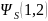 =
=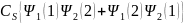 (4)
(4)
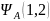 =
= (4a),
(4a),
где
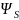 -
волновая функция, симметричная
относительно перемены мест координат
электронов,
-
волновая функция, симметричная
относительно перемены мест координат
электронов,
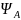 -
антисимметричная функция,
-
антисимметричная функция,
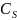 ,
,
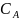 - нормировочные постоянные.
- нормировочные постоянные.
Ионная связь в молекулах.
Ковалентная связь в молекулах.
Энергия молекулы, потенциальные кривые.
Размеры молекул.
2) Волновая функция и ее свойства. Интенсивность волн де-Бройля в данной точке пространства связана с числом частиц, попавших в эту точку, о чем свидетельствуют опыты по дифракции микрочастиц. Поэтому волновые свойства микрочастиц требуют статистического (вероятностного) подхода к их описанию.
Для
описания поведения квантовых систем
вводится волновая
функция или
пси-фунция
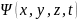 .
Правильную интерпретацию пси-функции
дал М.Борн в 1926г. Волновая функция
определяется таким образом, чтобы
вероятность
.
Правильную интерпретацию пси-функции
дал М.Борн в 1926г. Волновая функция
определяется таким образом, чтобы
вероятность
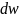 что частица находится в элементе объема
dv
была равна:
что частица находится в элементе объема
dv
была равна:
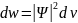 .
(1)
.
(1)
Физический
смысл имеет не сама функция
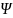 ,
а квадрат ее модуля
,
а квадрат ее модуля
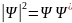 ,
которым задается интенсивность волн
де-Бройля (здесь
,
которым задается интенсивность волн
де-Бройля (здесь
 – функция, комплексно сопряженная с
).
Величина
– функция, комплексно сопряженная с
).
Величина
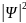 имеет смысл плотности
вероятности
имеет смысл плотности
вероятности
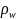 ,
а сама волновая функция
имеет смысл амплитуды
вероятности.
,
а сама волновая функция
имеет смысл амплитуды
вероятности.
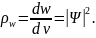 (2)
(2)
Условие нормировки вероятностей получается из того, что вероятность существования частицы где-либо в пространстве равна единице (интеграл вычисляется по всему бесконечному пространству).
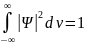 (3)
(3)
Волновая функция, характеризующая вероятность обнаружения действия микрочастицы в элементе объема должна быть: 1) конечной (вероятность не может быть больше единицы), 2)однозначной (вероятность не может быть неоднозначной величиной), 3)непрерывной (вероятность не может изменяться скачком).
Совокупность перечисленных требований носит название стандартных условий.
Волновая
функция позволяет вычислить средние
значения физических величин, характеризующих
данный микрообъект. Например, среднее
значение расстояния имеет вид
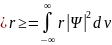 .
(4)
.
(4)
Волновая
функция удовлетворяет принципу
суперпозиции:
если система может находиться в различных
состояниях, описываемых волновыми
функциями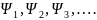 , то она может находиться в состоянии,
описываемом линейной комбинацией этих
функций
, то она может находиться в состоянии,
описываемом линейной комбинацией этих
функций
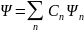 (5) (где - произвольные, вообще
говоря, комплексные числа).
(5) (где - произвольные, вообще
говоря, комплексные числа).
Сложение волновых функций (амплитуд вероятностей), а не вероятностей (определяемых квадратами модулей волновых функций) принципиально отличает квантовую теорию от классической статистической теории, в которой для независимых событий справедлива теорема сложения вероятностей.
№ 12
1)
Линейный
гармонический осциллятор
– система, совершающая одномерное
движение под действием квазиупругой
силы, является моделью, которая часто
используется при описании классических
и квантовых систем. Пружинный, физический
и математический маятники – примеры
классических гармонических осцилляторов.
Потенциальная энергия гармонического
осциллятора равна: U=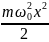 ,
где
,
где
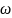 - собственная
частота колебаний осциллятора. m
– масса частицы.
- собственная
частота колебаний осциллятора. m
– масса частицы.
Гармонический
осциллятор в квантовой механике –
квантовый
осциллятор – описывается уравнением
Шредингера вида
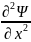 +
+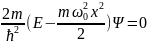 , где
, где
E - полная энергия осциллятора. Рис4
Собственные
значения энергии
для этого уравнения:
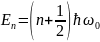 (n=0,1,2,…)
(n=0,1,2,…)
Таким
образом, энергия квантового осциллятора
квантуется
(может иметь лишь дискретные значения).
Уровни энергии расположены на одинаковых
расстояниях, равных
.
Минимальная энергия
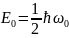 называется
энергией
нулевых колебаний. Существование
энергии нулевых колебаний – типично
квантовый эффект – прямое следствие
соотношение неопределенностей. Частица
в яме любой формы не может находиться
на ее дне, поскольку в нуль обращается
импульс частицы и его неопределенность,
а неопределенность координаты становится
бесконечной, что противоречит, в свою
очередь, условию пребывания частицы в
“потенциальной яме “.
называется
энергией
нулевых колебаний. Существование
энергии нулевых колебаний – типично
квантовый эффект – прямое следствие
соотношение неопределенностей. Частица
в яме любой формы не может находиться
на ее дне, поскольку в нуль обращается
импульс частицы и его неопределенность,
а неопределенность координаты становится
бесконечной, что противоречит, в свою
очередь, условию пребывания частицы в
“потенциальной яме “.
2) В опытах Франка и Герца было экспериментально доказано существование в атомах
стационарных состояний.
Электроны,
эмитированные катодом К, разгоняются
в области 1 под действием ускоряющей
разности потенциалов φ между катодом
и сеткой S
(рис2).
В
области 2 электроны проходят через пары
ртути и достигают анода А. Первое
возбужденное состояние атома ртути
имеет энергию 4,86 эВ. При увеличении
ускоряющего ускоряющего потенциала φ
до этой величины, соударения электронов
с атомами становятся неупругими: электрон
отдает кинетическую энергию атому,
возбуждая переход из основного
энергетического состояния в первое
возбужденное состояние (поглощение
энергии атомами ртути) –ток в установке
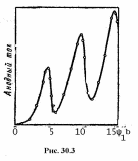
резко уменьшается (рис3).
При
дальнейшем
увеличении ускоряющего потенциала
φ, подобное
же поведение тока наблюдается при
энергиях, кратных
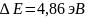 ,
когда электроны испытывают 2,3,4….
неупругих соударений.
,
когда электроны испытывают 2,3,4….
неупругих соударений.
Таким образом, в атоме действительно существуют стационарные состояния. Это является подтверждением первого постулата Бора.
Возбужденные
атомы ртути, переходя в основное
состояние, излучают кванты света с
длиной волны
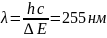 .
Это является
подтверждением второго постулата Бора.
.
Это является
подтверждением второго постулата Бора.
Аналогичные опыты были проведены и с другими атомами, которые также экспериментально подтверждают существование в атомах стационарных состояний. Отметим, что это свойство характерно не только атомам. Так, спектроскопические измерения доказывают, что квантование энергетических уровней имеет место в молекулах и в более сложных системах частиц.
№13
1) Одномерная “потенциальная яма “ с бесконечно высокими “стенками“ описывается потенциальной энергией вида
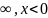
Рис1
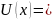 {0,
0
{0,
0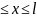 (1)
(1)
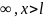
где
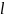 - ширина “ямы”, а энергия отсчитывается
от ее дна.
- ширина “ямы”, а энергия отсчитывается
от ее дна.
Уравнение Шредингера для стационарных состояний в пределах “ямы”:
+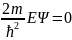 (2) или
+
(2) или
+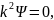 (3) где
(3) где
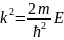 (4)
(4)
За
пределы “ямы” частица не проникает,
поэтому волновая функция вне “ямы”
равна нулю, следовательно, на границах
“ямы” непрерывная волновая функция
также должна обращаться в нуль: Ψ(0)=
Ψ .
(5)
.
(5)
Этим граничным условиям удовлетворяет решение уравнения Шредингера
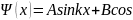 kx
(6) при B=0
и k=
kx
(6) при B=0
и k=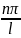 . Поскольку
,
. Поскольку
,
то
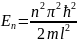 (n=1,2,3,…)
- собственные
значения энергии. (7)
(n=1,2,3,…)
- собственные
значения энергии. (7)
При
этом минимально возможное значение
энергии:
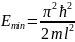 .
(7а)
.
(7а)
Таким
образом, энергия частицы в бесконечно
высокой потенциальной “яме” лишь
определенные дискретные значения, т.е.
квантуется.
Квантованные значения энергии
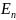 называются уровнями энергии, а число
n,
определяющее энергетические уровни
частицы. Называется главным
квантовым числом.
называются уровнями энергии, а число
n,
определяющее энергетические уровни
частицы. Называется главным
квантовым числом.
Собственные
волновые функции
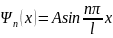 , c
учетом нормировки
, c
учетом нормировки
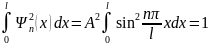 , будут иметь вид:
, будут иметь вид:
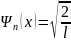
 (n=1,2,3,….).
(8)
(n=1,2,3,….).
(8)
На
рис2
изображены
графики собственных функций (а) и
плотность вероятности (б) обнаружения
частицы на разных расстояниях от стенок
ямы, определяемая выражением
 для n=1,2
и 3. Из рис2
следует,
например, в квантовом состоянии с n=2
частица не может находиться в середине
“ямы”, в то время как одинаково часто
может пребывать в ее левой и правой
частях. Такое поведение частицы указывает
на то, что представления о траекториях
частицы в квантовой механике несостоятельны.
для n=1,2
и 3. Из рис2
следует,
например, в квантовом состоянии с n=2
частица не может находиться в середине
“ямы”, в то время как одинаково часто
может пребывать в ее левой и правой
частях. Такое поведение частицы указывает
на то, что представления о траекториях
частицы в квантовой механике несостоятельны.
Из
выражения (7ф) вытекает, что энергетический
интервал между двумя соседними уровнями
равен
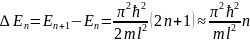 (9)
(9)
Например,
для электрона при размерах ямы l=10-1
м (свободные электроны в металле)
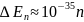 Дж
Дж
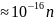 эВ, т.е. энергетические уровни расположены
столь тесно, что спектр практически
можно считать непрерывным. Если же
размеры ямы соизмеримы с атомными (l
эВ, т.е. энергетические уровни расположены
столь тесно, что спектр практически
можно считать непрерывным. Если же
размеры ямы соизмеримы с атомными (l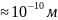 ),
то для электрона
),
то для электрона
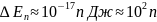 эВ , т.е. получаются дискретные значения
энергии (линейчатый спектр).
эВ , т.е. получаются дискретные значения
энергии (линейчатый спектр).
Кроме того, частица в потенциальной яме с бесконечно высокими стенками не может иметь энергию, меньшую чем минимальная энергия (7б), что соответствует принципу неопределенности. При очень больших значениях n дискретность сглаживается. Этот результат является частным случаем принципа соответствия Бора (1923г.), согласно которому законы квантовой механики должны при больших значениях квантовых чисел переходить в законы классической физики.
2) Абсолютно черное тело Как поглощательная, так и лучеиспускательная способности твердого тела зависят от частоты излучаемых или поглощаемых волн, от температуры тела, от его химического состава и состояния поверхности. Если тело полностью поглощает падающую на него энергию электромагнитного излучения при любой температуре и для всех частот, то такое тело называют абсолютно черным. Поглощательная способность абсолютно черного тела по определению равна единице .
Лучеиспускательная способность абсолютно черного тела зависит только от частоты и абсолютной температуры. Реальные тела не являются абсолютно черными. Достаточно хорошим приближением абсолютно черного тела являются сажа, платиновая чернь, черный бархат. Наиболее близкой моделью абсолютно черного тела является поверхность малого отверстия в непрозрачной стенке замкнутой полости.
Закон
Кирхгофа
отношение лучеиспускательной способности
тела к его поглощательной способности
не зависит от химического состава тела
и равно лучеиспускательной способности
абсолютно черного тела и является
функцией температуры и частоты
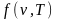 .
Этот закон был впервые установлен
Кирхгофом и носит его название, а функция
называется функцией Кирхгофа. Из закона
Кирхгофа следует, что, если
,
то
.
Этот закон был впервые установлен
Кирхгофом и носит его название, а функция
называется функцией Кирхгофа. Из закона
Кирхгофа следует, что, если
,
то
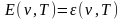 ,
если
,
если
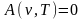 ,
то
,
то
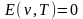 .
Следовательно, если тело не поглощает
при данной температуре в данном интервале
частот, то оно не может и излучать при
этой же температуре и этом же интервале
частот.
.
Следовательно, если тело не поглощает
при данной температуре в данном интервале
частот, то оно не может и излучать при
этой же температуре и этом же интервале
частот.
