1.Элементарная боровская теория водородного атома.

в ИНТЕРНЕТЕ НЕТ НОРМАЛЬНОЙ ИНФОРМАЦИИ

2. Нормальный эффект Зеемана

Простым или нормальным эффектом Зеемана называется расщепление спектральных линий на три подуровня, и качественно может быть объяснён классически. Если член взаимодействия мал (меньше тонкой структуры то есть ), нормальный эффект Зеемана наблюдается:

при переходах между синглетными термами ( );

при переходах между уровнями и ;

при переходах между уровнями и , поскольку не расщепляется, а расщепляется на три подуровня.

В сильных полях так же наблюдается расщепление на три подуровня, однако это может происходить вследствие эффекта Пашена — Бака (см. далее).

При нормальном эффекте Зеемана расщепление связано с чисто орбитальным или чисто спиновым магнитным моментами. Это наблюдается в синглетах He и в группе щелочноземельных элементов, а также в спектрах Zn, Cd, Hg.

И поляризация наблюдаются при изменении проекции магнитного момента на и , соответственно.

Несмотря на то, что Зееман изначально наблюдал в своих экспериментах именно простой эффект, в природе он встречается относительно редко.

Билет 3.

Стационарное уравнение Шредингера. Линейный гармонический осциллятор.

Одномерное стационарное уравнение Шрёдингера — линейное обыкновенное дифференциальное уравнение второго порядка вида

Где — постоянная Планка, — масса частицы, — потенциальная энергия, — полная энергия, — волновая функция. Для полной постановки задачи о нахождении решения надо задать также граничные условия, которые представляются в общем виде для интервала

Где — константы.

Линейным гармоническим осциллятором называется система, потенциальная энергия которой квадратично зависит от координаты:

Здесь m — масса частицы, а ω — собственная частота осциллятора. На рис. 11.1 зависимость (1)

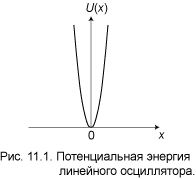
изображена графически. Кривая U(x) своей крутизной и бесконечно большой высотой напоминает потенциальную яму. Ниже мы увидим, что линейный осциллятор, действительно, проявляет некоторые свойства частицы в бесконечно высокой потенциальной яме. Например, он имеет бесконечное число дискретных уровней. Но в отличие от отвесных стенок ямы, потенциал осциллятора растёт плавно, и, как следствие, появляется некоторая вероятность обнаружить частицу достаточно далеко от начала координат. Плавная форма потенциала позволяет осциллятору при определённых условиях проявить свойства классической (не квантовой) частицы. Для этого достаточно, чтобы длина волны де Бройля была меньше характерных размеров области изменения потенциала. В случае потенциальной ямы, либо потенциального барьера, такая возможность полностью исключена, так как там потенциал меняется скачком в одной точке. Перейдём к количественному решению задачи.

Напишем одномерное уравнение Шредингера с потенциальной энергией (1):

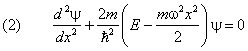
У него нет естественных граничных условий. Дискретные уровни энергии получаются как следствие ограниченности волновой функции.

Преобразуем уравнение (2): вместо координаты x введём безразмерный аргумент

и вместо E — безразмерную энергию осциллятора

Легко убедиться, что обратная величина подкоренного выражения в (3) равна произведению комптоновской длины волны электрона (1.3.1) и длины волны D = l/(2p) =c/w, соответствующей собственной частоте осциллятора. С принятыми обозначениями уравнение Шредингера принимает вид:

Здесь штрихами обозначено дифференцирование по координате y.

Квантовые свойства осциллятора имеют многочисленные приложения в атомной физике. Ниже мы рассмотрим два из них: влияние нулевых колебаний электромагнитного вакуума на функцию Планка и связанный с ними лэмбовский сдвиг метастабильного уровня атома водорода.

Квантовые числа. Принцип Паули

Квантовые числа — энергетические параметры, определяющие состояние электрона и тип атомной орбитали, на которой он находится.

Главное квaнтовое число n определяет общую энергию электрона и степень его удаления от ядра (номер энергетического уровня); оно принимает любые целочисленные значения, начиная с 1 (n = 1, 2, 3, . . .)

Орбитальное (побочное или азимутальное) квантовое число l определяет форму атомной орбитали. Оно может принимать целочисленные значения от 0 до n-1 (l = 0, 1, 2, 3,..., n-1). Каждому значению l соответствует орбиталь особой формы. Орбитали с l = 0 называются s-орбиталями,

l = 1 – р-орбиталями (3 типа, отличающихся магнитным квантовым числом m),

l = 2 – d-орбиталями (5 типов),

l = 3 – f-орбиталями (7 типов).

Магнитное квантовое число m определяет ориентацию орбитали в пространстве относительно внешнего магнитного или электрического поля. Его значения изменяются от +l до -l, включая 0. Например, при l = 1 число m принимает 3 значения: +1, 0, -1, поэтому существуют 3 типа р-АО: рx, рy, рz.

Спиновое квантовое число s может принимать лишь два возможных значения +1/2 и -1/2. Они соответствуют двум возможным и противоположным друг другу направлениям собственного магнитного момента электрона, называемого спином (от англ. веретено).

ПАУЛИ ПРИНЦИП, фундаментальный принцип квантовой механику согласно к-рому у системы тождественных элементарных частиц с полуцелым спином (фер-мионов) каждое квантовое состояние м. б. заполнено не более чем одной частицей. В. Паули сформулировал этот принцип, названный им принципом запрета, в январе 1925, незадолго до того, как была создана квантовая механика (1925-26), для объяснения наблюдаемых закономерностей в электронных спектрах атомов, помещенных в магн. поле. Согласно этой формулировке, в атоме не может существовать двух или более электронов, для к-рых значения всех четырех квантовых чисел n, l, mi, и ms одинаковы (см. Атом). В то время понятие спина еще не было введено, поэтому четвертое квантовое число не описывалось В. Паули никакой моделью. Он назвал связанное с ним св-во "характерной двузначностью квантовых свойств электрона, которую нельзя описать классически".

Австрийский физик Вольфганг Паули — один из нескольких европейских физиков-теоретиков, сформулировавших в конце 1920-х — начале 1930-х годов основные принципы и постулаты квантовой механики. Принцип, носящий его имя, является одним из основополагающих в этом разделе физической науки. Проще всего представить себе, в чем именно заключается принцип Паули, если сравнить электроны с автомобилями на многоярусной крытой стоянке. В каждый бокс помещается только одна машина, а после того, как все боксы на нижнем этаже стоянки заняты, автомобилям приходится в поисках свободного места заезжать на следующий этаж. Так же и электроны в атомах — на каждой орбите вокруг ядра их помещается не больше, чем там имеется «парковочных мест», а после того, как все места на орбите заняты, следующий электрон ищет себе место на более высокой орбите.

Далее, электроны ведут себя, условно говоря, так, будто они вращаются вокруг своей оси (то есть, обладают собственным моментом вращения, который в этом случае принято называть спином и который может принимать лишь два значения: +1/2 или –1/2). Два электрона с противоположным спином могут занимать одно место на орбите. Это, как если бы в один бокс помещались одновременно машина с правым рулем и машина с левым рулем, а две машины с одинаковым расположением руля не помещались. Вот почему в первом ряду периодической системы Менделеева мы видим всего два атома (водород и гелий): на нижней орбите отведено всего одно сдвоенное место для электронов с противоположным спином. На следующей орбите помещается уже восемь электронов (четыре со спином –1/2, и четыре со спином +1/2), поэтому во втором ряду таблицы Менделеева мы видим уже восемь элементов. И так далее.

Внутри стареющих звезд температура настолько высока, что атомы в основном находятся в ионизированном состоянии, и электроны свободно перемещаются между ядрами. И здесь снова срабатывает принцип запрета Паули, но уже в видоизмененной форме. Теперь он гласит, что в определенном пространственном объеме может одновременно находиться не более двух электронов с противоположным спином и определенными интервалами предельно допустимых скоростей. Однако картина резко изменяется после того, как плотность вещества внутри звезды превысит пороговое значение порядка 107 кг/м3 (для сравнения — это в 10 000 раз выше плотности воды; спичечный коробок такого вещества весит около 100 тонн). При такой плотности принцип Паули начинает выражаться в стремительном росте внутреннего давления в звезде. Это дополнительное давление вырожденного электронного газа, и его проявлением становится тот факт, что гравитационный коллапс старой звезды останавливается после того, как она сжимается до размеров, сопоставимых с размерами Земли. Такие звезды называют белыми карликами, и это последняя стадия эволюции звезд с массой, близкой к массе Солнца (см. Предел Чандрасекара).

Выше я описал действие запрета Паули применительно к электронам, но он действует и в отношении любых элементарных частиц с полуцелым спиновым числом (1/2, 3/2, 5/2 и т. д.). В частности, спиновое число нейтрона равно, как и у электрона, 1/2. Это значит, что нейтронам, как и электронам, требуется определенное «жизненное пространство» вокруг себя. Если масса белого карлика превышает 1,4 массы Солнца (см. Предел Чандрасекара), силы гравитационного притяжения заставляют протоны и электроны внутри звезды попарно объединяться в нейтроны. Но тогда нейтроны, подобно электронам в белых карликах, начинают производить внутренне давление, которое называется давлением вырожденного нейтронного газа, и в этом случае гравитационный коллапс звезды останавливается на стадии образования нейтронной звезды, диаметр которой сопоставим с размерами большого города. Однако при еще большей массе звезды (начиная примерно с тридцатикратной массы Солнца) силы гравитации сламывают и сопротивление вырожденного нейтронного газа, и звезды коллапсируют дальше, превращаясь в черные дыры.

Принцип запрета Паули представляет собой яркий пример закона природы нового типа, и по мере развития компьютерных технологий такие «неявные» законы будут неизбежно играть всё большую роль. Законы этого типа принципиально отличаются от законов классической физики, таких как законы механики Ньютона, — они не предсказывают, что произойдет в системе. Вместо этого они определяют, чего в системе не может произойти. Именно их биолог и структурный теоретик Харольд Моровиц (Harold Morowitz, р. 1927) назвал «правилами отсечения»: такие правила, в частности, принцип запрета Паули сводятся к тому, что при решении самых сложных и комплексных проблем (а расчет орбит электронов в сложных атомов к таковым, несомненно, относится) следует запрограммировать компьютер таким образом, чтобы он даже не рассматривал заведомо невозможные варианты решения. Тем самым такое правило отсекает от ствола возможных решений задачи заведомо мертвые ветви, оставляя лишь допустимые возможности для ее решения, благодаря чему время компьютерных расчетов сокращается до разумных пределов. Таким образом, правила, подобные принципу запрета Паули, становятся всё более важными, поскольку мы всё больше зависим от компьютеров в решении самых сложных и комплексных проблем.

Билет 4.

Спектральные серии атома водорода. Обобщенная формула Бальмера

Спектральные серии водорода — набор спектральных серий, составляющих спектр атома водорода. Поскольку водород — наиболее простой атом, его спектральные серии наиболее изучены. Они хорошо подчиняются формуле Ридберга:

,

где R = 109 677 см−1 — постоянная Ридберга для водорода, n′ — основной уровень серии.

Спектральные линии, возникающие при переходах на основной энергетический уровень, называются резонансными, все остальные — субординатными.

Серия Лаймана

Открыта Т. Лайманом[en] в 1906 году. Все линии серии находятся в ультрафиолетовом диапазоне. Серия соответствует формуле Ридберга при n′ = 1 и n = 2, 3, 4, …; линия Lα = 1216 Å является резонансной линией водорода. Граница серии — 911,8 Å.

Серия Бальмера

Открыта И. Я. Бальмером в 1885 году. Первые четыре линии серии находятся в видимом диапазоне и были известны задолго до Бальмера, который предложил эмпирическую формулу для их длин волн и на её основе предсказал существование других линий этой серии в ультрафиолетовой области. Серия соответствует формуле Ридберга при n′ = 2 и n = 3, 4, 5, …; линия Hα = 6565 Å, граница серии — 3647 Å.

Серия Пашена

Предсказана Ритцем в 1908 году на основе комбинационного принципа. Открыта Ф. Пашеном в том же году. Все линии серии находятся в инфракрасном диапазоне. Серия соответствует формуле Ридберга при n′ = 3 и n = 4, 5, 6, …; линия Pα = 18 756 Å, граница серии — 8206 Å.

Серия Брэккета

Открыта Ф. С. Брэккетом в 1922 году. Все линии серии находятся в ближнем инфракрасном диапазоне. Серия соответствует формуле Ридберга при n′ = 4 и n = 5, 6, 7, …; линия Bα = 40 522 Å. Граница серии — 14 588 Å.

Серия Пфунда

Открыта А. Г. Пфундом в 1924 году. Линии серии находятся в ближнем (часть в среднем) инфракрасном диапазоне. Серия соответствует формуле Ридберга при n′ = 5 и n = 6, 7, 8, …; линия Pfα = 74 598 Å. Граница серии — 22 794 Å.

Серия Хэмпфри

Открыта К. Д. Хэмпфри в 1953 году. Серия соответствует формуле Ридберга при n′ = 6 и n = 7, 8, 9, …; основная линия — 123 718 Å, граница серии — 32 823 Å.

Формула Бальмера

Для описания длин волн λ четырёх видимых линий спектра водорода И. Бальмер предложил формулу

где n = 3, 4, 5, 6; b = 3645,6 Å.

В настоящее время для серии Бальмера используют частный случай формулы Ридберга:

где λ — длина волны,

R ≈ 109737,3157 см−1 — постоянная Ридберга,

n — главное квантовое число исходного уровня — натуральное число, большее или равное 3.

Первые 4 линии серии находятся в видимом диапазоне, остальные — в ультрафиолетовом.